（浙江温州卷）2023年中考数学第三次模拟考试

2023年中考数学第三次模拟考试【浙江温州卷】

数学·参考答案

一、选择题

二、填空题

11．                 12．25°                      13．

14．                             15．                   16．1或或2

三、解答题

17．（1），；（2）

【解析】

【分析】

（1）先计算括号内的，再计算除法，然后把代入化简后结果，即可求解；

（2）分别求出两个不等式，即可求解．

【详解】

解∶（1）

当时，原式；

（2），

解不等式①得：，

解不等式②得：，

∴不等式组的解集为．

【点睛】

本题主要考查了分式的化简求值，解一元一次不等式组，熟练掌握相关运算法则是解题的关键．

18．(1)跳绳和毽子的单价分别是8元，5元

(2)当购买跳绳450根，毽子150个时，花费最少

【解析】

【分析】

（1）设毽子的单价为x元，则跳绳的单价为元，然后根据用800元购买的跳绳个数和用500元购买的键子数量相同，列出方程求解即可；

（2）设学校购买跳绳m根，则购买毽子个，花费为W，然后求出W关于m的关系式，利用一次函数的性质求解即可．

(1)

解：设毽子的单价为x元，则跳绳的单价为元，

由题意得：，

解得，

经检验，是原方程的解，

，

∴跳绳和毽子的单价分别是8元，5元，

答：跳绳和毽子的单价分别是8元，5元；

(2)

解：设学校购买跳绳m根，则购买毽子个，花费为W，

由题意得，

∵跳绳的数量不少于毽子数量的3倍，跳绳的数量不多于460根，

∴，

∴，

∵，

∴W随着m的增大而增大，

∴当m=450时，W有最小值，

∴当购买跳绳450根，毽子150个时，花费最少．

【点睛】

本题主要考查了分式方程的应用，一次函数的应用，解题的关键在于能够正确理解题意列出相应的式子求解．

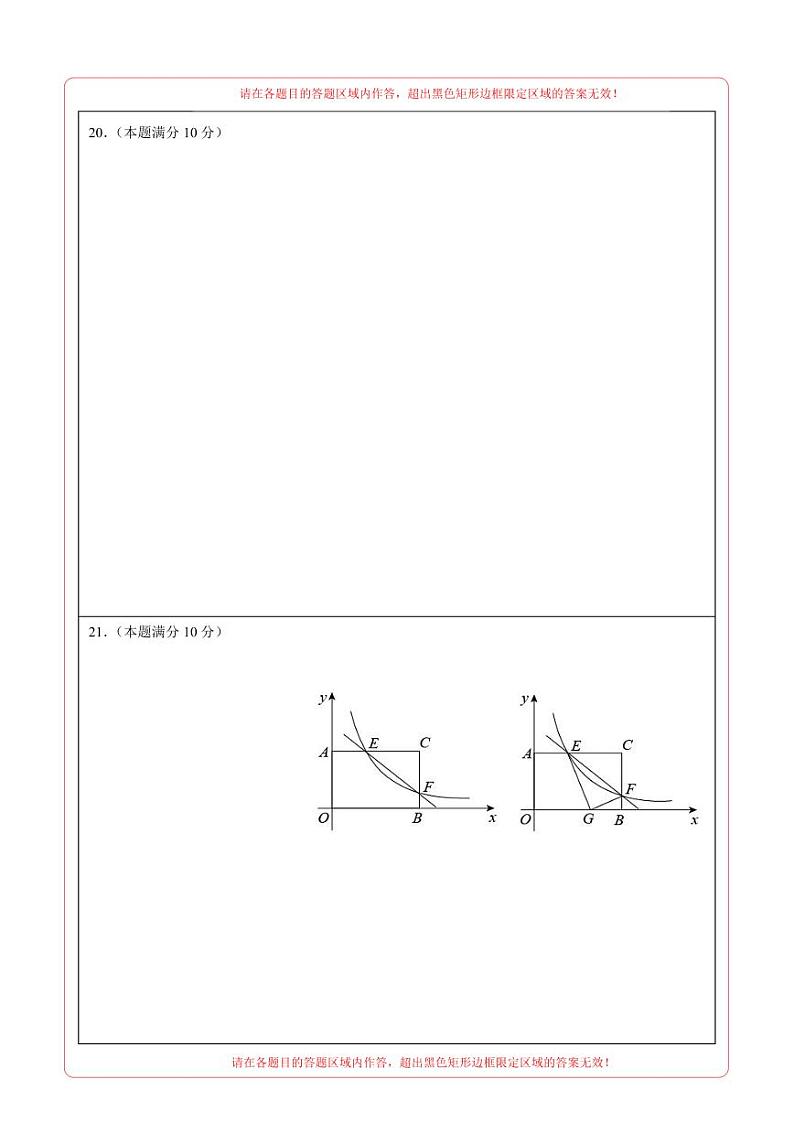
19．(1)点D到OE的距离约为0.6米

(2)OA的长约是4米

【解析】

【分析】

（1）过D作DF⊥AE于F， 在直角三角形中，通过解三角函数即可求解；

（2）分别用OC=CH+OH=O.8+AO+0.6，OC=BC+OB=2.4+，列出等式，求出OA即可．

(1)

解：过D作DF⊥AE于F，

∵AD=1，DF⊥AE

∴

点D到OE的距离约为0.6米

(2)

过D作DH⊥OC于H，则四边形AHCF是矩形，

在Rt△AOB中，∠ABO=53°

∴∠BAO=37°，

∴

∵从C处沿C0方向走4步到达点B处，，已知现测学生的步长为0.6米.

∴BC=2.4米

∴OC=BC+OB=2.4+

∵AD=1，DF⊥AE

∴

∵∠DCO=45°

∴CH=DH=OF=0.8+AO

∵四边形DHOF是矩形

∴OH=DF=0.6

∴OC=CH+OH=O.8+AO+0.6

∴2.4+=O.8+AO+0.6

∴AO=4MI米

答：匾额悬挂的高度是4米．

【点睛】

本题考查了解直角三角形的应用-仰角俯角问题，解答本题的关键是根据仰角构造直角三角形，利用三角函数求解．

20．(1)43，42.5，55%，65%，八年级，理由见解析

(2)能

(3)

【解析】

【分析】

（1）由平均数、众数、中位数的定义求解即可，再由两个年级的优秀率进行说明即可；

（2）先求出样本合格率，再由参加此次测试活动的总人数乘以合格率即可；

（3）画树状图，共有20种等可能的结果，两人在同一年级的结果有8种，再由概率公式求解即可．

(1)

解：（1）表中  43  ，  42.5 ，  55%  ，  65%  ．

从表中优秀率看，八年级样本优秀率高于七年级，因此估计该中学八年级学生的优秀率高，所以用优秀率评价，估计八年级学生掌握党史知识较好．（答案不唯一，合理即可）

(2)

解：∵样本合格率为，

∴估计总体的合格率大约为，

∴估计参加测试的两个年级合格学生约为（人），

∴估计参加此次测试活动成绩合格的学生人数能超过1000．

(3)

解：七年级满分有2人，记为，，八年级满分有3人，记为，，，

由列表可知，共有20种等可能的结果，其中两人在同一年级的结果有8种，

∴两人在同一年级的概率为．

【点睛】

本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．也考查了统计图和统计表．

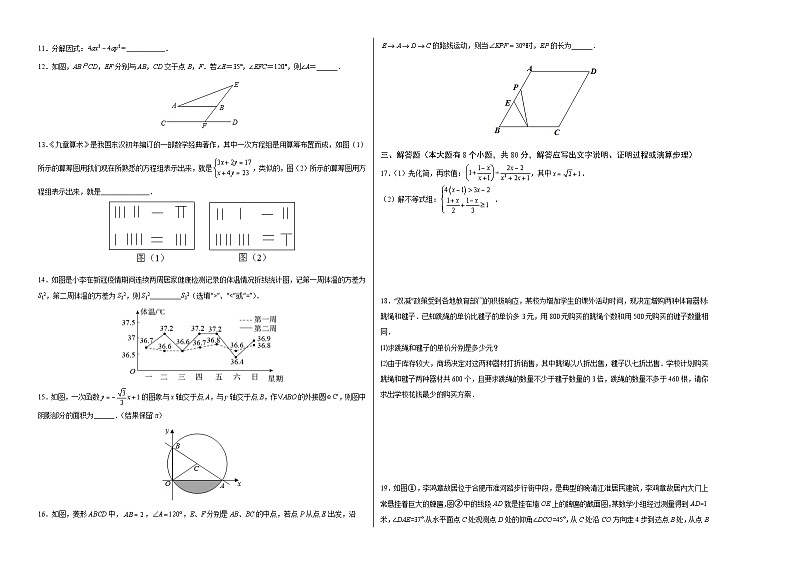
21．(1)(2，3)

(2)

(3)

【解析】

【分析】

（1）求出点F的坐标，进而求出反比例函数的表达式，即可求解；

（2）由CF=BC-BF，CE=AC-AE，求出CF、CE，即可求解；

（3）证明△EHG∽△GBF，即可求解．

(1)

解：∵OB=4，OA=3，

∴点A、B、C的坐标分别为：（0，3）、（4，0）、（4，3），

点F运动到边BC的中点时，点F（4，），

将点F的坐标代入y=并解得：k=6，

故反比例函数的表达式为：y=，

当y=3时，x==2，故E(2，3)，

故答案为：(2，3)；

(2)

解：∵F点的横坐标为4，点F在反比例函数上，

∴F（4，），

∴CF=BC-BF=3-=，

∵E的纵坐标为3，

∴E（，3），

∴CE=AC-AE=4-=

在Rt△CEF中，tan∠EFC==；

(3)

解：如图，由（2）知，CF=，CE=，

=，

过点E作EH⊥OB于H，

∴EH=OA=3，∠EHG=∠GBF=90°，

∴∠EGH+∠HEG=90°，

由折叠知，EG=CE，FG=CF，∠EGF=∠C=90°，

∴∠EGH+∠BGF=90°，

∴∠HEG=∠BGF，

∵∠EHG=∠GBF=90°，

∴△EHG∽△GBF，

∴，

∴，

∴BG=．

【点睛】

本题考查的反比例函数综合运用，涉及到一次函数的性质、三角形相似、解直角三角形等，综合性强，难度适中．

22．(1)见解析

(2)①见解析；②

【解析】

【分析】

（1）连接OD，由垂径定理得到AB垂直平分CD，所以PC＝PD，因为PD是⊙O切线，所以得到∠ODP＝90°，因为OC＝OD，得到∠OCD＝∠ODC，通过等量代换，可以算得∠OCP＝90°，即OC⊥CP，又OC是半径，从而证明PC是⊙O切线；

（2）①利用AB⊥CD，得到∠ECP+∠MPO＝90°，又OC⊥PC，则∠OCD+∠ECP＝90°，证得∠MPO＝∠OCD，又OM平分∠COP，得到∠CON＝∠MOP，从而得到△OMP∽△ONC；

②利用△OMP∽△ONC，得到∠CNO＝∠OMP，利用等角的补角相等，得到∠CNM＝∠CMO，所以CM＝CN＝10，过C作CG⊥MN于G，解直角△CMG，得到∠CMG的三角函数值，在直角三角形CMO中，因为CM＝10，tan∠CMO＝2，从而求得CO和OM的值，ON即可求．

(1)

连接OD，如图1，

∵PD为⊙O切线，

∴∠ODP＝90°，

∵AB⊥CD，且AB为⊙O直径，

∴AB垂直平分CD，

∴PC＝PD，

∴∠PCD＝∠PDC，

又∵OC＝OD，

∴∠OCD＝∠ODC，

∴∠OCP＝∠OCD+∠PCD＝∠ODC+∠PDC＝90°，

∴OC⊥PC，

∴PC为⊙O的切线；

(2)

①∵AB⊥CD，

∴∠CEP＝90°，

∴∠ECP+∠MPO＝90°，

又∠OCD+∠ECP＝90°，

∴∠MPO＝∠OCD，

又OM平分∠COP，

∴∠CON＝∠MOP，

∴△OMP∽△ONC；

解：②过C作CG⊥OM于G，

∵△OMP∽△ONC，

∴∠CNO＝∠OMP，

∵180°﹣∠CNO＝180°﹣∠OMP，

∴∠CMO＝∠CNM，

∴CM＝CN＝10，

∵CG⊥MN，

∴NG＝MG＝，

∴，

∴tan∠CMN＝，

又在Rt△COM中，

tan∠CMN＝，

∴OC＝2CM＝20，

∴，

∴．

【点睛】

本题考查圆的综合问题，涉及到切线的判定及其性质、垂径定理、相似三角形的判定及其性质、勾股定理解直角三角形等等，解题的关键是熟练运用所学知识和已知条件解三角形．

23．(1)抛物线对称轴为直线，与轴的交点坐标为和

(2)①和；②抛物线的解析式为，抛物线与抛物线两个顶点的距离为

(3)1或5

【解析】

【分析】

（1）将代入抛物线的解析式，再根据对称轴的计算公式可求出对称轴，然后求出时，的值，由此即可得与轴的交点坐标；

（2）①将抛物线的解析式改写成，令求出的值，再代入解析式求出的值，由此即可得；

②设抛物线的解析式为，将点和代入求出的值，由此即可得抛物线的解析式，再分别求出抛物线与抛物线的顶点坐标，由此即可得两个顶点的距离；

（3）根据抛物线的顶点的纵坐标的绝对值等于2即可得．

(1)

解：当时，，

则抛物线对称轴为直线，

当时，，解得或，

则抛物线与轴的交点坐标为和．

(2)

解：①将抛物线的解析式改写成，

令，

解得或，

当和时，，

则两个定点的坐标为和；

②由（2）①可知，这两个定点所在直线为，

则可设抛物线的解析式为，

将点和代入得：，

解得，

则抛物线的解析式为，

抛物线的顶点坐标为，

抛物线的顶点坐标为，

又因为，

所以抛物线与抛物线两个顶点的距离为．

(3)

解：因为（2）中抛物线的顶点到轴的距离为2，且抛物线的顶点坐标为，

所以，

解得或，均符合题意，

故的值为1或5．

【点睛】

本题考查了二次函数的图象与性质、一元二次方程的应用等知识点，熟练掌握二次函数的图象与性质是解题关键．

24．(1)见解析；

(2)AE＝CF，证明见解析；

(3)5

【解析】

【分析】

（1）证明△DAE≌△DCF（ASA），可得结论；

（2）证明△DAE≌△DCF（ASA），可得结论；

（3）如图4中，连接AC，取AC的中点O，连接OE，OD．证明∠AED＝∠DEC＝45°，AE＝AF，勾股定理求得EF，由DF＝3，得到答案

(1)

证明：如图1中，

∵四边形ABCD是正方形，

∴DA＝DC，∠A＝∠ADC＝∠DCB＝∠DCF＝90°，

∵DE⊥DF，

∴∠EDF＝∠ADC＝90°，

∴∠ADE＝∠CDF，

在△DAE和△DCF中，

，

∴△DAE≌△DCF（ASA），

∴AE＝CF．

(2)

解：AE＝CF

理由如下：如图2中，

∵四边形ABCD是正方形，

∴DA＝DC，∠DAB＝∠ADC＝∠DCB＝90°，

∵DE⊥DF，

∴∠EDF＝∠ADC＝90°，

∴∠ADE＝∠CDF，

∵AE⊥EF，

∴∠AEF＝90°，

∴∠DAE+∠DCE＝360°－∠AEF－∠ADC＝180°，

∵∠DCF+∠DCE＝180°，

∴∠DAE＝∠DCF，

在△DAE和△DCF中，

∴△DAE≌△DCF（ASA），

∴AE＝CF．

(3)

解：如图4中，连接AC，取AC的中点O，连接OE，OD．

∵四边形ABCD是正方形，

∴OA＝OC＝AC＝BD＝OD，∠ADC＝90°，∠ACD＝45°，AD＝CD

∵AE⊥EC，

∴∠AEC＝∠ADC＝90°，

∴ △AEC是直角三角形

∴OE＝AC，

∴OD＝OA＝OC＝OE

∴A，E，C，D四点共圆，

∴∠AED＝∠ACD＝45°，

∴∠AED＝∠DEC＝45°，

∵AE⊥AF，

∴∠EAF＝90°，

∴∠AEF＝∠AFE＝45°，

∴AE＝AF＝，

∴EF＝＝2，

∵DF＝3，

∴DE＝EF +DF＝5，

【点睛】

本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，四点共圆，圆周角定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用建模的思想思考问题，属于中考常考题．