2023届重庆市璧山区中考数学阶段性适应模拟试题（一模）含解析

2023届重庆市璧山区中考数学阶段性适应模拟试题（一模）

（全卷共五个大题，满分150分，考试时间120分钟）

参考公式：抛物线的顶点坐标为，对称轴为 ．

一、选择题：（本大题12个小题，每小题4分，共48分）下面每个小题的选项中只有一个选项是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

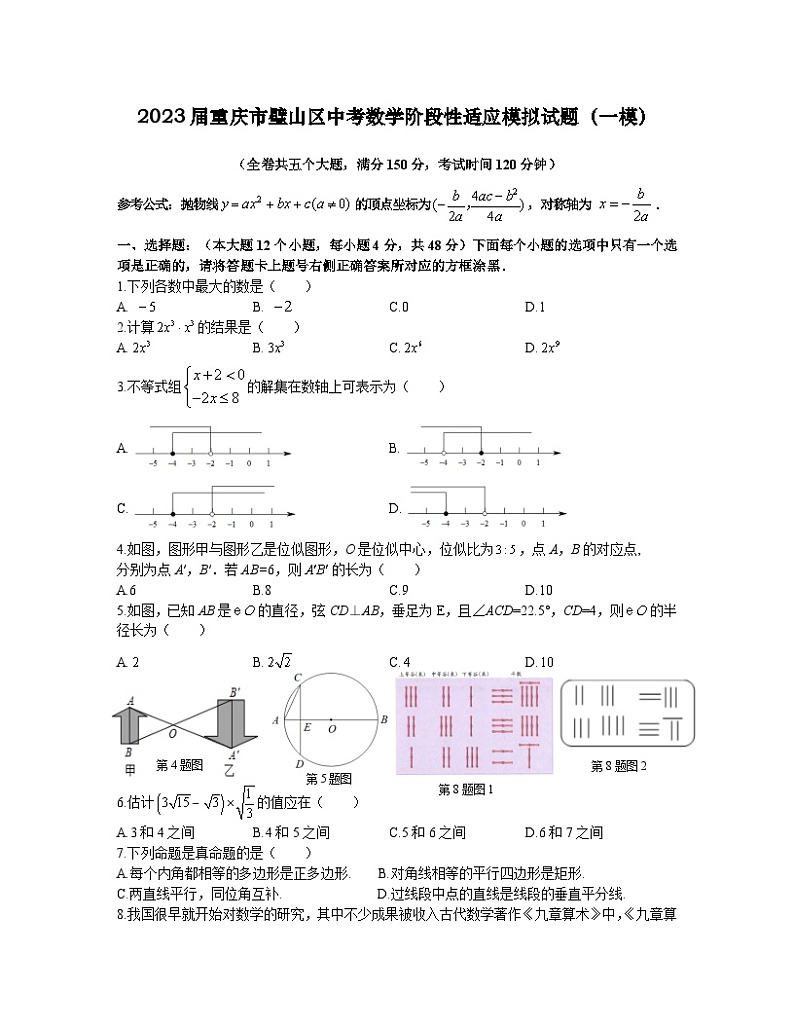
1.下列各数中最大的数是（    ）

A.     B.     C.0     D.1

2.计算的结果是（    ）

A.    B.    C.    D.

3.不等式组的解集在数轴上可表示为（    ）

A.    B.

C.    D.

4.如图，图形甲与图形乙是位似图形，O是位似中心，位似比为，点A，B的对应点,

分别为点A′，B′．若AB=6，则的长为（    ）

A.6     B.8     C.9     D.10

5.如图，已知AB是的直径，弦CD⊥AB，垂足为E，且∠ACD=22.5°，CD=4，则的半径长为（    ）

A.     B.    C.     D.

6.估计的值应在（    ）

A.3和4之间   B.4和5之间   C.5和6之间   D.6和7之间

7.下列命题是真命题的是（    ）

A.每个内角都相等的多边形是正多边形.    B.对角线相等的平行四边形是矩形.

C.两直线平行，同位角互补.              D.过线段中点的直线是线段的垂直平分线.

8.我国很早就开始对数学的研究，其中不少成果被收入古代数学著作《九章算术》中，《九章算术》的“方程”一章中，有许多关于一次方程组的内              容，这一章的第一个问题译成现代汉语是这样的： “上等谷3束，中等谷2束，下等谷1束，可得粮食39斗；上等谷2束，中等谷3束，下等谷1束，可得粮食34斗；上等谷1束，中等谷2束，下等谷3束，可得粮食26斗.问上、中、下三等谷每束各可得粮食几斗？”如图1的算筹代表了古代解决这个问题的方法，设每束上等谷、中等谷、下等谷各可得粮食x斗、y斗、z斗，则可列方程组为：类似地，图2所示的算筹我们可以表示为（    ）

 A.  B.  C. D.

9.小明和爸爸从家里出发，沿同一路线到图书馆，小明匀速跑步先出发，2分钟后，爸爸骑自行车出发，匀速骑行一段时间后，在途中商店买水花费了5分钟，从商店出来后，爸爸的骑车速度比他之前的骑车速度增加60米/分钟，结果与小明同时到达图书馆.小明和爸爸两人离开家的路程s（米）与小明出发的时间t（分钟）之间的函数图像如图所示，则下列说法错误的是（    ）

A.a=17.         B.小明的速度是150米/分钟.

C.爸爸从家到商店的速度是200米/分钟.  D.t=9时，爸爸追上小明.

10. 如图，在正方形ABCD中，将边BC绕点B逆时针旋转至点BC′，若∠CC′D=90°，CC′=2，则线段BC′的长度为（    ）

A.2     B.     C.    D.

11.已知的不等式组有且只有4个整数解，并且使得关于y的分式方程的解为整数，则满足条件的所有整数m的个数有（     ）

A.1个     B.2个    C.3个    D.4个

12.定义：如果代数式（是常数）与（是常数），满足，，，则称这两个代数式A与B 互为“同心式”，下列四个结论：

（1）代数式：的“同心式”为；

（2）若与互为“同心式”，则的值为1；

（3）当时，无论x取何值，“同心式”与的值始终互为相反数.

（4）若A、B互为“同心式”，有两个相等的实数根，则.

  其中，正确的结论有（    ）个

A.1个    B.2个    C.3个    D.4个

二、填空题：（本大题4个小题，每小题4分，共16分）请将每小题的答案直接填在答题卷中对应的横线上．

13.计算：=                .

14.现有4张正面分别标有数字的不透明卡片，它们除了数字外其余完全相同，将它们背面朝上洗均匀，随机抽取一张，将该卡片上的数字记为m，放回后再洗匀并随机抽取一张，将该卡片上的数字记为n，则满足方程mx+n=0的解是负数的概率为               . 

15.如图，矩形ABCD的两条对角线相交于点O，．以点A为圆心，AD长为半径画弧，此弧恰好经过点O，并与AB交于点E，则图中阴影部分的面积为            ．

16.疫情隔离期间，为了降低外出感染风险，各大商场开通了送货到小区的便民服务，某商场推出适合大多数家庭需要的A、B、C三种蔬菜搭配装袋供市民直接选择．其中，甲种搭配每袋装有3千克A，1千克B，1千克C；乙种搭配每袋装有1              千克A，2千克B，2千克C．甲、乙两种袋装蔬菜每袋成本价分别为袋中A、B、C三种蔬菜的成本价之和．已知A种蔬菜每千克成本价为2.4元，甲种搭配每袋售价为26元，利润率为30%，乙种搭配的利润率为20%．若这两种袋装蔬菜的销售利润率达到21%，则该商场销售甲、乙两种袋装蔬菜的数量之整数比是            ．（）

三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卷中对应的位置上．

17. 计算：  

18.  如图，在平行四边形ABCD中，．

（1）用尺规完成以下基本作图：作∠BAD的平分线交 BC于点E，在DA上截取 DF，使（保留作图痕迹，不写作法）；

（2）在(1)所作的图形中，连接EF，求证：四边形ABEF是菱形．请补全下面的证明过程.

证明：∵四边形ABCD为平行四边形，

∴且，

∵，

∴，

∴          ①           .           

∴四边形ABEF是平行四边形，

∵，

∴           ②            ．

∵AE平分∠BAF，

∴          ③           ，

∴．  

∴          ④            ，

∴四边形ABEF是菱形．

四、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡（卷）中对应的位置上．

19. 某省为了举办一场大型活动，特向大学召集志愿者.在志愿者招募之时，甲、乙两所大学就积极组织了志愿者选拔活动，对报名的志愿者进行现场测试，现从两所大学参加测试的志愿者中分别随机抽取了20名志愿者的测试成绩进行整理和分析（成绩得分用x表示，满分100分，共分成五组：A．，B．，C．，D．，E．），下面给出了部分信息：

信息1：甲校20名志愿者的成绩在D组的数据是：90，91，91，92．

信息2：乙校20名志愿者的成绩成绩是：82，89，80，85，88，89，87，96，96， 99，96，92，91，93，96，97，98，92，94，100．

信息3：        

根据以上信息，解答下列问题：

（1）由上表填空：a＝___，b＝___，＝ ___°．

（2）你认为哪个学校的志愿者测试成绩较好，请说明理由（写出一条即可）．

（3）若甲校有200名志愿者，乙校有300名志愿者参加了此次侧试，估计此次参加测试的志愿者中，成绩在90分以上的志愿者有多少？

20.   如图1是2022年北京冬奥会首钢滑雪大跳台，曲线的设计灵感来自敦煌“飞天”飘 带，又名“雪飞天”，它是世界上首例永久性保留和使用的滑雪大跳台场馆．如图2，              为测量“雪飞天”的高度，测得大跳台跨度AB为140m，出发区CD为20m，且，AD为大跳台钢支架，在点A处测得点D的仰角∠DAB＝75°，在点C处测得点B的俯角∠ECB＝30°．（测角仪的高度忽略不计）

（1）求大跳台出发区CD距离地面AB的高度．（结果精确到1m；参考数据： ，，，）

（2）据了解，“雪飞天”需要造雪，分别用雪枪和雪炮来满足对于雪量和雪质的不同要求，雪炮出雪量大，适合室外滑雪场快速铺雪，雪枪造雪分布比较平均，相对造雪量比较小．若每台雪枪每小时出雪量比雪炮少，且一台雪枪出雪所用的时间与一台雪炮出雪所用的时间相等．求每台雪枪和雪炮每小时的出雪量．

21.如图，一次函数与反比例函数交于点，点C与点A关于原点对称.

（1）求一次函数和反比例函数的解析式，并在平面直角坐

标系中画出这两个函数的图象；

（2）求的面积；

（3）直接写出不等式的解集.

22.五一期间，璧山区丁家街道天天农家乐的草莓和枇杷相继成熟，为了吸引更多游客 走进乡村，体验采摘乐趣，天天农家乐推出采摘草莓和采摘枇杷两种方式：采摘1公斤草莓的费用比采摘1公斤枇杷的费用多15元，采摘2公斤草莓和1公斤枇杷的费用共90元。

（1）求采摘1公斤草莓和1公斤枇杷的费用分别是多少元？

（2）根据去年采摘情况表明，平均每天采摘草莓30公斤，采摘枇杷20公斤.天天 农家乐决定今年采摘枇杷的价格保持不变，采摘草莓的价格下调，采摘草莓的费用每降价3元，采摘草莓的数量会增加2公斤.天天农家乐要想平均每天的收益为1386元，请问采摘草莓每公斤应降价多少元？

23.已知一个四位自然数,它的各个数位上的数字均不为0,且满足千位数字与百位数 字的和等于十位数字与个位数字的和，则称这个数为“和对称数”，将这个四位自然              数N的千位数字和百位数字互换，十位数字和个位数字互换，得到,规定              .

例如：N=4536, ∵4+5=3+6,∴4536是“和对称数”， .

    N =2346,  ∵, ∴2346不是“和对称数”.

（1）请判断2451、3972是不是“和对称数”，并说明理由．若是，请求出对应的F（N）的值．

（2）已知A,B均为“和对称数”，其中,  （其，且均为整数），令，当k能被77整除时，求出所有符合条件的A的值.

24.如图，在平面直角坐标系xOy中，抛物线与x轴交于点，与y轴交于点．

（1）求抛物线的解析式；

（2）如图1，连接AC，点D为线段AC下方抛物线上一动点，过点D作DE∥y 轴交线段AC于E点，连接EO，记△ADC的面积为S1，△AEO的面积为S2，求S1﹣S2的最大值及此时点D的坐标；

（3）如图2，在(2)问的条件下，将抛物线沿射线CB方向平移个单位长度得到新抛物线，动点M在原抛物线的对称轴上，点N为新抛物线上一点，直接写出所有使得以点A、D、              M、N为顶点的四边形是平行四边形的点N的坐标，并把求其中一个点N的坐标的过程写出来．

25.在ΔABC中，AB = AC,∠ABC=30°,点D是边AB上的一动点，点F是边CD上的动 点,连接AF并延长至点E,交BC于G,连接BE，∠AFC=60°,且∠E+∠BDF=180°，

（1）如图1，若，，求的长；

（2）如图2，若D是AB的中点，连接DE、BF，求证：；

（3）如图3，在(2)问的条件下，将ΔBDE绕点B顺时针旋转，旋转中的三角形记 为,取的中点为M,连接CM.当CM取最大时，将ΔADF沿直线CM翻              折，得到,直接写出的值.

答案解析

一、选择题：（本大题12个小题，每小题4分，共48分）

DCADBC BADDBC

二、填空题：（本大题4个小题，每小题4分，共16分）

13.   14.    15.    16.7:45

三、解答题：（本大题9个小题，17、18每小题8分，19至25每小题10分，共86分）

17. （1）解：原式

（2）解：原式

18. （1）

（2）①AF=BE;②;③；

④AB=BE

19.  解（1）甲校EE组20×45％=9(人)，则第101，11个数据分别为91，92，

则，

乙校：96出现4次最多，则b=96，

甲校C组：20−4−9−20×(5％+5％)=5，则，

故91.5，96，90；

（2）乙校志愿者较好．

理由如下：

∵甲、乙两校的平均数虽然相同，但是乙校的中位数、众数均比甲校的大；或甲校的方              差为36.6，乙校的方差是31.4，而，

∴乙校的成绩较为稳定，∴乙校志愿者测试成绩较好；

（3）根据题意得：（人），

答：成绩在90分以上的共有315人．

20.   （1）如解图，过点D，C分别作AB的垂线，垂足分别为F，G，则四边形CDFG 是 矩形．

∴FG＝CD＝20m，CG＝DF，．

∴∠CBG＝∠ECB＝30°．

在Rt△BCG中，，

∴．

在Rt△ADF中，∠DAF＝75°，，∴．

又∵AF＋FG＋BG＝AB，AB＝140m，∴．解得DF≈60．

答：大跳台出发区CD距离地面AB的高度约为60m．

（2）设每台雪炮每小时的出雪量为，则每台雪枪每小时的出雪量为．

根据题意，得，解得x＝60．

经检验，x＝60是原方程的解，且符合题意．∴60－40＝20（）．

答：每台雪炮每小时的出雪量为，每台雪枪每小时的出雪量为．

21.  解析：（1），

（2）

法1：

法2：

法3：

法4：过点C作MC//AB，可得，则点，

（3）

22.  解 (1)设采摘1公斤草莓和1公斤枇杷的费用分别是元，根据题意得，

,解得：

答：采摘1公斤草莓的费用是35元，采摘1公斤枇杷的费用是20元.

(2) 设采摘草莓每公斤应降价元，根据题意，得：

解得（舍）

答：采摘草莓每公斤应降价6元.

23.  解：（1）3972不是“和对称数”，  ∵3+924, ∴3972不是“和对称数”.

2451是“和对称数”， ∵2+4=5+1,∴2451是“和对称数”，

.

（2）

,

，

∵A,B均为“和对称数”， ∴，

为整数

且为整数，且为整数，

当时，，A=3746

当时，，，A=4756,6776

当时，，，A=5766,7786

当时，，A=8796

综上，A的值为3746，4756，6776，5766,7786，8796

24.   解：（1）

（2）如图，延长交轴于点，

设直线的函数表达式为，

，，，解得，直线的函数表达式为 ，

设，其中，

，，，

，

，

，

当时，取得最大值，最大值为1，此时点的坐标为；

（3），，，抛物线沿射线方向平移个单位长度，

抛物线向右平移个单位长度，向上平移3个单位长度，

平移后的抛物线解析式为，

点M在原抛物线对称轴上，设点

当以AD为对角线时，，即，

点N为新抛物线上一点，

综上所述，点N的坐标为，，

25.  解：（1）如图1，过点E作EM⊥AB交于点M,

∵在ΔABC中，AB=AC,∠ABC=30°,∴∠BAC=120°，

BC=AB=4,∴AB=AC=4，∠E+∠BDF=180°，

∴∠EFD+∠EBD=180°，∠EFD=∠AFC=60°，∴∠EBD=120°，

在RtΔEBM中,∠EBM=∠180°-∠EBD=60°,BE=2,EM⊥BM,∴BM=1,EM=,在 RtΔAEM中,∠AME=90°,EM=,AM=5，∴AE=

（2）过点B作∠FBH=120°交FE延长线于点H,

∠EFD=∠AFC=60°，∴∠EBD=120°，

∠ADC+∠BDC=180°,∠BDC+∠BEA=180°, ∴∠ADC=∠BEA

在ΔADC和ΔBEA中，AB=AC,∠BAC=∠ABE=120°，

∴ΔADC≌ΔBEA(AAS) ，∴AD=BE， AD=BD,∴BD=BE，

∠EBD=∠FBH=120°，∴∠HBE=∠FBH，

∠E+∠BDF=180°，∠BEF+∠BEH=180°，∴∠BEH =∠BDF，∴ΔBEH ΔBDF (ASA)

∴EH=DF, BH=BF, ∴ΔBDH为等腰三角形，∴HF=BF,

∴FH=EF+EH=EF+DF=BF

 (3)

提示：当C、B、M三点共线时，CM最大