人教版数学八年级下册期末素质检测模拟试题（学校自测）2

这是一份人教版数学八年级下册期末素质检测模拟试题（学校自测）2，共12页。试卷主要包含了、单选题，、填空题，、解答题等内容，欢迎下载使用。
 人教版数学八年级下册期末素质检测模拟试题（学校自测）2 一 、单选题（本大题共15小题，共45分）1.（3分）下列运算中正确的是A.  B.
C.  D. 2.（3分）一次函数为常数且的图象如图所示，则使成立的的取值范围为
 A.  B.  C.  D. 3.（3分）下列各组数中，能作为直角三角形的三边长的是A. ，， B. ，， C. ，， D. ，，4.（3分）已知一组数据：，，，，，它们的平均数是，则的值为A.  B.  C.  D. 5.（3分）以下列三个数为边长的三角形能组成直角三角形的是 （  ）A. 1，1，2 B. 5，8，10
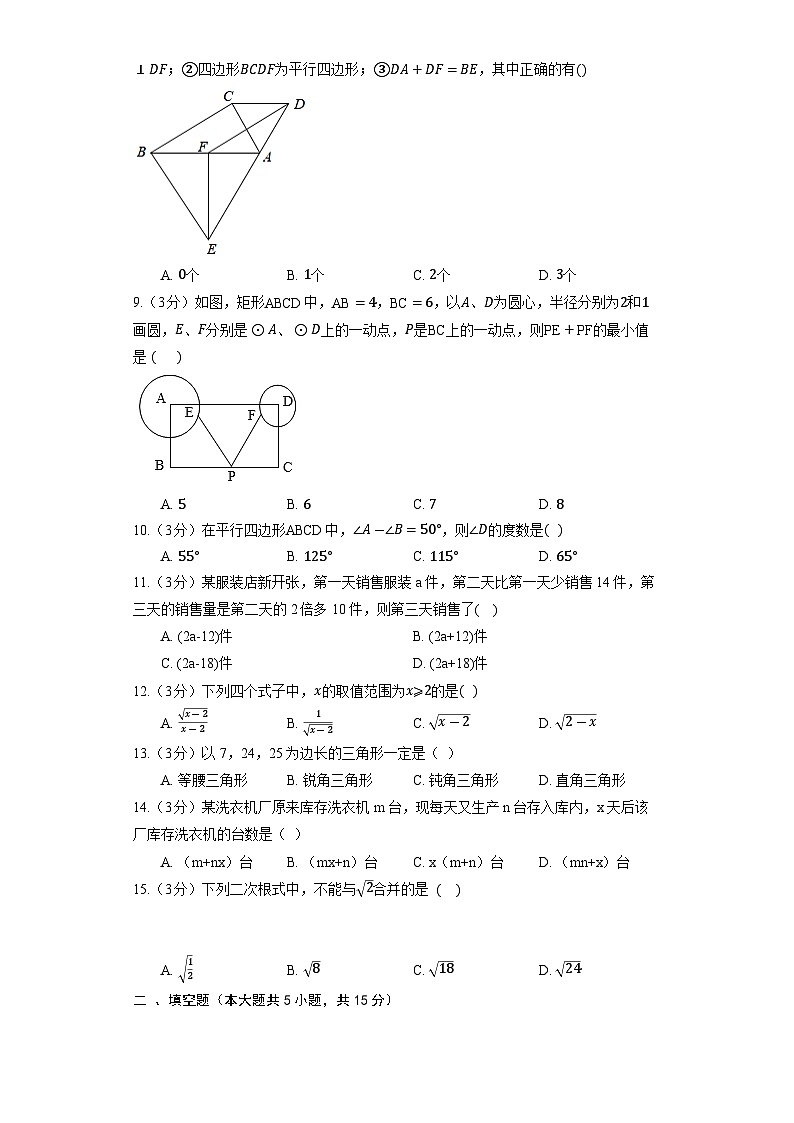
C. 6，7，8 D. 5，12，136.（3分）下列式子：，，，，，中，代数式的个数是A.  B.  C.  D. 7.（3分）如果，那么的取值范围是A.  B.  C.  D. 8.（3分）如图，分别以的直角边，斜边为边向外作等边和等边，为的中点，连接、，，则以下结论：①；②四边形为平行四边形；③，其中正确的有
 A. 个 B. 个 C. 个 D. 个9.（3分）如图，矩形中，，，以、为圆心，半径分别为和画圆，、分别是、上的一动点，是上的一动点，则的最小值是        
 A.        B.       C.        D. 10.（3分）在平行四边形中，，则的度数是A.  B.  C.  D. 11.（3分）某服装店新开张，第一天销售服装a件，第二天比第一天少销售14件，第三天的销售量是第二天的2倍多10件，则第三天销售了(    )A. (2a-12)件 B. (2a+12)件
C. (2a-18)件 D. (2a+18)件12.（3分）下列四个式子中，的取值范围为的是A.  B.  C.  D. 13.（3分）以7，24，25为边长的三角形一定是（  ）A. 等腰三角形 B. 锐角三角形 C. 钝角三角形 D. 直角三角形14.（3分）某洗衣机厂原来库存洗衣机m台，现每天又生产n台存入库内，x天后该厂库存洗衣机的台数是（  ）A. （m+nx）台 B. （mx+n）台 C. x（m+n）台 D. （mn+x）台15.（3分）下列二次根式中，不能与合并的是       
 A.  B.  C.  D. 二 、填空题（本大题共5小题，共15分）16.（3分）如图，，，，则阴影部分的面积是______.
 17.（3分）已知x2=196，|y|=5，且xy＜0，则x-2y的值为____．18.（3分）如图，在平行四边形中，对角线、交于点，是中点，若，则的长为 ______
 19.（3分）如图是一个数值转换机，若a输入的值为1，则输出的结果应为____．20.（3分）计算：______．三 、解答题（本大题共5小题，共40分）21.（8分）计算：22.（8分）如图，四边形是平行四边形，平分交于点，平分，交于点． 
求证：； 
连接，写出图中所有的全等三角形．不要求证明
 23.（8分）利用平移画一条直线和已知直线平行且两条平行线间的距离为，这样的直线可以画几条？
 24.（8分）某茶叶销售商计划将罐茶叶按甲、乙两种礼品盒包装出售，其中甲种礼品盒每盒装罐，每盒售价元；乙种礼品盒每盒装罐，每盒售价元，恰好全部装完．已知每罐茶叶的成本价为元，设甲种礼品盒的数量为盒，乙种礼品盒的数量为盒． 
当时． 
 ①求关于的函数关系式． 
②若罐茶叶全部售出后的总利润不低于元，则甲种礼品盒的数量至少要多少盒？ 
若罐茶叶全部售出后平均每罐的利润恰好为元，且甲、乙两种礼品盒的数量和不超过盒，求的最大值．25.（8分）实行垃圾分类是保护生态环境的有效措施．为了解社区居民掌握垃圾分类知识的情况，增强居民环保意识，某校环境保护兴趣小组从、两个小区各随机抽取位居民进行垃圾分类知识测试测试满分为分，现将测试成绩进行整理、描述和分析如下： 
小区位居民的测试成绩如下：，，，，，，，，，，，，，，，，，， 
小区位居民测试成绩的条形统计图如下： 
 
、小区抽取的居民测试成绩统计表如下：小区平均数中位数众数方差根据以上信息，回答下列问题： 
填空：______，______，______； 
请结合数据，分析本次测试中两个小区居民对垃圾分类知识的了解情况，并提出一条合理化建议．
答案和解析1.【答案】C;【解析】解：、，故此选项错误； 
、，故此选项错误； 
、，故此选项正确； 
、，故此选项错误． 
故选： 
直接利用幂的乘方运算法则以及单项式乘以单项式和二次根式的性质分别化简得出答案． 
此题主要考查了幂的乘方运算以及单项式乘以单项式和二次根式的性质等知识，正确掌握运算法则是解题关键．
 2.【答案】B;【解析】解：由图象可知，  
一次函数与轴交于点，随的增大而减小，  
故使成立的的取值范围为是，  
故选：． 
根据函数图象中的数据和一次函数的性质，可以得到使成立的的取值范围． 
该题考查一次函数的性质、一次函数的图象，解答本题的关键是明确题意，利用数形结合的思想解答．
 3.【答案】B;【解析】解：、， 
长为、、的三条线段不能围成三角形； 
B、，，， 
以、、为边长的三角形是直角三角形； 
C、，，， 
以、、为边长的三角形不是直角三角形； 
D、，，， 
以、、为边长的三角形不是直角三角形． 
故选：． 
由可排除选项，将两短边的平方相加，与最长边的平方进行比较，由此即可得出结论． 
该题考查了勾股定理的逆定理，牢记“如果三角形的三边长，，满足，那么这个三角形就是直角三角形”是解答该题的关键．
 4.【答案】B;【解析】解：由题意得： 
， 
解得： 
故选： 
根据算术平均数的计算公式列方程解答即可． 
此题主要考查了算术平均数的计算方法，掌握计算公式是解决问题的前提．
 5.【答案】D;【解析】A、12+12≠22，因此不是勾股数，故此选项错误； 
B、52+82≠102，因此不是勾股数，故此选项错误； 
C、62+72≠82，因此不是勾股数，故此选项错误； 
D、52+122=132，因此是勾股数，故此选项正确； 
故选：D．
 6.【答案】B;【解析】解：在，，，，，，中，代数式有，，，，，共有个； 
故选： 
代数式是指用、、、把数或表示数的字母连接起来的式子． 
此题主要考查了代数式，数与字母经过加减、乘除、乘方、开方运算是代数式．
 7.【答案】C;【解析】 
【分析】 
本题考查二次根式的性质与化简，属于基础题． 
根据二次根式的性质得到，解不等式即可． 
【解答】解：， 
， 
解得， 
故选C．
 8.【答案】C;【解析】解：，， 
，， 
是等边三角形， 
， 
， 
， 
为的中点， 
， 
， 
， 
四边形为平行四边形，故②正确； 
四边形为平行四边形， 
， 
又， 
，故①正确； 
和都是等边三角形， 
，，， 
， 
，故③错误； 
其中正确的有个， 
故选： 
由平行四边形的判定定理判断②正确，再由平行四边形的性质和平行线的性质判断①正确，然后由三角形三边关系判断③错误，即可得出结论． 
此题主要考查了平行四边形的判定和性质、含直角三角形的性质、等边三角形的性质、平行线的性质、三角形三边关系等知识；熟练掌握平行四边形的判定与性质和等边三角形的性质，证明四边形为平行四边形是解答该题的关键．
 9.【答案】C;【解析】 
该题考查了轴对称最短路线问题，勾股定理的应用等，作出对称图形是本题的关键． 
以为轴作矩形的对称图形以及对称圆，连接交于，交、于、，连接，交于，就是最小值；根据勾股定理求得的长，即可求得的最小值． 
 
解：如图，以为轴作矩形的对称图形以及对称，连接交于，交、于、，连接，交于， 
则就是的最小值； 
 
矩形中，，，和的半径为和， 
，，，， 
， 
， 
， 
故选C．
 10.【答案】D;【解析】解：在平行四边形中，，  
又有，  
把这两个式子相加即可求出，，  
故选：． 
利用平行四边形的邻角互补，和已知，就可建立方程求出未知角． 
该题考查了平行四边形的性质：邻角互补，对角相等，建立方程组求解．
 11.【答案】C;【解析】由题意可知：第三天的销售量是2(a-14)+10=(2a-18)件．故选C。
 12.【答案】C;【解析】解：、，且，解得：，故A错误；  
B、，解得：，故B错误；  
C、，解得，故C正确；  
D、，解得，故D错误；  
故选：． 
根据分式有意义的条件是分母不等于零，二次根式中的被开方数是非负数分别进行分析即可． 
此题主要考查了二次根式有意义的条件，以及分式有意义的条件，题目比较基础．
 13.【答案】D;【解析】解：∵72+242=252， 
∴这个三角形一定是直角三角形． 
故选：D．
 14.【答案】A;【解析】解：∵每天生产n台存入库内， 
∴x天后生产nx台存入库内， 
∵原来库存洗衣机m台， 
∴x天后该厂库存洗衣机的台数是（m+nx）台． 
故选A．
 15.【答案】D;【解析】【分析】本题考查了同类二次根式，根据二次根式的乘除法，可化简二次根式，根据最简二次根式的被开方数相同，可得答案．【解答】解：．，故A能与合并，该选项错误； 
B.，故B能与合并，该选项错误； 
C.，故C能与合并，该选项错误； 
D.，故D不能与合并，该选项正确．故选D．
 16.【答案】25.12;【解析】解：，，， 
， 
故阴影部分的面积是 
故答案为： 
根据勾股定理可求的长，再根据圆的面积公式，即可得到阴影部分的面积． 
考查了勾股定理和圆的面积计算，勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
 17.【答案】±24;【解析】解：∵=196，|y|=5，且xy＜0， 
∴x=14，y=-5；x=-14，y=5， 
则x-2y=±24． 
故答案为：±24．
 18.【答案】6;【解析】解：四边形是平行四边形， 
，， 
， 
， 
是的中位线， 
， 
 
故答案为： 
由平行四边形中，对角线和交于点，，可得是的中位线，根据三角形中位线的性质，即可求得的长． 
此题主要考查了平行四边形的性质以及三角形中位线的性质．此题比较简单，注意掌握数形结合思想的应用．
 19.【答案】7;【解析】解：a=1时，输出的值=（12-2）×（-3）+4， 
=（-1）×（-3）+4， 
=3+4， 
=7． 
故答案为：7．
 20.【答案】;【解析】解：原式， 
故答案为：． 
首先把与化简，再合并同类二次根式即可． 
此题主要考查了二次根式的加减，关键是正确把二次根式化简成最简二次根式．
 21.【答案】解：原式 ．;【解析】直接利用完全平方公式以及结合二次根式的性质化简进而得出答案．
 22.【答案】证明：（1）∵四边形ABCD是平行四边形， 
∴DC∥AB， 
∴∠CDE=∠AED， 
∵DE平分∠ADC， 
∴∠ADE=∠CDE， 
∴∠ADE=∠AED， 
∴AE=AD， 
同理可得CF=CB， 
又∵AD=CB， 
∴AE=CF， 
∵AB=CD， 
∴DF=BE， 
∴四边形DEBF是平行四边形， 
∴DE=BF， 
 
（2）△ADE≌△CBF，△DFE≌△BEF．;
 【解析】 
由平行四边形的性质和已知条件证明四边形是平行四边形，根据平行四边形的性质可得到； 
连接，则图中所有的全等三角形有：≌，≌． 
该题考查了平行四边形的性质、角平分线的特点、等腰三角形的判定和性质以及全等三角形的判定，题目难度不大．
 23.【答案】解：平移画一条直线和已知直线l平行且两条平行线间的距离为2cm，这样的直线可以画2条．;【解析】 
根据平移的性质和平行线的性质即可得到结论． 
此题主要考查了平移的性质，平行线的性质，熟练掌握平移的性质是解答该题的关键．
 24.【答案】解：①由题意，得， 
． 
②由题意，得，又， 
， 
解得， 
甲种礼品盒的数量至少要盒，此时乙种礼品盒的数量要盒，符合题意． 
由题意，得， 
， 
，，又，， 
因为是整数，所以的最大值为， 
的最大值为．;【解析】 
①根据题意列出函数解析式即可； 
②根据题意列出不等式，进而解答即可； 
根据条件求出，再根据题中条件求得的最大值． 
本题考查一次函数的应用、不等式的应用、一元一次方程等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
 25.【答案】7.3  7.5  8;【解析】解：小区位居民的测试成绩中分出现次数最多，有次， 
所以其众数， 
小区位居民的测试成绩的平均数， 
其中位数， 
故答案为：、、； 
比较、小区位居民的测试成绩知，两小区居民测试成绩的平均数、中位数均相等， 
而小区测试成绩的方差小于小区， 
所以小区测试成绩波动幅度小； 
建议：加强对小区保护生态环境意识答案不唯一 
根据平均数、众数和中位数的定义求解即可； 
根据平均数、中位数、方差的意义求解即可． 
此题主要考查条形统计图、众数与中位数的意义，中位数是将一组数据从小到大或从大到小重新排列后，最中间的那个数最中间两个数的平均数，叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会错误地将这组数据最中间的那个数当作中位数．