初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理课文配套课件ppt

这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理课文配套课件ppt，共16页。PPT课件主要包含了a2＋b2＝c2，如何证明呢，S＝a2＋b2，＝c2，刘徽证明，勾股定理的证明等内容，欢迎下载使用。
命题如果直角三角形两直角边长分别为 a，b，斜边长为 c，那么__________．
右图是我国古代证明该命题的“赵爽弦图”．
赵爽指出：按弦图，又可以勾股相乘为朱实二，倍之为朱实四．以勾股之差自相乘为中黄实．加差实，亦成弦实．
你是如何理解的？你会证明吗？
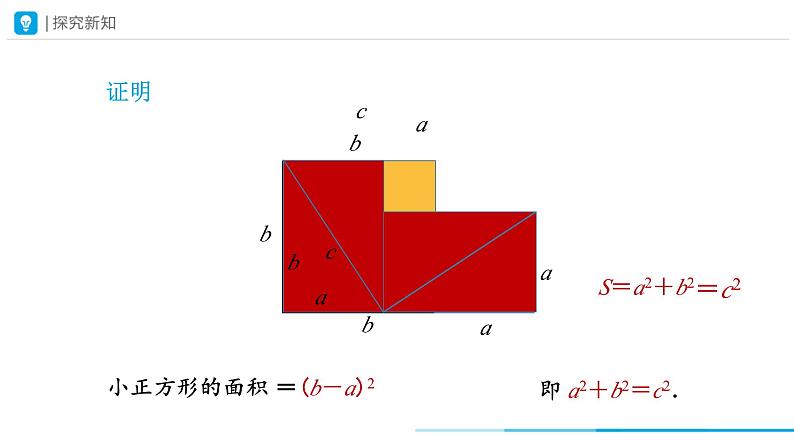
小正方形的面积 ＝(b－a)2
即 a2＋b2＝c2．
图形在经过适当分割后再另拼接成一个新的图形，分割拼接前后图形的各部分的面积之和不变．
你理解了吗？原命题是否正确？
原命题是正确的，又因为该命题与直角三角形的边有关，我国把它称为勾股定理．即：
如果直角三角形两直角边长分别为 a，b，斜边长为 c，那么 a2＋b2＝c2．
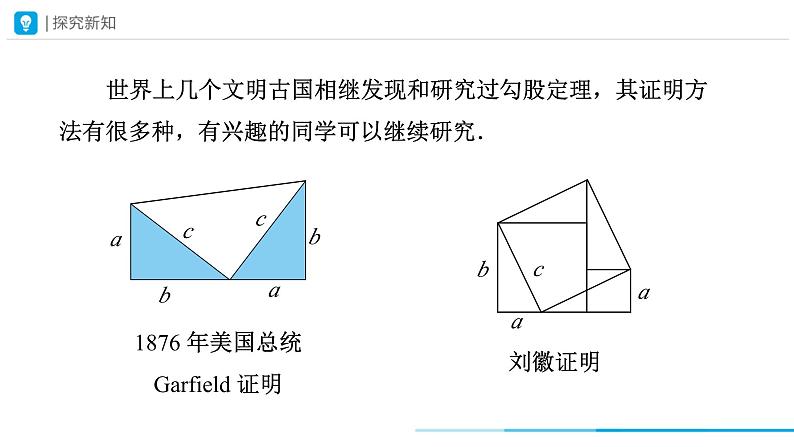
世界上几个文明古国相继发现和研究过勾股定理，其证明方法有很多种，有兴趣的同学可以继续研究．
1876 年美国总统 Garfield 证明
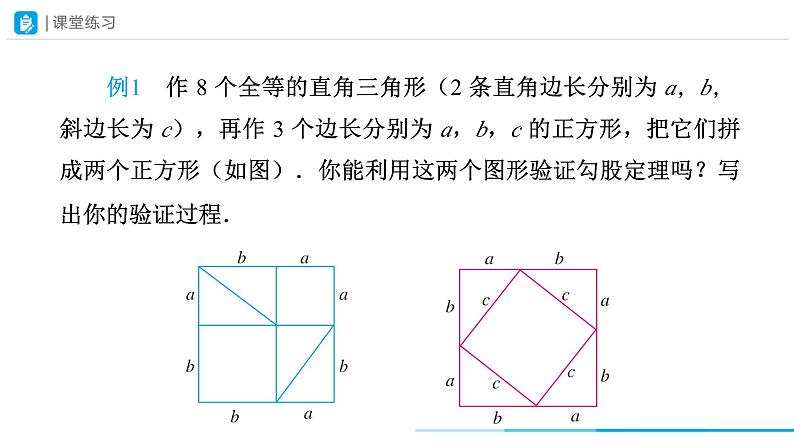
例1　作 8 个全等的直角三角形（2 条直角边长分别为 a，b， 斜边长为 c），再作 3 个边长分别为 a，b，c 的正方形，把它们拼成两个正方形（如图）．你能利用这两个图形验证勾股定理吗？写出你的验证过程．
解：由图可知大正方形的边长为：a＋b，则面积为(a＋b)2，由左图可得 (a＋b)2＝a2＋b2＋4× ，由右图可得 (a＋b)2＝c2＋4× ．根据面积相等，所以 a2＋b2＝c2．
用分割拼接法证明勾股定理，其依据是“分割拼接前后图形的各部分的面积之和不变”．
例2　某同学提出了一种证明勾股定理的方法：如图 1，点 B 是正方形 ACDE 的边 CD 上一点，连接 AB，得到 Rt△ACB，三边分别为 a，b，c，将 △ACB 裁剪拼接至 △AEF 位置，如图 2，该同学用图 1、图 2 的面积不变证明了勾股定理．请你写出该方法证明勾股定理的过程．
根据两图形面积相等，所以 c2＋ (b2－a2) ＝ b2．化简，得 a2＋b2＝c2．
熟练掌握勾股定理的证明方法，一般先利用拼图，再利用面积相等．本题在利用面积相等时，关键是作辅助线，然后用含字母 c 的表达式来表示图 2 的面积．
证明勾股定理的一般方法
“赵爽弦图”法证明勾股定理