人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.2 命题、定理、证明完美版课件ppt

这是一份人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.2 命题、定理、证明完美版课件ppt，共23页。PPT课件主要包含了3平行线的性质，对顶角的性质，平行线的判定方法，平行公理的推论，平行线的性质，如果那么，已知事项推出的事项，两直线平行，内错角相等，1同位角相等等内容，欢迎下载使用。

第五章 相交线与平行线
5.3.2 命题、定理、证明
比比谁能答得又快又准.
请记录并观察，请说出这些语句的共同特征？
1. 对顶角相等；2. 如果两条直线都与第三条直线平行，那么这两条直线也相互平行；3. 同位角相等，两直线平行； 4. 两条平行线被第三条直线所截，同旁内角互补.
都是在对一件事进行判断.
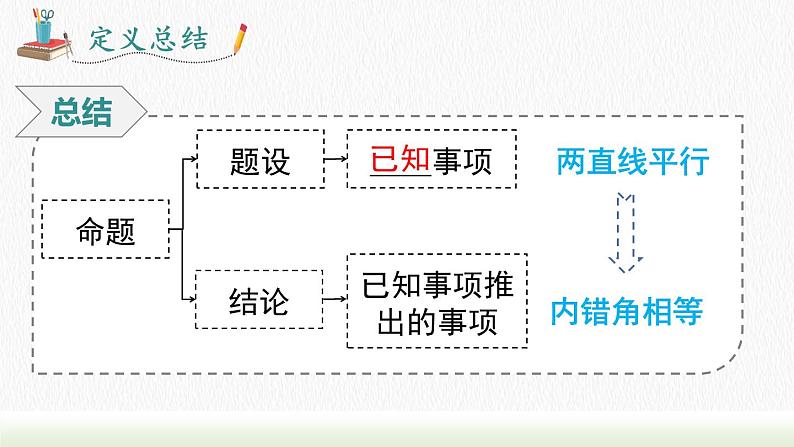
知识点1：命题的定义与结构
像这样判断一件事的语句，叫做命题.
例如： 1. 相等的角是对顶角. 2. 画线段 AB = CD.
例1 判断下列四个语句中，哪个是命题，哪个不是命题，并说明理由：
(1) 对顶角相等吗？
(2) 画一条线段 AB = 2 cm；
(3) 两直线平行，同位角相等；
(4) 相等的两个角，一定是对顶角.
思路点拨：是否判断一件事.
观察下列命题，你能发现这些命题有什么共同的结构特征？与同伴交流.(1) 如果两个三角形的三条边分别相等，那么这两个三角形的周长相等；(2) 如果两个数的绝对值相等，那么这两个数也相等；(3) 如果一个数的平方等于 9，那么这个数是 3.
例2 请将命题“对顶角相等”改写成“如果那么”形式.
思路点拨：有些命题题设和结论不明显，需要进行分析找出，改写前后命题意义不发生改变.
如果两个角是对顶角，那么这两个角相等.
1.请将下列命题改写成“如果那么”形式，并指出题设和结论.
(2) 垂直于同一直线的两条直线互相垂直.
(3) 过一点有且只有一条直线与已知直线平行.
如果两个角是同位角，那么这两个角相等.
如果两条直线垂直于同一直线，那么这两条直线互相垂直.
如果过一点向已知直线做平行线，那么这种直线有且只有一条.
知识点2：真命题与假命题
命题 1：如果一个数能被 4 整除，那么它也能被 2 整除.
观察下列命题，你能发现它们有什么不同的特点吗？
命题 2：如果两个角互补，那么它们是邻补角.
如果题设成立，那么结论一定成立，这样的命题叫做真命题.如果题设成立，不能保证结论一定成立，这样的命题叫做假命题.
(1) 同旁内角互补 ( )
(4) 两点可以确定一条直线 ( )
(7) 互为邻补角的两个角的平分线互相垂直( )
(2) 一个角的补角大于这个角 ( )
2. 判断下列命题的真假.
(5) 两点之间线段最短 ( )
(3) 相等的两个角是对顶角 ( )
(6) 同角的余角相等 ( )
线段公理：两点之间线段最短.
补角的性质、余角的性质等.
例3 已知：b∥c，a⊥b．
∠2 = ∠1 = 90°
证明：∵ a⊥b(已知)， ∴ ∠1 = 90°(垂直的定义).又 ∵ b∥c(已知)，∴∠2 =∠1 = 90°(两直线平行，同位角相等). ∴ a⊥c(垂直的定义).
3. 已知三条不同的直线 a，b，c，在同一平面内，下列四个命题： ①如果 a∥b，a⊥c，那么 b⊥c； ②如果 b∥a， c∥a，那么 b∥c； ③如果 b⊥a，c⊥a，那么b⊥c； ④ 如果 b⊥a，c⊥a，那么 b∥c，其中真命题的有______（填序号）.
1. 下列关于命题的描述中，正确的是 ( )
A. 命题一定是正确的 B. 真命题一定是定理C. 定理一定是真命题D. 一个反例不足以说明一个命题为假命题
2. 命题“内错角相等”是真命题吗？若是，说出理由，若不是，请举出反例.
答：不是真命题.必须是两直线平行，内错角相等.　　反例：两条相交的直线都和第三条直线相交，内错角不相等.
判断假命题，只需举一个例子(反例)，它符合命题的题设，但不满足结论就可以.
3. 如图，现有以下 3 个论断：①AB//BC；②∠B = ∠C；③∠E = ∠F.请以其中的两个论断为条件，另一个论断为结论构造命题. (1) 你构造的是哪几个命题？ (2) 请选择其中的一个真命题加以证明.
例：若 AB//CD，∠B=∠C，则∠E=∠F.
解：(2)例：若 AB//CD，∠B = ∠C，则∠E = ∠F. 证明： 如图，∵AB//CD， ∴∠B = ∠CDF. ∴CE//BF. ∴∠E = ∠F.