第5章 生活中的轴对称-小结与复习 北师版数学七年级下册课件

这是一份第5章 生活中的轴对称-小结与复习 北师版数学七年级下册课件，共32页。

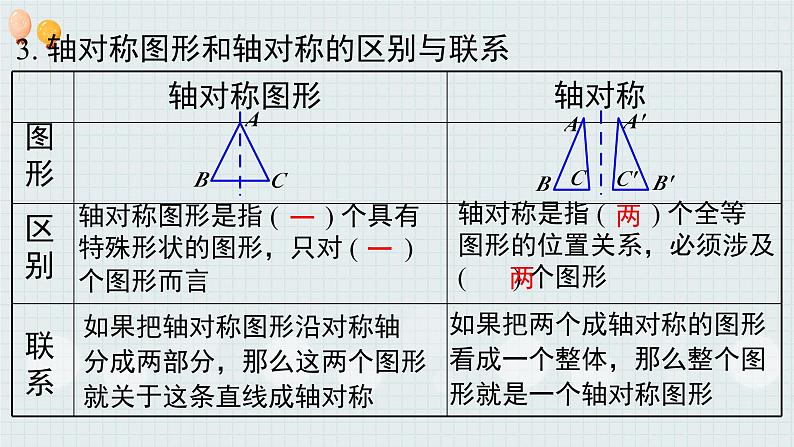
小结与复习第五章 生活中的轴对称1. 轴对称图形：如果一个平面图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形就叫做轴对称图形，这条直线叫做对称轴.2. 轴对称：如果两个平面图形沿一条直线对折后能够完全重合，那么称这两个图形成轴对称，这条直线叫做这两个图形的对称轴.一. 轴对称图形与轴对称1. 成轴对称的两个图形沿对称轴折叠能够完全重合， 轴对称图形是指单一图形，成轴对称是指两个图形.知识回顾3. 轴对称图形和轴对称的区别与联系 轴对称图形轴对称 区别联系图形 轴对称图形是指 ( ) 个具有特殊形状的图形，只对 ( ) 个图形而言轴对称是指 ( ) 个全等图形的位置关系，必须涉及 ( ) 个图形如果把轴对称图形沿对称轴 分成两部分，那么这两个图形 就关于这条直线成轴对称如果把两个成轴对称的图形 看成一个整体，那么整个图形就是一个轴对称图形一一两两4. 轴对称的性质： 在轴对称图形或两个成轴对称的图形中，对应点所连的线段被对称轴垂直平分，对应线段相等，对应角相等.1. 等腰三角形的性质 二. 简单的轴对称图形2. 等腰三角形的性质① 等腰三角形的两个底角相等.② 等腰三角形“三线合一”.知识回顾等边三角形三条边相等，三个角相等且都为60°.角平分线上的点到这个角的两边的距离相等.3. 角平分线的性质2. 线段垂直平分线的性质 线段垂直平分线上的点到线段两个端点的距离相等. 例1 对称现象无处不在，请你观察下面的四个图形，其中，可以看作是轴对称图形的有（ ） A.1个 B.2个 C.3个 D.4个D例2：小华在镜中看到身后墙上的钟，钟面上指针显示的时刻为8:45，那么此时的实际时间是多少？解：此时的实际时间是3:15. 例3 如图，是由三个小正方形组成的图形，请你在图中补画一个小正方形，使补画后的图形为轴对称图形．最多有几种？ 例4 如图，△ABC的三边AB，BC，CA的长分别是20,30,40，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于（ ）．A.1:1:1B.1:2:3C.2:3:4D.3:4:5CBAOC1.在轴对称图形中，对应点所连线段被________垂直平分.2.如图，△ABC中，∠A=30°，∠C = 90°，BD平分∠ABC，若AD = 6cm，则AC= ___cm.对称轴9随堂演练3.判断① 等腰三角形、角和圆都是轴对称图形.×√② 所有的直径都是圆的对称轴.③ 在轴对称图形中，对应线段的延长线不一定交在对称轴上.④ 等腰三角形只有一条对称轴.××4.画出下列是轴对称图形的所有对称轴.5.如图，∠A=60°，CE⊥AB于E，BD⊥AC于D，BD与CE相交于点H，HD=1，HE=2，试求BD和CE的长.（直角三角形30度角所对的边等于斜边的一半）解：∵∠A = 60°， CE⊥AB，BD⊥AC， ∴∠ACE = 30°， ∠ABD = 30°. ∵HE = 2， ∴BH = 2HE = 4.∵HD = 1，∴HC = 2HD = 2.∴BD = BH + HD = 5，CE = CH + HE = 4.6.如图，点P是∠AOB内一点，∠AOB=30°，OP=10，点M、N分别是OA、OB上的动点，试通过作图说明△PMN周长的最小值是多少？解：如图，分别作P点关于OA、OB的对称点P1，P2，连接P1P2与OA相交于点M，与OB相交于点N，则此时△PMN的周长最小（三点共线）.连接 OP1，OP2，则∠P1OP2 = 2∠AOB = 60°，OP1 = OP = OP2，∴△OP1P2 是等边三角形，∴P1P2=OP1=OP=10，∴PM+MN+NP=P1M+MN+NP2=P1P2=10.即△PMN 周长的最小值为10.例1 如图，△ABC 和△A′B′C′ 关于直线 MN 对称，△A″B″C″ 和△A′B′C′ 关于直线 EF 对称.(1) 画直线 EF；(2) 直线 MN 与 EF 相交于点 O，试探究∠BOB″ 与直线 MN，EF 所夹锐角 α 的数量关系.【分析】连接△A′B′C′ 和△A″B″C″中的任意一对对应点，作所得线段的垂直平分线即为直线 EF，根据轴对称的性质可求角的数量关系.ABCA′B′C′A″B″C″解：（1）如图，连接 B′B″，作线段 B′B″ 的垂直平分线EF，则直线 EF 是△A′B′C′ 和△A″B″C″ 的对称轴；（2）连接 B″O，B′O，BO.因为 △ABC 和△A′B′C′ 关于直线 MN 对称，所以∠BOM =∠B′OM.因为△A″B″C″ 和△A′B′C′ 关于直线 EF 对称，所以∠B′OE =∠B″OE.所以∠BOB″ = 2(∠B′OM +∠B′OE) = 2α.MN 1. 下面的图形是轴对称图形吗? 如果是，你能指出它的对称轴吗?2. 如图所示，作出△ABC 关于直线 l 的对称图形．解：△A′B′C′ 就是所求作的图形.l例2 如图所示，在△ABC 中，AB = AC，BD⊥AC 于 D.试说明：∠BAC = 2∠DBC.【分析】根据等腰三角形“三线合一”的性质，可作顶角∠BAC 的平分线，来获取角之间的数量关系.解：作∠BAC 的平分线 AE，交 BC 于点 E，如图. 所以 AE⊥BC，所以∠AEC = 90°，∠2 +∠ACB = 90°. 因为 BD⊥AC，所以∠BDC = 90°，∠DBC +∠ACB = 90°.所以∠2 =∠DBC.所以∠BAC = 2∠DBC.因为 AB = AC，例3 如图，在△ABC 中，AB＝AC＝20 cm，DE 垂直平分 AB，垂足为 E，交 AC 于 D，若△DBC 的周长为 35 cm，则 BC 的长为 (　　)A．5 cm B．10 cm C．15 cm D．17.5 cmC解析：因为 DE 垂直平分 AB，所以 AD＝BD. 所以△DBC 的周长为 BC＋BD＋CD＝BC＋AD＋CD＝BC＋AC＝35 cm. 因为 AC＝20 cm，所以 BC＝35－20＝15 (cm). 常常运用线段的垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”进行线段之间的转化，从而来求线段之间的关系及和差等，有时候与等腰三角形的“三线合一”结合起来考查.例4 有公路 l1 同侧、l2 异侧的两个城镇 A，B，如图. 电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇 A，B 的距离必须相等，到两条公路 l1，l2 的距离也必须相等，发射塔 C 应修建在什么位置？请用尺规作图找出所有符合条件的点，注明点 C 的位置 (保留作图痕迹，不要求写出画法).【解析】利用线段垂直平分线及角平分线的性质解题.解：根据题意知道，点 C 应满足两个条件：一是在线段 AB 的垂直平分线上；二是在两条公路夹角的平分线上，所以点 C 应是它们的交点.(2) 作线段 AB 的垂直平分线 FG；则射线 OD，OE 与直线 FG 的交点 C1，C2 就是所求的位置.(1) 作两条公路夹角的平分线 OD 和 OE；3. 如图，在△ABC 中，DE 是 AC 的垂直平分线，AC = 5 厘米，△ABD 的周长等于 13 厘米，则△ABC 的周长是 厘米.18生活中的轴对称轴对称现象两个图形成轴对称，及其对称轴轴对称图形，及其对称轴简单的轴对称图形等腰三角形的性质轴对称的性质对称性“三线合一”底角相等线段垂直平分线上的点到这条线段两个端点的距离相等角平分线上的点到这个角的两边的距离相等应用图案设计计算与推理