2023年陕西省宝鸡市渭滨区九年级中考二模数学试题

九年级·数学（二）试题

注意事项：

1.本试卷分为第一部分（选择题）和第二部分（非选择题）。全卷共6页，总分120分。考试时间120分钟。

2.领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号。

3.请在答题卡上各题的指定区域内作答，否则作答无效。

4.考试结束，本试卷和答题卡一并交回。

第一部分（选择题 共24分）

一、选择题（共8小题，每小题3分，计24分。每小题只有一个选项是符合题意的）

1.的绝对值是（    ）

A. B. C. D.

2.如图，直线，等腰直角三角形的直角顶点在上，若，则图中与互余的角的个数是（    ）

A.8 B.7 C.6 D.5

3.计算：（    ）

A. B. C. D.

4.如图，中，，，边上中线交于点，则的面积为（    ）

A.6 B.4 C.5 D.7

5.两条直线，关于轴对称，经过点，经过点，则这两条直线，的交点坐标为（    ）

A. B. C. D.

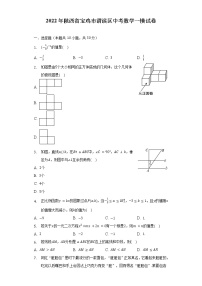
6.如图，点是矩形的中心，，，过点作两条互相垂直的直线，分别交、于点、点，交、于点、点，当时，长为（    ）

A. B. C.3 D.

7.如图，内接于，，的平分线交于点，连接，当点平分时，的度数为（    ）

A. B. C. D.

8.已知两点，均在抛物线上，点是该抛物线的顶点。若，则的取值范围是（    ）

A. B. C. D.

第二部分（非选择题 共96分）

二、填空题（共5小题，每题3分，计15分）

9.在下列各数，，，0.12112中，无理数的个数是________.

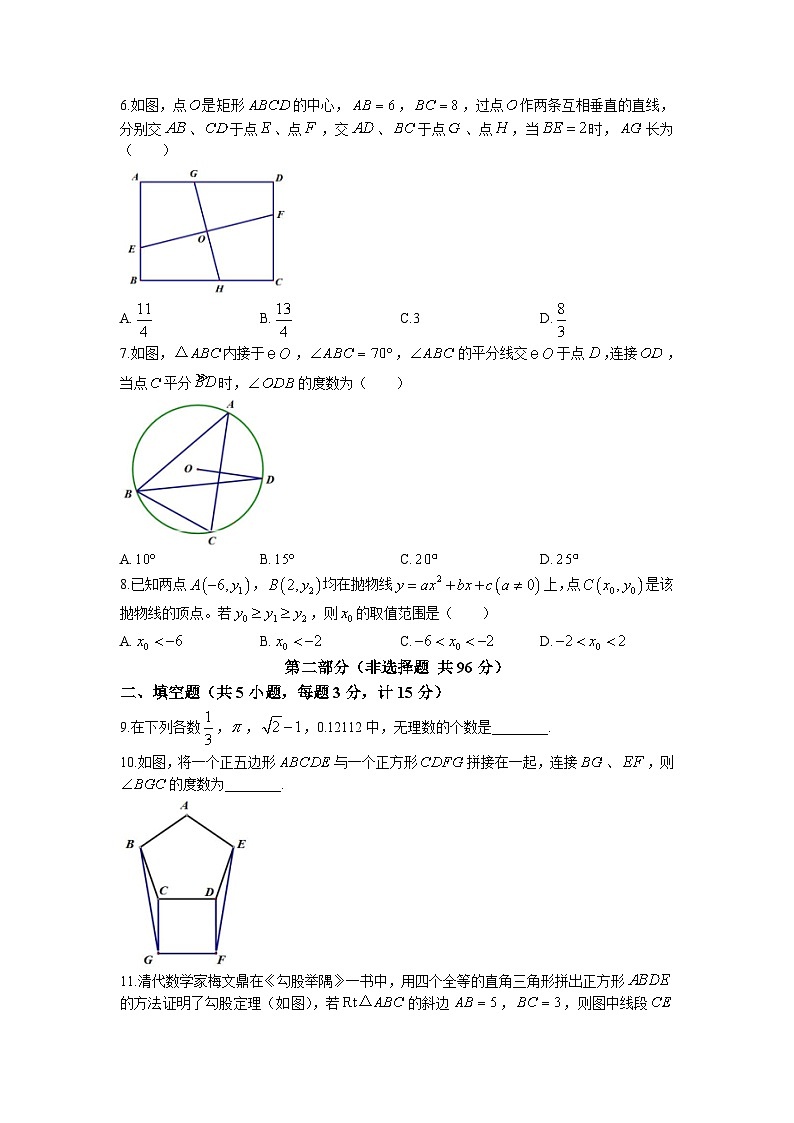
10.如图，将一个正五边形与一个正方形拼接在一起，连接、，则的度数为________.

11.清代数学家梅文鼎在《勾股举隅》一书中，用四个全等的直角三角形拼出正方形的方法证明了勾股定理（如图），若的斜边，，则图中线段的长为________.

12.已知点在反比例函数的图象上，若点关于轴对称的点在反比例函数的图像上，则的值为________.

13.如图，平行四边形中，对角线、交于点，，，、分别为、上两点，且，连接、，则与的面积比为________.

三、解答题（共13小题，计81分，解答应写出过程）

14.（本题满分5分）计算：.

15.（本题满分5分）解不等式，并写出它的正整数解.

16.（本题满分5分）化简：.

17.（本题满分5分）已知，如图所示，，请用尺规作图法求作边上的高.（保留作图痕迹，不写作法）

18.（本题满分5分）如图，点、均在线段上，且，分别过、作，，连接、，连接交于点，若，求证：.

19.（本题满分5分）如图，的顶点坐标为，，.

（1）画出向右平移3个单位后的；

（2）将绕原点旋转，画出旋转后的；

（3）的面积为________.

20.（本题满分5分）“诵读经典，传承文明”，为了弘扬中华传统文化，某校近期举办了“国学经典诵读大赛”，诵读的篇目分成四种类型：.蒙学今诵；.爱国传承；.励志劝勉；.秀山丽水，每种类型的篇目数相同，参赛者需从这四种类型中随机抽取一种诵读类型。

（1）小颖参加了这次大赛，她从中随机抽取一个类型，恰好抽中“.爱国传承”的概率是________；

（2）小红和小明也参加了这次大赛，请用树状图或列表法求他们抽中同一种类型篇目的概率.

21.（本题满分6分）如图，某海域有两个海拔均为150米的海岛和海岛，一勘测飞机在距离海平面垂直高度为1050米的空中飞行，飞行到点处时测得正前方一海岛顶端的俯角是，然后沿平行于的方向水平飞行20千米到达点处，在处测得正前方另一海岛顶端的俯角是，求两海岛间的距离.

22.（本题满分7分）运算能力是数学能力的重要组成部分。为提高学生运算能力，我校八年级开展了“打卡二十一天，运算大比拼”的竞赛活动。现从八年级（1）、（2）两个班（各班均为60人）各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：

收集数据：

1班：79，85，73，80，75，76，87，70，75，94，

75，79，81，71，75，80，86，59，83，77.

2班：92，74，87，82，72，81，94，83，77，83，

80，81，71，81，72，77，82，80，70，41.

整理数据：

分析数据：

应用数据：

（1）由上表填空：________，________，________，________.

（2）估计两个班级学生在本次比拼中成绩在90分以上（含90分）的共有多少人？

（3）你认为哪个班级的学生运算能力的总体水平较好，请说明理由.

23.（本题满分7分）如图1，某商场在一楼到二楼之间没有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行，甲乘自动扶梯，乙走步行楼梯，甲离一楼地面的高度（单位：）与下行时间（单位：）之间具有函数关系，乙离一楼地面的高度（单位：）与下行时间（单位：）的函数关系如图2所示.

（1）求关于的函数表达式；

（2）请通过计算说明甲、乙两人谁先到达一楼地面。

24.（本题满分8分）如图，为的弦，交于点，交过点的直线于点，且.

（1）试判断直线与的位置关系，并说明理由；

（2）若，，求的长.

25.（本题满分8分）某公园在垂直于湖面的立柱上安装了一个多孔喷头，从喷头每个孔喷出来的水柱形状都相同，可以看作是抛物线的一部分，当喷头向四周同时喷水时，形成一个环状喷泉.安装后，通过测量其中一条水柱，获得如下数据，在距立柱水平距离为米的地点，水柱距离湖面的高度为米.

（1）在如下网格中建立适当的平面直角坐标系，根据已知数据描点后用平滑的曲线连接，并求所画图象对应的函数表达式；

（2）从安全的角度考虑，需要在这个喷泉外围设立一圈正方形护栏，这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米，请通过计算说明公园至少需要准备多少米的护栏？（不考虑接头等其他因素）

26.（本题满分10分）

问题情境：（1）数学活动课上，王老师提出一个问题：如图1，四边形是正方形，是上的任意一点，于点，交于点，则线段、、之间的数量关系是________.

建立模型：（2）某数学小组小明同学受此启发，提出了如下问题：如图2，四边形是正方形，，是对角线上的点，，连接，.求证：四边形是菱形.

模型拓展：（3）该数学小组的同学们在王老师的指导下大胆尝试，改变图形模型，发现并提出新的探究点：如图3，若正方形的边长为12，是对角线上的一点，过点作，交边于点，连接，交对角线于点，.求的值.

九年级·数学（二）试题答案

一、选择题（共8小题，每小题3分，计24分。每小题只有一个选项是符合题意的）

二、填空题（共5小题，每题3分，计15分）

9.2 10. 11. 12.              13.

三、解答题（共13小题，计81分，解答应写出过程）

14.（本题满分5分）

解：原式

15.（本题满分5分）

解：

∴原不等式的正整数解为1，2，3.

16.（本题满分5分）

解：原式

17.（本题满分5分）

解：过点做直线的垂线，垂足为，则线段即为所求.（作图略）

18.（本题满分5分）

证明：连接、，

∵，，

∴，.

在和中，

∴

∴

∴四边形为平行四边形，

∴

19.（本题满分5分）

（1）（2）略；（3）5

20.（本题满分5分）

解：（1）；

（2）

如上表，共有16种等可能的情况，其中小红和小明抽中同一种类型篇目的结果有4种，故（小红和小明抽中同一种类型篇目）.

21.（本题满分6分）

解：如图，过点作于点，过点作，交延长线于点，则四边形为矩形，所以，，

由题意可知（米），（米），

∴在中，，（米），

∴（米）

在中，，（米），

∴（米），

∴两海岛间的距离是米.

22.（本题满分7分）

解：（1）11，10，78，81.

（2）两个班级学生在本次比拼中成绩在90分以上的共有（人）。

（3）两个班平均分相同，但是（2）班的中位数较高，得高分人数相对较多，因此（2）班的总体水平较好。

23.（本题满分7分）

解：（1）设关于的函数解析式是，

，解得，，

即关于的函数解析式是；

（2）当时，，得，

当时，，得，

∵，∴甲先到达地面.

24.（本题满分8分）

解：（1）直线与相切，理由：如图，连接，

∵，∴，

∵，∴，

∵，

∴，

∵，∴，∴，

∴，

∵为半径，∴直线与相切；

（2）在中，，

∵，

∴设，则，

∵，

∴，解得：或（不符合题意，舍去），

∴，

∵，

∴，

∵，，

∴，解得：，∴的长为6.

25.（本题满分8分）

解：（1）如图，

由和可知，抛物线的对称轴为，当时，，∴水柱最高点距离湖面的高度是5米，设二次函数的关系式为，把代入可得，

∴；

经过验证，，均满足上式。

（2）当时，即，

解得（舍去）或，

∴正方形的周长为（米），

∴至少需要准备栏杆（米），

∴公园至少需要准备72米的护栏.

26.（本题满分10分）

（1）

（2）证明：如图，连接，∵四边形是正方形，

∴，，.

∴.

∵，

∴.∴.

∴.∵，∴四边形是平行四边形.

∵，

∴四边形是菱形.

（3）解：如图，把绕点逆时针旋转后得到，连接，

∵四边形是正方形，

∴，.

∵，

∴，且，以为直径作圆，则点、、、均在此圆上.

∴，

∴.

由旋转的性质得：，

∴，，.

∵，∴.

∴，即.

∵

∴.∴.

∵，，∴.

由，设，则，

在中，，则，

∵正方形的边长为12，∴由勾股定理得：，即，解得.∴，.

∵，，∴.

∴，∴.