（课后作业设计）5.4三角形及多边形的内角和-2022-2023学年四年级数学下册课后作业设计（原卷版+解析版）人教版

2022-2023学年四年级数学下册课后作业设计之

5.4三角形及多边形的内角和（解析版）

    年    月    日      完成时间：    分    秒

一、填空题。

1．在一个三角形中，这个三角形是(        )。

【答案】直角三角形

【分析】三角形的两个内角的度数已知，于是可以求出这两个角的度数之和，依据三角形的内角和是180°，即可求出第三个内角的度数，从而可以判定这个三角形的类别。

【详解】180°－（38°＋52°）

＝180°－90°

＝90°

90°的角是直角，这个三角形是直角三角形。

【点睛】解答此题的主要依据是：三角形的内角和以及三角形的分类方法。

2．一个等腰三角形的顶角是50°，它的另一个底角是(        )°。

【答案】65

【分析】等腰三角形的两腰相等，两个底角也相等，三角形的内角和为180°，因此用180°减去顶角的度数后，再除以2，即可得到它的另一个底角的度数，依此计算。

【详解】180°－50°＝130°

130°÷2＝65°

即它的另一个底角是65°。

【点睛】熟记三角形的内角和度数以及等腰三角形的特点，是解答此题的关键。

3．一个直角三角形的一个角是80度，那另外两个角分别是(        )度和(        )度。

【答案】     90     10

【分析】三角形的内角和为180°，直角三角形中有一个角是90°，因此用180°减去90°后，再减去80°，即可得到第三个角的度数，依此解答。

【详解】180°－90°＝90°

90°－80°＝10°

即另外两个角分别是90度和10度。

【点睛】熟记三角形的内角和度数，以及直角三角形的特点，是解答此题的关键。

4．计算出下列三角形的∠1是多少度。

∠1＝(         )                         ∠1＝(         )

【答案】     60°##60度     121°##121度

【分析】三角形的内角和为180°。等边三角形的三条边相等，三个角相等，用三角形的内角和除以3，即可算出等边三角形的每个内角是多少度；用三角形的内角和减去钝角三角形的另外两个内角，即可算出钝角三角形的钝角是多少度。据此解答。

【详解】180°÷3＝60°

180°－23°－36°

＝157°－36°

＝121°

等边三角形的∠1＝60°，钝角三角形的∠1＝121°。

【点睛】本题主要考查学生对三角形内角和的掌握和对等边三角形特性的认识。牢记三角形内角和是解决此题的关键。

二、选择题。

5．下面平面图形中（         ）能单独密铺。

A．平行四边形 B．三角形 C．正五边形 D．正六边形

【答案】C

【分析】在拼接时，同一顶点处多个多边形的内角和是360°的可以密铺。

【详解】A．平行四边形的内角和是360°，用4个相同的平行四边形拼接时，每个角只需用一次，拼接点的四个角刚好能拼成一个周角，所以平行四边形能单独密铺。

B．三角形的内角和是180°，2个180°是360°，用6个相同的三角形拼接时，每个角只需用两次就能拼出一个周角，所以三角形能单独密铺。

C．正五边形的每个内角是108°，360°不是108°的整数倍，所以正五边形不能单独密铺。

D．正六边形的每个内角是120°，3个120°是360°，所以正六边形能单独密铺。

故答案为：

【点睛】所有任意三角形与任意四边形都可以单独密铺。

6．一块三角形玻璃破碎后的形状如下图，这个三角形是（         ）。

A．钝角三角形 B．直角三角形 C．锐角三角形 D．以上都有可能

【答案】A

【分析】因为三角形的内角度数和是180°，根据图中的两个内角度数可求打碎的一个角的度数，再根据三角形的分类即可作出判断。

【详解】180°－30°－40°

＝150°－40°

＝110°

故是一个钝角三角形。

故答案为：A

【点睛】考查了三角形的内角和定理：三角形的内角和等于180°；同时考查了三角形的按角分类，关键明确：①有一个角是直角的三角形是直角三角形，②三个角都为锐角的三角形是锐角三角形，③有一个角是钝角的三角形是钝角三角形。

7．一个三角形最小的内角是60°，这个三角形一定是（         ）三角形。

A．等边 B．等腰 C．钝角 D．直角

【答案】A

【分析】已知一个三角形最小的内角是60°，假设这个三角形另外一个内角也是60°，根据三角形的内角和是180°，计算出第三个内角的度数，再根据三角形的分类判断这个三角形的类型。

【详解】假设另一个内角也是60°，则第三个内角是：

180°－60°－60°＝60°

三角形的三个内角都是60°，所以这个三角形一定是锐角三角形或等边三角形。

故答案为：A

【点睛】本题考查三角形的内角和以及三角形的分类。

8．下图是一个四边形，∠1＋∠2＋∠3＋∠4等于（         ）。

A．180° B．540° C．360° D．720°

【答案】C

【分析】把该四边形作出对角线，可将四边形分成2个三角形，所以该四边形的内角和等于三角形内角和的2倍，而三角形内角和为180°，据此解答。

【详解】根据分析，∠1＋∠2＋∠3＋∠4＝180°×2＝360°

故答案为：C

【点睛】本题考查多边形的内角和，可把多边形分为若干个三角形，结合三角形内角和为180°进行计算。

三、图形计算。

9．求出图中未知角的度数。

（1）   （2）

【答案】（1）

（2）

【分析】（1）如图一个直角三角形，那么一个角是90度，另两个角的和是90度，用90度减去给出的一个角的度数就是所求的角的度数；

（2）根据三角形内角和度数是180度，减去所给的两个角的度数，就是所求角的度数，据此解答。

【详解】（1）

（2）

10．求出各题中∠1的度数。

【答案】57°；63°

【分析】（1）观察图形可知，三角形的第三个内角与115°组成平角，平角＝180°，据此利用180°减去115°，先求出三角形的第三个内角的度数；再根据三角形的内角和是180°，用180°减去两个已知角的度数就等于∠1的度数；

（2）根据四边形的内角和是360°，用360°减去三个已知角的度数就等于∠1的度数。

【详解】180°－58°－（180°－115°）

＝180°－58°－65°

＝122°－65°

＝57°

360°－117°－63°－117°

＝243°－63°－117°

＝180°－117°

＝63°

1．一个直角三角形中，一个锐角角是70度，那么另一个锐角是多少度？

【答案】20度

【分析】根据在直角三角形中，另两个锐角和为90°，已知一个锐角，用减法即可求得另一个锐角的度数，据此解答。

【详解】

答：另一个锐角是20度。

【点睛】本题考查了直角三角形的性质，是基础题，应注意基础知识的积累。

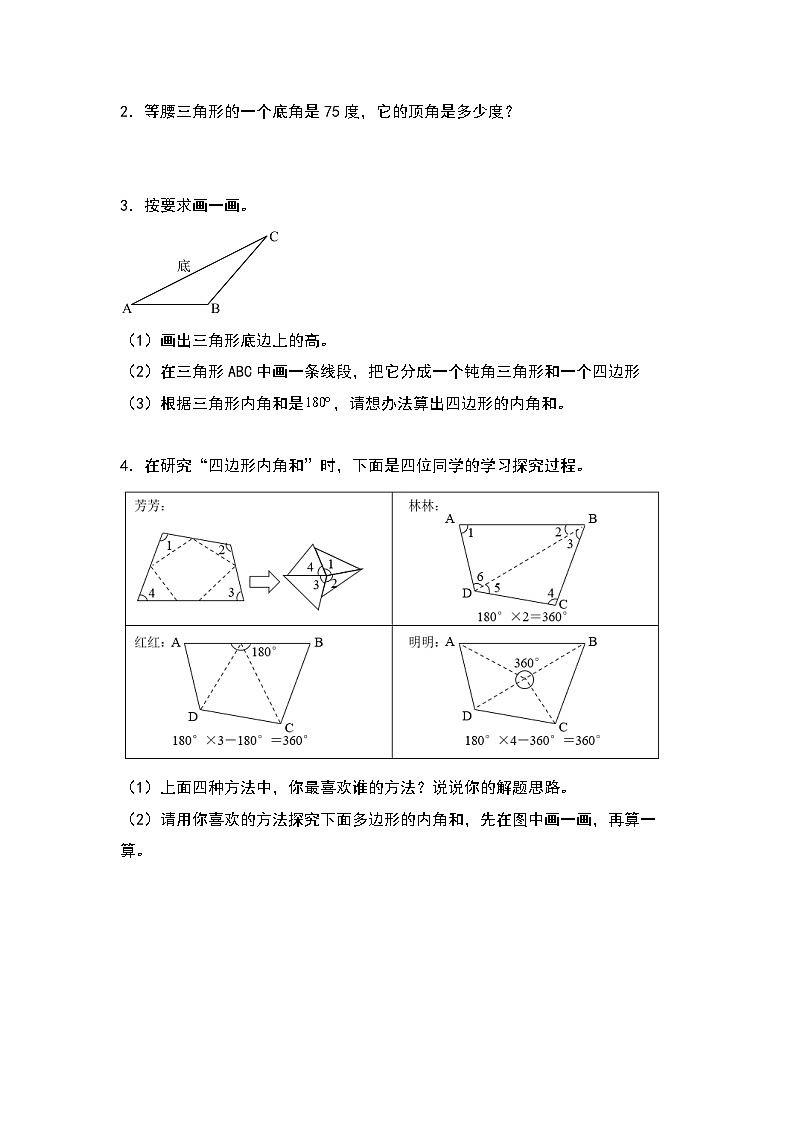
2．等腰三角形的一个底角是75度，它的顶角是多少度？

【答案】30度

【分析】根据等腰三角形的特征，两个底角相等，用75°×2即可计算出两个底角的度数，用180°减去两个底角的度数即可，据此解决。

【详解】180°－75°×2

＝180°－150°

＝30°

答：它的顶角是30度。

【点睛】解决本题的关键是熟练掌握等腰三角形的特征。

3．按要求画一画。

（1）画出三角形底边上的高。

（2）在三角形ABC中画一条线段，把它分成一个钝角三角形和一个四边形

（3）根据三角形内角和是，请想办法算出四边形的内角和。

【答案】（1）、（2）画图见详解

（3）360°；计算过程见详解

【分析】（1）从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底，依此画图。

（2）由四条边组成的封闭图形是四边形；有一个角是钝角的三角形是钝角三角形，依此分割；

（3）将四边形分成2个三角形，四边形的内角和等于2个三角形的内角和，依此解答。

【详解】（1）、（2）画图如下：

（3）分割如下图所示：

180°×2＝360°

答：四边形的内角和是360°。

【点睛】此题考查的是画三角形的高，平面图形的分割，以及四边形的内角和的计算，应熟练掌握。

4．在研究“四边形内角和”时，下面是四位同学的学习探究过程。

（1）上面四种方法中，你最喜欢谁的方法？说说你的解题思路。

（2）请用你喜欢的方法探究下面多边形的内角和，先在图中画一画，再算一算。

【答案】（1）林林的；思路见解析

（2）

540°

【分析】（1）根据自己的喜好，选出一个自己喜欢的方式，并说出解题思路即可。

（2）根据自己的喜好，先根据自己的方法画出图形，看看能分出几个三角形，每个三角形内角和都是180°，再列式计算即可。

【详解】（1）林林的，她把四边形分成了两个三角形，每个三角形的内角和都是180°，四边形是两个三角形组成则180°×2就是四边形的内角和360°。（答案不唯一）

（2）

3×180°＝540°

答：此多边形内角和是540°。（答案不唯一）

【点睛】此题考查了根据三角形内角和求多边形的内角和的过程和方法。

如图所示，两个三角形都是等腰三角形，求∠3的度数。

【答案】120°

【详解】180°-70°-25°-25°=60°　

∠3=180°-60°=120°

态度评定：

完成评定：

掌握评定：

  综合评定：