中考数学三轮冲刺《四边形》解答题冲刺练习12（含答案）

中考数学三轮冲刺《四边形》解答题冲刺练习12

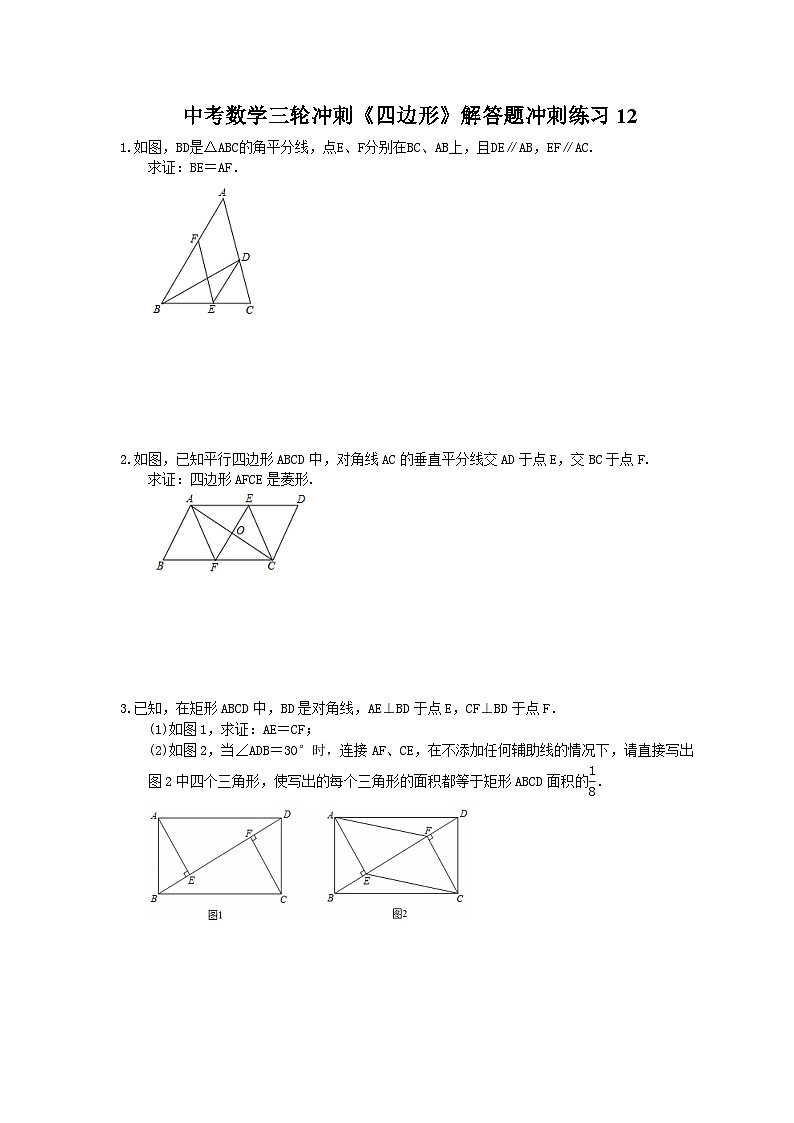
1.如图，BD是△ABC的角平分线，点E、F分别在BC、AB上，且DE∥AB，EF∥AC.

求证：BE＝AF．

2.如图，已知平行四边形ABCD中，对角线AC的垂直平分线交AD于点E，交BC于点F.

求证：四边形AFCE是菱形.

3.已知，在矩形ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F．

(1)如图1，求证：AE＝CF；

(2)如图2，当∠ADB＝30°时，连接AF、CE，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形ABCD面积的．

4.如图所示，四边形ABCD是平行四边形，AC、BD交于点O，∠1＝∠2．

(1)求证：四边形ABCD是矩形；

(2)若∠BOC＝120°，AB＝4cm，求四边形ABCD的面积．

5.如图，在△ABC中，AB＝BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．

求证：四边形BECD是矩形．

6.如图，是某城市部分街道示意图，AF∥BC，EC⊥BC，BA∥DE，BD∥AE，甲、乙两人同时从B站乘车到F站，甲乘1路车，路线是B⇒A⇒E⇒F；乙乘2路车，路线是B⇒D⇒C⇒F，假设两车速度相同，途中耽误时间相同，那么谁先到达F站，请说明理由.

7.如图，在▱ABCD中，DE平分∠ADC交AB于G，交CB的延长线于E，BF平分∠ABC交AD的延长线于F.

(1)若AD＝5，AB＝8，求GB的长；

(2)求证：∠E＝∠F.

8.如图，在▱ABCD中，对角线AC、BD相交于点O，点E在BD的延长线上，且△EAC是等边三角形.

（1）求证：四边形ABCD是菱形.

（2）若AC=8，AB=5，求ED的长.

9.如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC.设MN交∠ACB的角平分线于点E，交∠ACB的外角角平分线于点F.

(1)求证：OE＝OF；

(2)若CE＝12，CF＝5，求OC的长；

(3)当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由.

10.如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE.

(1)求证：CE＝AD；

(2)当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

(3)若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由.

0.中考数学三轮冲刺《四边形》解答题冲刺练习12（含答案）答案解析

一         、解答题

1.证明：∵DE∥AB，EF∥AC，

∴四边形ADEF是平行四边形，∠ABD＝∠BDE，

∴AF＝DE，

∵BD是△ABC的角平分线，

∴∠ABD＝∠DBE，

∴∠DBE＝∠BDE，

∴BE＝DE，

∴BE＝AF．

2.证明：∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠EAO＝∠FCO，

∵EF是AC的垂直平分线，

∴OA＝OC，AE＝CE，

在△AOE和△COF中，

，

∴△AOE≌△COF(ASA)，

∴OE＝OF，

∴四边形AFCE是平行四边形，

又∵AE＝CE，

∴四边形AFCE是菱形.

3.解：(1)∵四边形ABCD为矩形

∴AB∥CD且AB＝CD

∴∠ABE＝∠CDF

∵AE⊥BD

∴∠AEB＝90°

∵CE⊥BD

∴∠CFD＝90°

∴△ABE≌△CDF(AAS)

∴AE＝CF．

(2)△AFD，△ABE，△BEC，△FDC．

4.证明：(1)∵∠1＝∠2，

∴BO＝CO，即2BO＝2CO．

∵四边形ABCD是平行四边形，

∴AO＝CO，BO＝OD，

∴AC＝2CO，BD＝2BO，

∴AC＝BD．

∵四边形ABCD是平行四边形，

∴四边形ABCD是矩形；

(2)解：在△BOC中，∵∠BOC＝120°，

∴∠1＝∠2＝(180°﹣120°)÷2＝30°，

∴在Rt△ABC中，AC＝2AB＝2×4＝8(cm)，

∴BC＝4(cm)．

∴四边形ABCD的面积＝16cm2．

5.证明：∵AB＝BC，BD平分∠ABC，

∴BD⊥AC，AD＝CD．

∵四边形ABED是平行四边形，

∴BE∥AD，BE＝AD，

∴四边形BECD是平行四边形．

∵BD⊥AC，

∴∠BDC＝90°，

∴▱BECD是矩形．

6.解：可以同时到达.理由如下：连结BE交AD于G，

∵BA∥DE，AE∥DB，

∴四边形ABDE为平行四边形，

∴AB＝DE，AE＝BD，BG＝GE，

∵AF∥BC，G是BE的中点，

∴F是CE的中点，即EF＝FC，

∵EC⊥BC，AF∥BC，

∴AF⊥CE，即AF垂直平分CE，

∴DE＝DC，

∴AB＝DC，

∴AB＋AE＋EF＝DC＋BD＋CF，

∴二人同时到达F站.

7.解：(1)∵在▱ABCD中，DE平分∠ADC交AB于点G，

BF平分∠ABC交AD的延长线于F，

∴∠1＝∠2，∠3＝∠4，AB∥DC，

∴∠2＝∠AGD，

∴∠1＝∠AGD，

∴AD＝AG＝5．

∵AB＝8，

∴BG＝8﹣5＝3；

(2)证明：∵四边形ABCD是平行四边形，

∴∠ADC＝∠ABC，DC∥AB，AD∥BC．

∵DE平分∠ADC，

∴∠2＝∠ADC．

∵BF平分∠ABC，

∴∠4＝∠ABC，

∴∠2＝∠4．

∵DC∥AB，

∴∠AGD＝∠2，

∴∠AGD＝∠4，

∴ED∥FB．

∵AF∥CE，

∴四边形BFDE是平行四边形，

∴∠E＝∠F．

8.（1）证明：∵四边形ABCD是平行四边形，

∴AO=CO，

∵△EAC是等边三角形，

∴EA=EC，

∴EO⊥AC，

∴四边形ABCD是菱形；

（2）解：∵四边形ABCD是菱形，AC=8，

∴AO=CO=4，DO=BO，

在Rt△ABO中，BO==3，

∴DO=BO=3，

在Rt△EAO中，EO==4，

∴ED=EO﹣DO=4﹣3.

9.证明：(1)∵CF平分∠ACD，且MN∥BD，

∴∠ACF＝∠FCD＝∠CFO.

∴OF＝OC，

同理可证：OC＝OE，

∴OE＝OF.

(2)由(1)知：OF＝OC，OC＝OE，

∴∠OCF＝∠OFC，∠OCE＝∠OEC.

∴∠OCF＋∠OCE＝∠OFC＋∠OEC，

而∠OCF＋∠OCE＋∠OFC＋∠OEC＝180°，

∴∠ECF＝∠OCF＋∠OCE＝90°，

∴EF＝13.

∴OC＝EF＝6.5.

(3)当点O移动到AC中点时，四边形AECF为矩形.

理由：由(1)知OE＝OF，当点O移动到AC中点时有OA＝OC，

∴四边形AECF为平行四边形.

又∵∠ECF＝90°，

∴四边形AECF为矩形.

10.证明：(1)∵DE⊥BC，

∴∠DFB＝90°，

∵∠ACB＝90°，

∴∠ACB＝∠DFB，

∴AC∥DE，

∵MN∥AB，即CE∥AD，

∴四边形ADEC是平行四边形，

∴CE＝AD；

(2)解：四边形BECD是菱形，理由是：∵D为AB中点，

∴AD＝BD，

∵CE＝AD，

∴BD＝CE，

∵BD∥CE，

∴四边形BECD是平行四边形，

∵∠ACB＝90°，D为AB中点，

∴CD＝BD，

∴▱四边形BECD是菱形；

(3)当∠A＝45°时，四边形BECD是正方形，理由是：

∵∠ACB＝90°，∠A＝45°，

∴∠ABC＝∠A＝45°，

∴AC＝BC，

∵D为BA中点，

∴CD⊥AB，

∴∠CDB＝90°，

∵四边形BECD是菱形，

∴菱形BECD是正方形，

即当∠A＝45°时，四边形BECD是正方形.