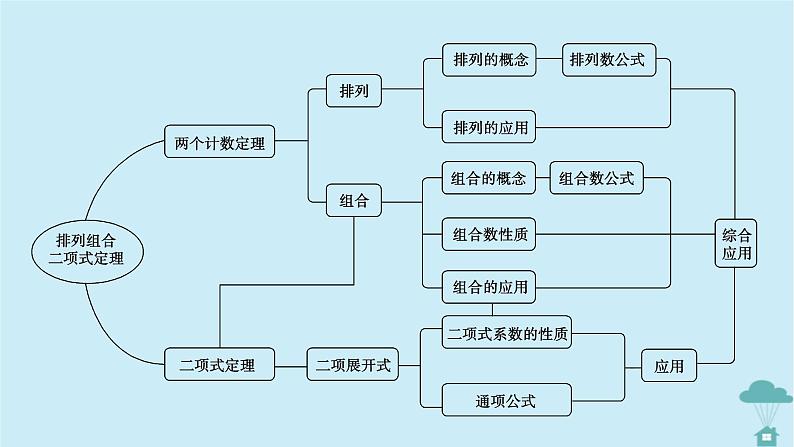
新教材2023年高中数学第六章计数原理章末知识梳理课件新人教A版选择性必修第三册

这是一份新教材2023年高中数学第六章计数原理章末知识梳理课件新人教A版选择性必修第三册，共35页。
第六章　计数原理章末知识梳理知识结构•理脉络 要点梳理•晰精华基本计数原理1．分类加法计数原理：N＝m1＋m2＋…＋mn.2．分步乘法计数原理：N＝m1×m2×…×mn.知识点1排列1．排列：一般地，从n个不同元素中，任取出m(m≤n，m，n∈N*)个元素，按照一定的顺序排成一列，称为从n个不同元素中取出m个元素的一个排列．知识点2组合1．组合：一般地，从n个不同元素中取出m(m≤n，m，n∈N*)个元素并成一组，称为从n个不同元素中取出m个元素的一个组合．知识点3二项式定理知识点4素养突破•提技能1．分类加法计数原理和分步乘法计数原理很少单独命题，多与排列、组合等问题相结合，以选择题或填空题的形式考查，难度适中，属中档题．2．应用两个原理解决有关计数问题的关键是区分事件是分类完成还是分步完成，而分类与分步的区别又在于任取其中某一方法是否能完成事件，能完成便是分类，否则便是分步．对于有些较复杂问题可能既要分类又要分步，此时，应注意层次分明，不重不漏． (2022·北京通州区高三期末)从数字1，2，3，4，5中取出3个数字(允许重复)，组成三位数，各位数字之和等于6，这样的三位数的个数为 (　　)A．7 B．9C．10 D．13典例1C[规律方法]　用两个计数原理解决实际问题时，往往从特殊元素入手，通过对其分析，展开讨论，将复杂问题分解为几类简单问题加以解决．求解排列组合综合问题的常用策略：(1)特殊元素优先安排的策略．(2)合理分类和准确分步的策略．(3)排列、组合混合问题先选后排的策略．(4)正难则反、等价转化的策略．(5)相邻问题捆绑处理的策略．(6)不相邻问题插空处理的策略．(7)定序问题除法处理的策略．(8)分排问题直排处理的策略．(9)“小集团”排列问题中先整体后局部的策略．(10)构造模型的策略．已知六人排成一排拍照，其中甲、乙、丙三人两两不相邻，甲、丁两人必须相邻，则满足要求的排队方法数为 (　　)A．72 B．96C．120 D．288典例2A在高三一班元旦晚会上，有6个演唱节目，4个舞蹈节目．(1)当4个舞蹈节目要排在一起时，有多少种不同的节目安排顺序？(2)当要求每2个舞蹈节目之间至少安排1个演唱节目时，有多少种不同的节目安排顺序？(3)若已定好节目单，后来情况有变，需加上诗朗诵和快板2个节目，但不能改变原来节目的相对顺序，有多少种不同的节目演出顺序？典例3[规律方法]　解决排列组合的综合问题时，通常都是从特殊元素、特殊位置入手，先安排特殊元素、特殊位置，再安排其他元素、其他位置，根据分步乘法计数原理解决问题．对于二项式定理的考查常出现两类问题：一类是直接运用通项公式来求特定项；另一类需要运用转化思想化为二项式定理来处理问题．从近几年高考命题趋势来看，对于本部分知识的考查以基础知识和基本技能为主，难度不大，但不排除与其他知识交汇，具体归纳如下：(1)考查通项公式问题．(2)考查系数问题：①涉及项的系数、二项式系数以及系数的和．②一般采用通项公式或赋值法解决．③可转化为二项式定理解决问题．(x＋y)(2x－y)5的展开式中x3y3的系数为 (　　)A．－80 B．－40C．40 D．80典例4C典例5已知(x＋2)(2x－1)5＝a0＋a1x＋a2x2＋…＋a6x6，则a0＋a2＋a4＝ (　　)A．123 B．91C．－152 D．－120[解析]　(x＋2)(2x－1)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5＋a6x6中，取x＝1，得a0＋a1＋a2＋a3＋a4＋a5＋a6＝3，取x＝－1，得a0－a1＋a2－a3＋a4－a5＋a6＝－243，所以2(a0＋a2＋a4＋a6)＝－240，即a0＋a2＋a4＋a6＝－120，又a6＝32，则a0＋a2＋a4＝－152.典例6C[规律方法]　解决二项式系数和问题的思维过程如下：解决两个计数原理的综合应用问题时，很多时候都需要既分类又分步才能完成．解题时，先根据问题分析是先分类还是先分步．对于先分类后分步的题目，应明确分类的标准，做到不重不漏；对于先分步后分类的题目，往往是一个元素的位置选择对另一个元素的位置选择有影响．(2021·四川绵阳)现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这3张卡片中至多有两张红色卡片，并且其余卡片颜色不能相同，那么不同取法的种数为______. (用数字作答)[解析]　根据题意，分3种情况讨论：①取出的3张卡片中有2张红色的，需要在其他三种颜色的卡片中任选1张，典例7328[规律方法]　寻找合理的分类方法是解此类题目的关键．对于计数问题，分类的依据主要是特殊元素或特殊位置．排列组合与二项式定理中的许多问题，往往是同一数学模型的不同体现，可以利用等价转化的思想，转化为计数原理中的基本模型，再利用排列与组合知识列式解决问题．现将10个参加全国高中数学联赛的名额分配给某地区四个不同的学校，要求一个学校1名，一个学校2名，一个学校3名，一个学校4名，则不同的分配方案有 (　　)A．4种 B．24种C．96种 D．12 600种典例8B[规律方法]　联赛的名额虽然是不加区分的，可视为相同的元素，但由于各校所分的名额数各不相同，因此可认为该分配问题是四个不同元素的全排列问题．