初中数学苏科版八年级上册3.1 勾股定理教学课件ppt

这是一份初中数学苏科版八年级上册3.1 勾股定理教学课件ppt，共17页。PPT课件主要包含了知识要点，勾股定理与网格，练一练等内容，欢迎下载使用。

1.勾股定理与数轴、坐标系
3.勾股定理与几何图形
我们知道数轴上的点有的表示有理数，有的表示无理数，你能在数轴上画出表示 的点吗？ 如果能画出长为 的线段，就能在数轴上画出表示 的点.容易知道，长为 的线段是两条直角边的长都为1的直角三角形的斜边.长为 的线段能是直角边的长为正整数的直角三角形的斜边吗？
利用勾股定理，可以发现，直角边的长为正整数2, 3的直角三角形的斜边长为 .由此，可以依照如下方法在数轴上画出表示 的点. 如图,在数轴上找出表示3的点A， 则OA=3,过点A作直线l垂直于OA，在l上取点B，使AB = 2,以原点O为圆心，以OB为半径作弧，弧与数轴的交点C即为表示 的点.
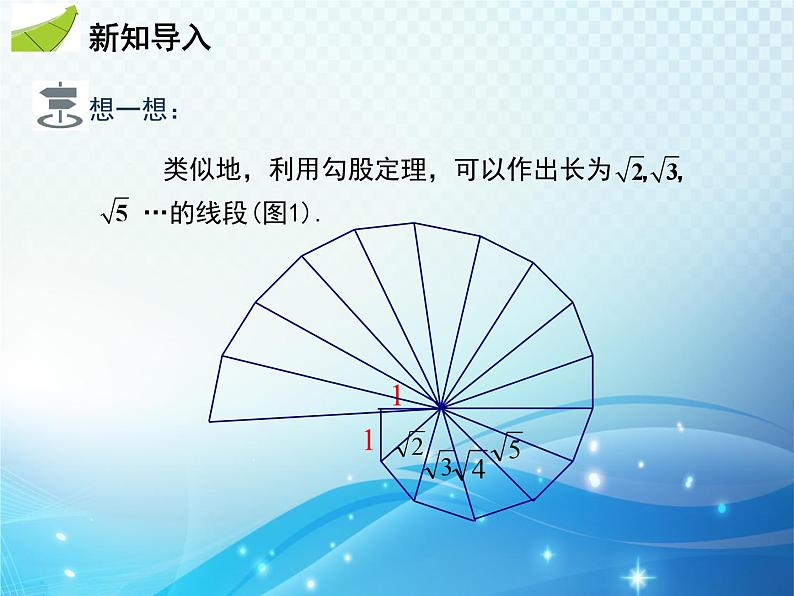
类似地，利用勾股定理，可以作出长为 …的线段(图1).
在数轴上做出表示 的点.
如图所示．作法：(1)在数轴上找出表示4的点A，则OA＝4；(2)过A作直线l垂直于OA；(3)在直线l上取点B，使AB＝1；(4)以原点O为圆心，以OB为半径作弧，弧与 数轴的交点C即为表示 的点．
如图，在平面直角坐标系中，点P的坐标为(-2，3)，以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于(　　) A．-4和-3之间 B．3和4之间 C．-5和-4之间 D．4和5之间
如图是由4个边长为1的正方形构成的“田字格”，只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段_____条．
如图，在2×2的方格中，小正方形的边长是1，点A，B，C都在格点上，求AB边上的高.
解：如图，过点C作CD⊥AB于点D.
归纳：1.勾股定理与网格的综合求线段长时，通常是把线段放在与网格构成的直角三角形中，利用勾股定理求其长度.2.网格中求格点三角形的高的题，常用的方法是利用网格求面积，再用面积法求高.
例 如图，在△ABC中，∠C＝60°，AB＝14，AC＝10. 求BC的长．
解：如图，过点A作AD⊥BC于D.∵∠ADC＝90°，∠C＝60°，∴CD＝ AC＝5.在Rt△ACD中，AD在Rt△ABD中，BD∴BC＝BD＋CD＝11＋5＝16.
如图，折叠长方形ABCD的一边AD，使点D落在BC边的F点处，若AB=8 cm，BC=10 cm，求EC的长.
解：在Rt△ABF中,由勾股定理得 BF2=AF2－AB2=102－82=36，∴BF=6 cm.∴CF=BC－BF=4.设EC=x cm，则EF=DE=(8－x) cm ，在Rt△ECF中,根据勾股定理得 x2+ 42=(8－x)2，解得 x=3.
即EC的长为3 cm.
如图，点C表示的数是(　　) A．1 B. C．1.5 D.
2.如图，每个小正方形的边长均为1，则△ABC中， 长为无理数的边有(　　) A．0条 B．1条 C．2条 D．3条
3.如图是一张直角三角形的纸片，两直角边AC＝ 6 cm，BC＝8 cm，现将△ABC折叠，使点B与点 A重合，折痕为DE，则BE的长为(　　) A．4 cm B．5 cm C．6 cm D．10 cm
4.如图，把长方形纸条ABCD沿EF，GH同时折叠，B，C两点恰好落在AD边的P点处，若∠FPH＝90°，PF＝8，PH＝6，则长方形ABCD的面积为________．