河北省唐山市滦州市2022-2023学年八年级下学期期中数学试题(含答案)

滦州市2022—2023学年度第二学期期中考试

八年级数学试卷

注意事项：1.本试卷共4页，总分100分.

2.选择题答案用2B铅笔涂在答题纸上.

3.非选择题须用0.5毫米黑色中性笔书写在答题纸上.

一、选择题：（本大题有16个小题，共42分. 1～10小题各3分，11～16小题各2分. 在每小题给出的四个选项中，只有一项是符合题目要求的）

1.如图，B地在A地的（   ）

A.北偏东，相距200m处    B.北偏西，相距200m处

C.南偏西，相距200m处    D.北偏东，相距200m处

2.函数的自变x的取值范围是（   ）

A.    B.    C.    D. 且

3.下列函数中，y是x的一次函数的是（   ）

A.   B.    C.    D.

4.已知两个变量之间的关系满足，则当时，对应的y的值（   ）

A. 3     B. 1     C.     D.

5.第二象限的点P到x轴距离为2，到y轴距离为3. 则P点坐标为（   ）

A.    B.    C.    D.

6.下列图象中，表示y是x的函数的个数有（   ）

A. 1个    B. 2个    C. 3个    D. 4个

7.汽车以60千米/时的速度在公路上匀速行驶，1小时后进入高速路，继续以100千米/时的速度匀速行驶，则汽车行驶的路程s（千米）与行驶的时间t（时）的函数关系的大致图象是（   ）

A.   B.   C.   D.

8.若点在x轴上，则a的值是（   ）

A.     B. 3     C.     D. 4

9.已知y与成正比例，并且时，，那么y与x之间的函数关系式为（   ）

A.    B.   C.   D.

10.在平面直角坐标系中，点A的坐标为，点B的坐标为，下列说法不正确的是（   ）

A.点A在第三象限      B. 点B在第二、四象限的角平分线上

C.线段AB平行于x轴      D. 点A与点B关于y轴对称

11.已知点，，都在直线上，则，，的大小关系是（   ）

A.   B.   C.   D.

12.一次函数的图象经过点P，且，则点P的坐标不可能为（   ）

A.    B.    C.    D.

13.如图，在平面直角坐标系中，，点P是线段AB上的一个动点，则OP的最小值是（   ）

A.     B.     C. 4     D. 3

14.将直线通过平移得到直线，平移的方式为（   ）

A.向左平移3个单位长度     B.向右平移3个单位长度

C.向下平移3个单位长度     D.向上平移3个单位长度

15.若等腰三角形的周长是80cm，则能反映这个等腰三角形的腰长y cm与底边长x cm的函数关系式的图象是（   ）

A.  B.  C.  D.

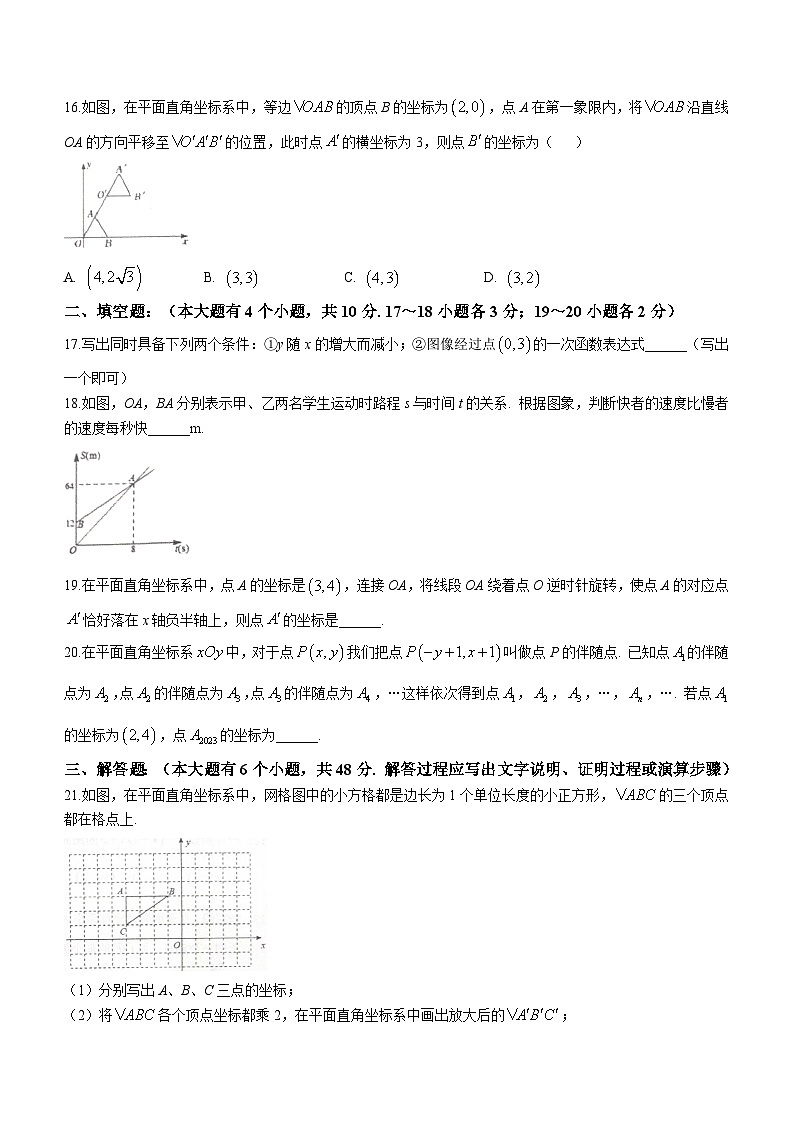
16.如图，在平面直角坐标系中，等边的顶点B的坐标为，点A在第一象限内，将沿直线OA的方向平移至的位置，此时点的横坐标为3，则点的坐标为（   ）

A.   B.    C.    D.

二、填空题：（本大题有4个小题，共10分. 17～18小题各3分；19～20小题各2分）

17.写出同时具备下列两个条件：①y随x的增大而减小；②图像经过点的一次函数表达式______（写出一个即可）

18.如图，OA，BA分别表示甲、乙两名学生运动时路程s与时间t的关系. 根据图象，判断快者的速度比慢者的速度每秒快______m.

19.在平面直角坐标系中，点A的坐标是，连接OA，将线段OA绕着点O逆时针旋转，使点A的对应点恰好落在x轴负半轴上，则点的坐标是______.

20.在平面直角坐标系中，对于点我们把点叫做点P的伴随点. 已知点的伴随点为，点的伴随点为，点的伴随点为，…这样依次得到点，，，…，，…. 若点的坐标为，点的坐标为______.

三、解答题：（本大题有6个小题，共48分. 解答过程应写出文字说明、证明过程或演算步骤）

21.如图，在平面直角坐标系中，网格图中的小方格都是边长为1个单位长度的小正方形，的三个顶点都在格点上.

（1）分别写出A、B、C三点的坐标；

（2）将各个顶点坐标都乘2，在平面直角坐标系中画出放大后的；

（3）直接写出两个三角形的面积关系：______.

22.小华骑自行车上学，当他骑了一段路时，想起要买本书，于是又折回到刚经过的某书店，买到书后继续去学校，以下是他本次上学所用的时间与离家距离的关系示意图，根据图中提供的信息回答下列问题：

（1）小华家到学校的路程是______米，小华在书店停留了____分钟.

（2）本次上学途中，小华一共骑行了______米？

（3）通过计算说明在整个上学的途中哪个时间段小华的骑车速度最快？最快的速度是多少？

23.如图，直线的图象与y轴交于点A，直线的图象与y轴交于点B，两者相交于点C.

（1）方程组的解是______；

（2）当与同时成立时，x的取值范围为______.

（3）求的面积.

24.如图，直线与x轴交于点A，点也在该直线上，点B关于x轴的对称点为点C，直线BC交x轴于点D，点E坐标为.

（1）m的值为______，点C的坐标为______；

（2）求直线AC的函数表达式；

（3）晶晶有个想法：“设. 由点B与点C关于x轴对称易得，而与四边形DCEO拼接后可看成，这样求S便转化为直接求的面积．”晶晶的想法对吗？

25.某服装店同时购进甲、乙两种款式的运动服共300套，进价和售价如表中所示，设购进甲款运动服x套（x为正整数），该服装店售完全部甲、乙两款运动服获得的总利润为y元.

（1）求y与x的函数关系式；

（2）该服装店计划投入2万元购进这两款运动服，则至少购进多少套甲款运动服？若售完全部的甲、乙两款运动服，则服装店可获得的最大利润是多少元？

（3）在（2）的条件下，若服装店购进甲款运动服的进价降低a元（其中），且最多购进240套甲款运动服，若服装店保持这两款运动服的售价不变，则购进甲款运动服多少件使该服装店获利最大（直接写出结果）.

26.如图，长方形ABCD中，长cm，宽cm，动点P在折线上从A向C移动（点P不与点C重合），设点P运动的路径长为x cm，的面积为y .

（1）当点P在AD上运动时，的面积_______，当点P在DC上运动时，的面积__________（填“增大”“减小”或“或“不变”）

（2）求y关于x的函数表达式，并指出自变量x的取值范围；

（3）当_________时，为等腰三角形.

河北省唐山市滦州市2022-2023学年

八年级下学期5月期中数学试题答案

一、选择题

1-16 BCCBBBCCBDADBCDA

二、填空题

17.（答案不唯一）

18. 1.5米

19.

20.

三、解答题

21.（1）如图，即为所求.

（2）点，，，

点，，

如图，

（3）设点P的坐标为，

的面积为，，

解得或7，

点P的坐标为或

22.解：（1）由图可得，学校的纵坐标为1500，小明家的纵坐标为0，故小明家到学校的路程是1500米.

（2）根据题意，小明在书店停留的时间为从8分到12分，故小明在书店停留了4分钟.

（3）读图可得：小明共行驶了（米），一共用了14分钟.

（4）由图可得，时，直线最陡，故小明在12～14分钟骑车速度最快，速度为 （米/分）.

23.（1）由题图知，两条直线的交点坐标为，

方程组的解为，故答案为.

（2）由题图知，当与同时成立时，x取值范围. 故答案为.

（3）令，则，，，.

.

.

24.（1）点在直线上，

；.

点B关于x轴的对称点为点C，.

故答案为：，；

（2）直线与x轴交于点A，，

设直线AC的函数关系式为，由题意得，

解得

直线AC的函数表达式为：

（3）由（2）直线AC的函数表达式为.

令，得.

直线AC与y轴的交点坐标为

而点E坐标为，

点E不在直线AC上，即点A、C、E不在同一条直线上.

.

25. （1）根据题意得；

即.

（2）由题意得，，解得，

至少要购进甲款运动服200套.

又，，y随x的增大而减小，

当时，y有最大值，，

若售完全部的甲、乙两款运动服，则服装店可获得的最大利润是15000元.

（3）由题意得，，其中，

化简得，，，则：

①当时，，y随x的增大而减小，

当时，y有最大值，

则服装店应购进甲款运动服200套、乙款运动服100套，获利最大.

②当时，，，则服装店应购进甲款运动服的数量应满足，且x为整数时，服装店获利最大.

③当时，，y随x的增大而增大，

当时，y有最大利润，则服装店应购进甲款运动服240套、乙款运动服60套，获利最大.

26. （1）当点P在线段AD上时，的底为BC，高为CD，的面积不变；

当点P在线段CD上时，的底为BC，高为CP，的面积减小；

故答案为：不变，减小；

（2）由（1）知，当点P在线段AD上时，即时，

，

当点P在DC边上运动时，即，高在DC边上，即为CP，

综上所述，；

（3）分三种情况：当时，，此时；

当时，点P位于AD的中点，此时；

当时，，此时.

综上所述，当或5或8时，为等腰三角形.