


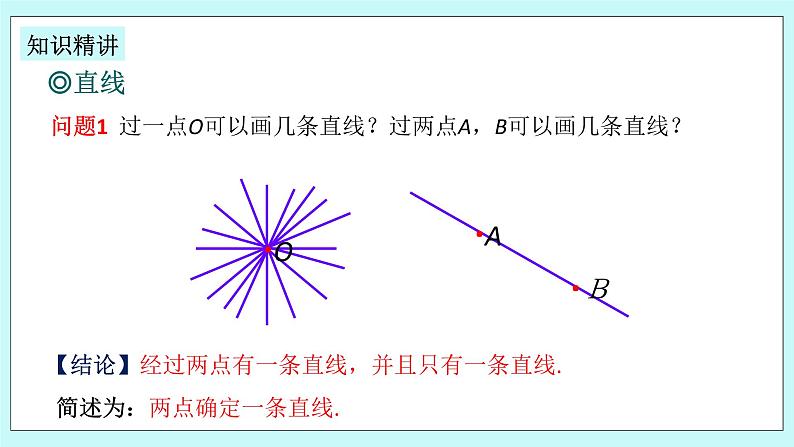






浙教版数学七上 6.2 线段、射线和直线 课件+练习
展开6.2 线段、射线、直线
一.选择题
1.平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,则平面内不重合的7个点最多可以确定的直线条数是
A.42 B.35 C.30 D.21
2.下列说法不正确的有
①绝对值是本身的数是正数;
②符号不同的两个数互为相反数;
③两数相加,和一定大于任何一个加数;
④线段和线段表示的是同一条线段.
A.①③ B.②③ C.①②③ D.①②④
3.如图,图中共有 条线段.
A.1 B.2 C.3 D.4
4.如图,点,,,,,在同一条直线上,则图中线段和射线的条数分别为
A.10,10 B.12,15 C.15,12 D.15,15
5下列语句中准确规范的是
A.直线,相交于一点 B.反向延长直线
C.反向延长射线是端点) D.延长线段到,使
6.如图,是一段高铁行驶路线图图中字母表示的5个点表示5个车站在这段路线上往返行车,需印制 种车票.
A.10 B.11 C.20 D.22
二.填空题
7.整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌便整整齐齐摆在了一条线上,这其中蕴含的数学道理是 .
8.往返于甲、乙两地的列车,中途需要停靠4个车站,如果每两站的路程都不相同,问:
(1)这两地之间有 种不同的票价;
(2)要准备 种不同的车票.
9.平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线 条.
10.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
11.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
12.已知线段,在上逐一画点(所画点与、不重合),当线段上有1个点时,共有3条线段,当线段上有2个点时,共有6条线段;当线段上有3个点时,共有10条线段;直接写出当线段上有20个点时,共有线段 条.
三.解答题
13.如图,已知点、、.,根据下列语句画图.(不写作图过程)
作射线、直线,连接并延长线段.
14.用适当的语句表述图中点与直线的关系.(至少4句)
15.已知平面上点,,,(每三点都不在一条直线上).
(1)经过这四点最多能确定 条直线.
(2)如图这四点表示公园四个地方,如果点,在公园里湖对岸两处,,在湖面上,要从到筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
16.作图题:如图,已知平面上四点,,,.
(1)画直线;
(2)画射线,与直线相交于;
(3)连结,相交于点.
17.(1)观察思考:如图,线段上有两个点、,请分别写出以点、、、为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
18. 经过顶点的一条直线,.,分别是直线上两
点,且.
(1)若直线经过的内部,且,在射线上,请解决下面两个问题:
①如图1,若,,则 ; (填“”,“”或“”;
②如图2,若,请添加一个关于与关系的条件 ,使①中的两个结论仍然成立.
(2)如图3,若直线经过的外部,,请提出,,三条线段数量关系的合理猜想并给出理由.
参考答案
一.选择题
1.【解答】解:两点确定1条直线;
不同三点最多可确定3条直线;
不同4点最多可确定条直线;
不同5点最多可确定条直线;
所以平面上不同的7个点最多可确定条直线.
故选:.
2.【解答】解:①绝对值是本身的数是非负数,故①符合题意;
②符号不同的两个数不一定是互为相反数,故②符合题意;
③两数相加,和不一定大于任何一个加数,故③符合题意;
④线段和线段表示的是同一条线段,故④不符合题意,
故选:.
3.【解答】解:图中共有3条线段:线段、、.
故选:.
4.【解答】解:图中线段有15条:线段、线段、线段、线段、线段、线段、线段、线段、线段、线段、线段、线段、线段,线段、线;
以每个点为端点的射线有2条,共6个点,故射线有12条;
故选:.
5.【解答】解:.点应该用大写字母表示,直线,相交于一点,故本选项错误;
.直线向两端无限延伸,可以反向延长射线,故本选项错误
.反向延长射线(应该是端点),故本选项错误
.可以延长线段到,使,本选项正确;
故选:.
6.【解答】解:,
故选:.
二.填空题
7.【解答】解:根据两点确定一条直线.
故答案为:两点确定一条直线.
8.【解答】解:(1)如图:
根据线段的定义:可知图中共有线段有,,,,,、,、、,、、,,共15条,有15种不同的票价;
(2)因车票需要考虑方向性,如,“”与“”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
9.【解答】解:①当四点共线时,则经过每两个点画一条直线,那么共可以画直线1条;
②当只有三点共线时,则经过每两个点画一条直线,那么共可以画直线4条;
③当每三点不共线时,则经过每两个点画一条直线,那么共可以画直线6条.
故答案为:1或4或6.
10.【解答】解:能解释这一实际应用的数学知识是:两点确定一条直线,
故答案为:两点确定一条直线.
11.【解答】解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
12.【解答】解:由题意可得:当在上有20个点时,共有线段:,
故答案为:231.
三.解答题
13.【解答】解:作射线、直线,连接并延长线段,如图所示:
14.【解答】解:点在直线上,点在直线上,直线经过、两点,点在直线外.
15.【解答】解:(1)经过这四点最多能确定6条直线:直线,直线,直线,直线,直线,直线,
故答案为:6;
(2)从节省材料的角度考虑,应选择图中路线2;如果有人想在桥上较长时间观赏湖面风光,应选择路线1,
因为两点之间,线段最短,路线2比路线1短,可以节省材料;而路线1较长,可以在桥上较长时间观赏湖面风光.
16.【解答】解:(1)(2)(3)如图所示:
17.【解答】解:(1)以点为左端点向右的线段有:线段、、,
以点为左端点向右的线段有线段、,
以点为左端点的线段有线段,
共有条线段;
(2)设线段上有个点,该线段上共有线段条,
则,
倒序排列有,
,
;
(3)把45位同学看作直线上的45个点,每两位同学之间的一握手看作为一条线段,
直线上45个点所构成的线段条数就等于握手的次数,
因此一共要进行次握手.
18.【解答】解:(1)①如图1中,
点在点的左侧,
,,,
,
,,
,
在和中,
,
,
,,
,
当在的右侧时,同理可证,
;
②时,①中两个结论仍然成立;
证明:如图2中,
,,
,
在和中,
,
,
,,
,
当在的右侧时,同理可证,
;
故答案为.
(2)结论:.
理由:如图3中,
,,
又,,
,
,
在和中,
,
,
,,
,
.
故答案为:,;②时.









