2023年中考数学三轮冲刺考前查漏补缺《相似三角形》(提高版)(含答案)
展开2023年中考数学三轮冲刺考前查漏补缺
《相似三角形》(提高版)
一 、选择题
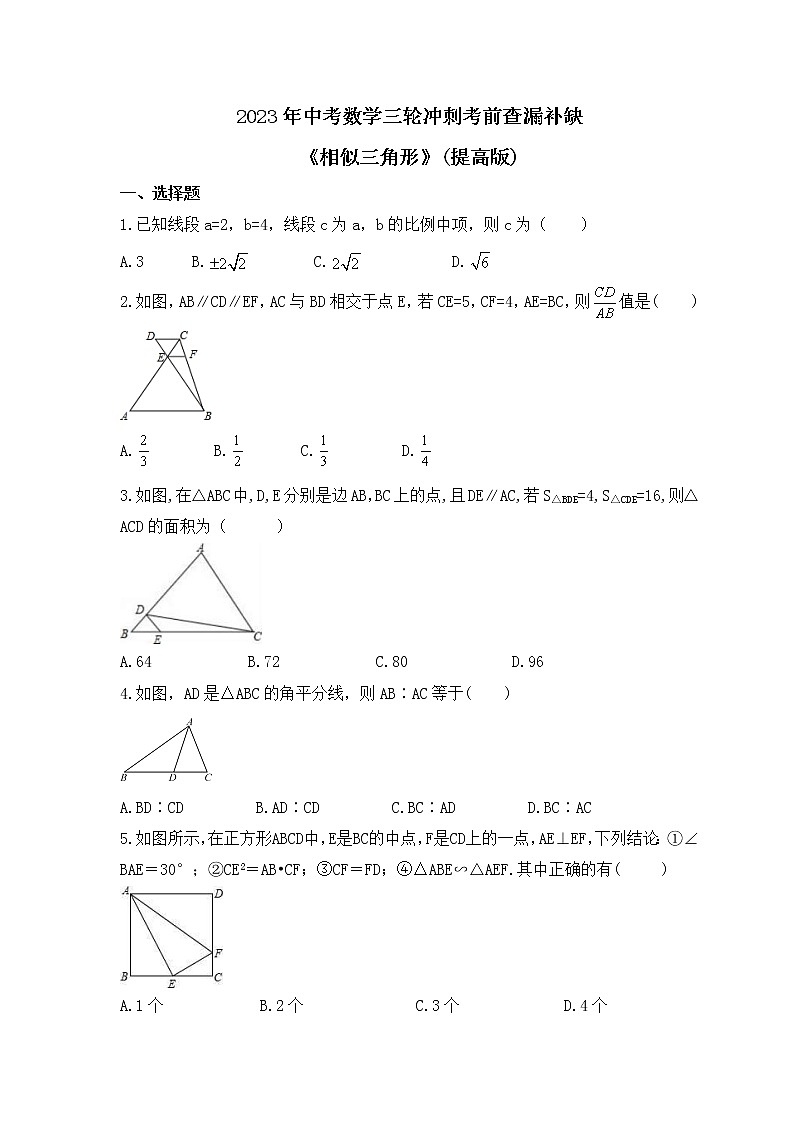
1.已知线段a=2,b=4,线段c为a,b的比例中项,则c为( )
A.3 B. C. D.
2.如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则值是( )
A. B. C. D.
3.如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
A.64 B.72 C.80 D.96
4.如图,AD是△ABC的角平分线,则AB∶AC等于( )
A.BD∶CD B.AD∶CD C.BC∶AD D.BC∶AC
5.如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,△ABC是面积为18cm2的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为( )
A.4cm2 B.6cm2 C.8cm2 D.10cm2
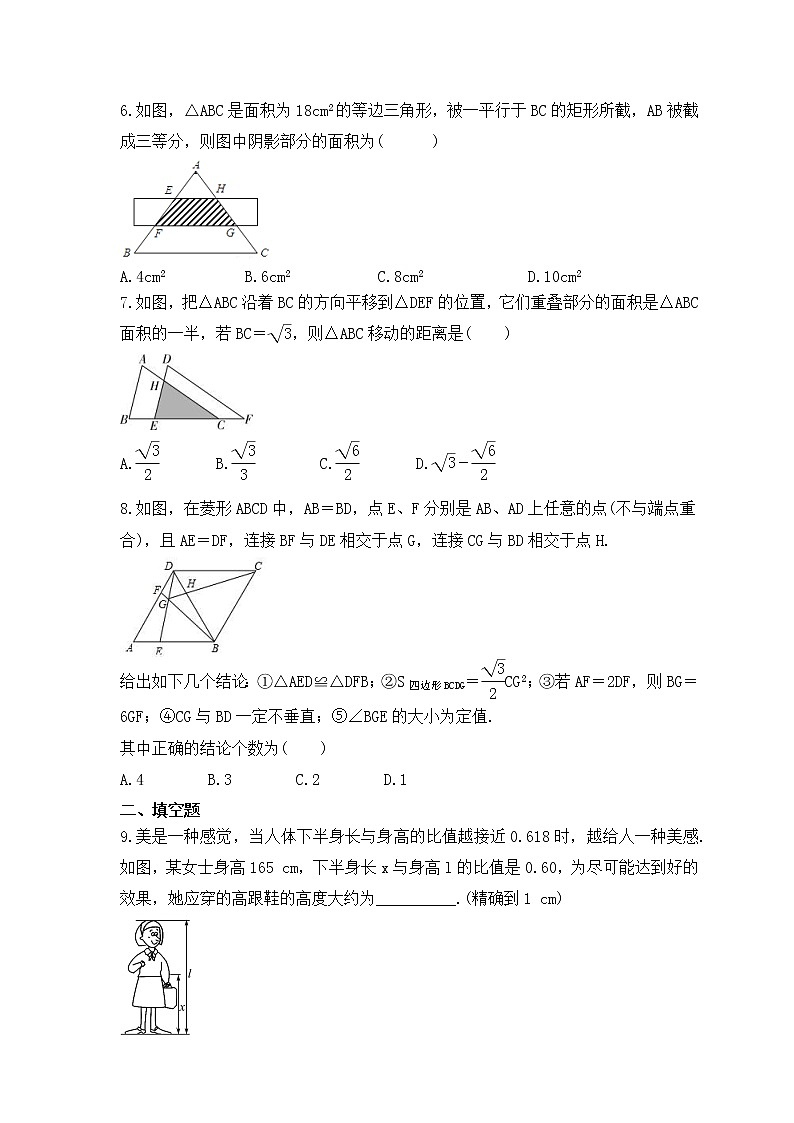
7.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=,则△ABC移动的距离是( )
A. B. C. D.-
8.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.
给出如下几个结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
其中正确的结论个数为( )
A.4 B.3 C.2 D.1
二 、填空题
9.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165 cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为__________.(精确到1 cm)
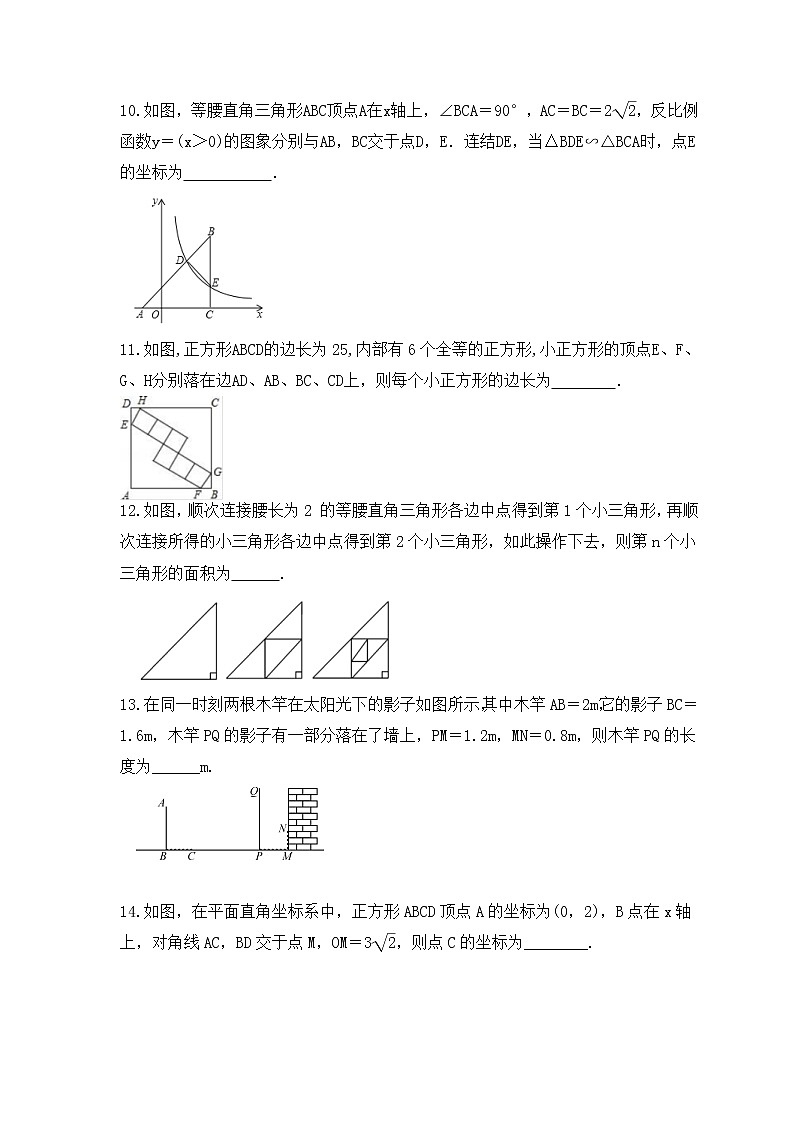
10.如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2,反比例函数y=(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为 .
11.如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为 .
12.如图,顺次连接腰长为2 的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,如此操作下去,则第n个小三角形的面积为 .
13.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为______m.
14.如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,2),B点在x轴上,对角线AC,BD交于点M,OM=3,则点C的坐标为________.
三 、解答题
15.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= °.
(2)如图,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
16.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
17.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.连接CM交DB于N.
(1)求证:BD2=AD•CD;
(2)若CD=6,AD=8,求MN的长.
18.如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BH•CH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?
19.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BC=AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
20.为了改善市民的生活环境,我市在某河滨空地处修建一个如图所示的休闲文化广场.在Rt△ABC内修建矩形水池DEFG,使顶点D、E在斜边AB上,F、G分别在直角边BC、AC上;又分别以AB、BC、AC为直径作半圆,它们交出两弯新月(图中阴影部分),两弯新月部分栽植花草;其余空地铺设地砖.其中AB=24米,∠BAC=60°.设EF=x米,DE=y米.
(1)求y与x之间的函数解析式;
(2)当x为何值时,矩形DEFG的面积最大?最大面积是多少?
(3)求两弯新月(图中阴影部分)的面积,并求当x为何值时,矩形DEFG的面积等于两弯新月面积的?
参考答案
1.B
2.C
3.D
4.A
5.C.
6.B
7.D.
8.B.
9.答案为:8 cm
10.答案为:(,).
11.答案为:.
12.答案为:.
13.答案为:2.3.
14.答案为:(6,4).
15.解:(1)当AD=CD时,如图,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)由已知AC=AD=2,
∵△BCD∽△BAC,
∴=,
设BD=x,
∴()2=x(x+2),
∵x>0,
∴x=﹣1,
∵△BCD∽△BAC,
∴==
16.解:设运动了ts,根据题意得:AP=2tcm,CQ=3tcm,
则AQ=AC﹣CQ=16﹣3t(cm),
当△APQ∽△ABC时,,
即,解得:t=;
当△APQ∽△ACB时,,即,
解得:t=4;
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是:s或4s.
17.证明:(1)∵DB平分∠ADC,
∴∠ADB=∠CDB,且∠ABD=∠BCD=90°,
∴△ABD∽△BCD
∴
∴BD2=AD•CD
(2)∵BM∥CD∴∠MBD=∠BDC
∴∠ADB=∠MBD,且∠ABD=90°
∴BM=MD,∠MAB=∠MBA
∴BM=MD=AM=4
∵BD2=AD•CD,且CD=6,AD=8,
∴BD2=48,
∴BC2=BD2﹣CD2=12
∴MC2=MB2+BC2=28
∴MC=2
∵BM∥CD∴△MNB∽△CND
∴,且MC=2
∴MN=
18.(1)证明:∵CE⊥BF,GH⊥BC,
∴∠CGB=∠CHG=∠BHG=90°,
∴∠CGH+∠BGH=90°,∠BGH+∠GBH=90°,
∴∠CGH=∠GBH,
∴△CGH∽△GBH,
∴=,
∴GH2=BH•CH;
(2)解:作EM⊥CB交CB的延长线于M.设CH=x,HB=y.
则有,解得或,
∵∠ABC是钝角,
∴CH>BH,
∴CH=18,BH=2,
∵G是△ABC的重心,∴CG=2EG,
∵GH⊥BC,EM⊥BC,
∴GH∥EM,
∴==,
∴EM=9,CM=27,
∴BM=CM﹣BC=7,
∴BE=,
∴AB=2BE=2.
19.解:(1)∵OA=OC,∴∠A=∠ACO,
∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线
(2)∵PC=AC,
∴∠A=∠P,∴∠A=∠ACO=∠PCB=∠P,
∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠CBO=∠COB,
∴BC=OC,
∴BC=AB
(3)连结MA,MB,∵点M是弧AB的中点,
∴=,∴∠ACM=∠BCM,
∵∠ACM=∠ABM,
∴∠BCM=∠ABM,
∵∠BMC=∠NMB,
∴△MBN∽△MCB,
∴=,
∴BM2=MC·MN,
∵AB是⊙O的直径,=,
∴∠AMB=90°,AM=BM,
∵AB=4,
∴BM=2,
∴MC·MN=BM2=8.
20.解:(1)在Rt△ABC中,由题意得AC=12米,BC=36米,∠ABC=30°,
所以AD===x,BE==x,
又AD+DE+BE=AB,
所以y=24﹣x﹣x=24﹣x(0<x<18).
(2)矩形DEFG的面积S=xy=x(24﹣x)
=﹣x2+24x
=﹣(x﹣9)2+108.
所以当x=9时,矩形DEFG的面积最大,最大面积为108平方米.
(3)记AC为直径的半圆、BC为直径的半圆、AB为直径的半圆面积分别为S1、S2、S3,
两弯新月面积为S,则S1=πAC2,S2=πBC2,S3=πAB2,
由AC2+BC2=AB2可知S1+S2=S3,
∴S1+S2﹣S=S3﹣S△ABC,故S=S△ABC,
所以两弯新月的面积S=×12×36=216(平方米),
由﹣(x﹣9)2+108=×216,即(x﹣9)2=27,
解得x=9±3,符合题意,
所以当x=(9±3)米时,矩形DEFG的面积等于两弯新月面积的.
2023年中考数学三轮冲刺考前查漏补缺《整式》(提高版)(含答案): 这是一份2023年中考数学三轮冲刺考前查漏补缺《整式》(提高版)(含答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年中考数学三轮冲刺考前查漏补缺《圆》(提高版)(含答案): 这是一份2023年中考数学三轮冲刺考前查漏补缺《圆》(提高版)(含答案),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年中考数学三轮冲刺考前查漏补缺《实数》(提高版)(含答案): 这是一份2023年中考数学三轮冲刺考前查漏补缺《实数》(提高版)(含答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












