


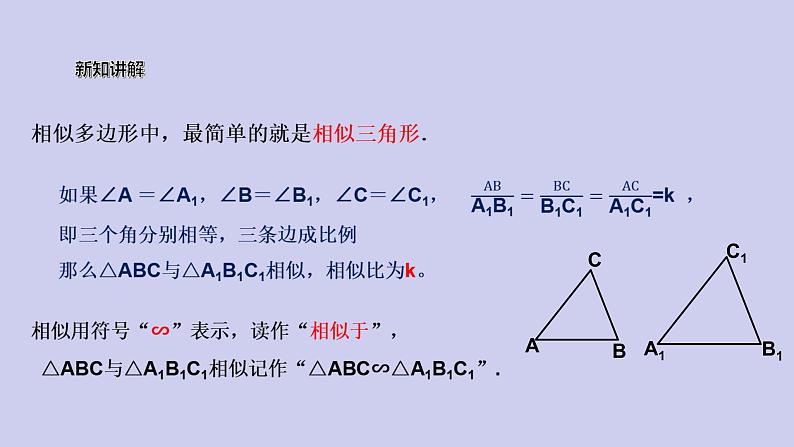

初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定备课ppt课件
展开1. 了解相似三角形的概念;2. 掌握平行线分线段成比例定理的基本事实、推论以及利用平行线法判定三角形相似;3. 应用平行线分线段成比例定理及平行线法判定三角形相似来解决问题;4.经历平行线分线段成比例的认识过程,得到利用平行线法判定三角形相似的方法。
1.相似多边形的特征是什么?2.怎样判定两个多边形相似?3.什么叫相似比?
相似多边形对应边的比叫做相似比.
相似多边形的对应角相等,对应边成比例。
对应角相等,对应边成比例的多边形是相似多边形。
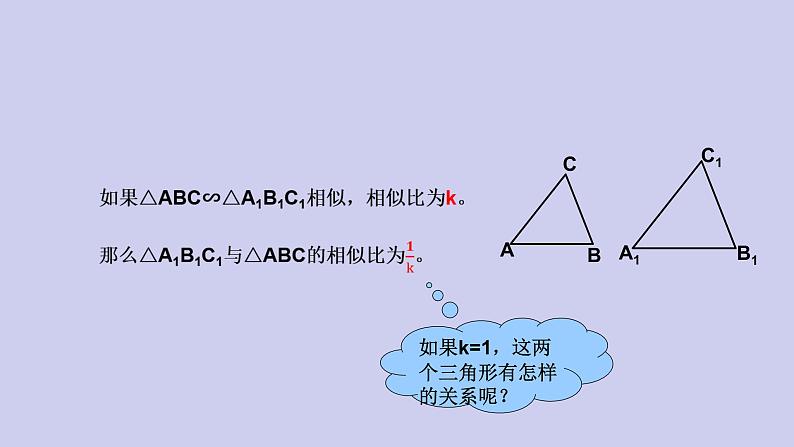
如果k=1,这两个三角形有怎样的关系呢?
判定两个三角形全等时,除了可以验证它们所有的角和边相等外,还可以使用简便的判定定理(SSS、SAS、ASA、AAS)。 类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
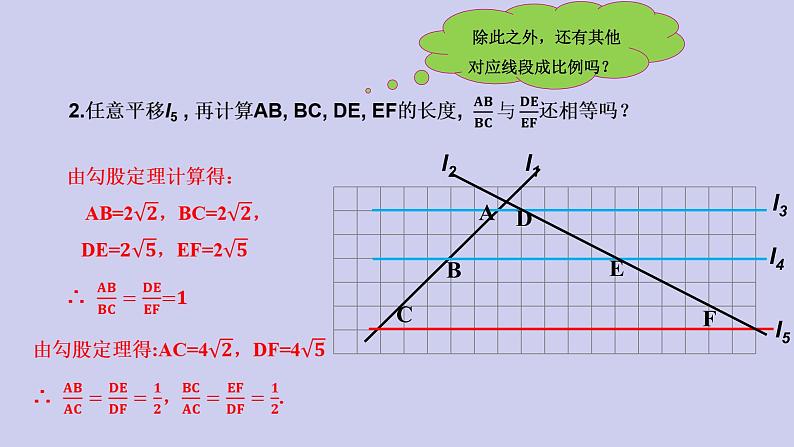
除此之外,还有其他对应线段成比例吗?
一般地,我们有平行线分线段成比例的基本事实: 两条直线被一组平行线所截,所得的对应线段成比例。
如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段。 如果把直线 l1向左或向右任意平移,这些线段依然成比例吗?
把直线l1 向左平移到D与A重合的位置,说一说图中有哪些成比例线段?如果把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
把直线l1 向左平移到E与B重合的位置,说一说图中有哪些成比例线段?如果把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
平行线分线段成比例定理的推论
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
【例2】如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E. △ADE与△ABC相似吗?
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E. 证明△ADE与△ABC相似.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
三角形相似的两种常见类型:
符号语言:∵ DE//BC,∴△ADE∽△ABC.
【例3】已知:如图,AB∥EF ∥CD,图中共有 对相似三角形。
△AOB∽△FOE
1.如图,△ABC∽△DEF,相似比为1:2,若 BC=1,则 EF 的长为( )A. 1 B. 2 C. 3 D. 4
3.如图,在△ABC中, EF∥BC. (1)如果E、F分别是 AB 和 AC 上的点, AE = BE=7, FC = 4 ,那么 AF 的长是多少?
3.如图,在△ABC中, EF∥BC. (2)如果AB = 10,AE=6,AF = 5,那么 FC 的长是多少?
初中数学人教版九年级下册27.2.1 相似三角形的判定课文内容课件ppt: 这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定课文内容课件ppt,共17页。PPT课件主要包含了相似多边形概念,相似多边形特征,相似比概念,相似多边形对应边的比,△ADE∽△ABC等内容,欢迎下载使用。
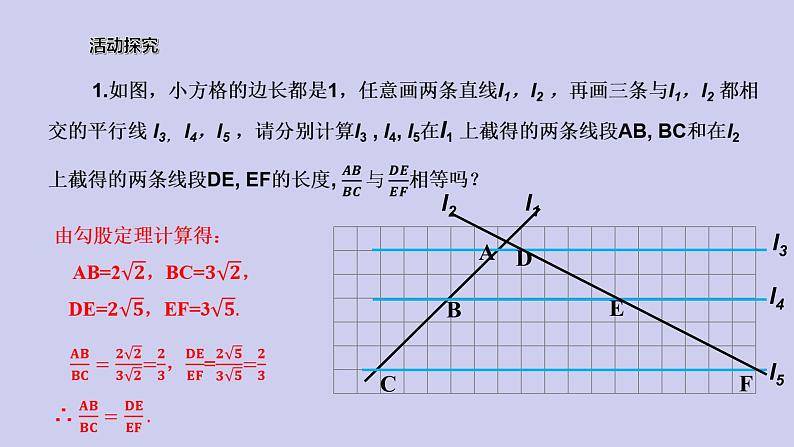
数学九年级下册27.2.1 相似三角形的判定评课ppt课件: 这是一份数学九年级下册27.2.1 相似三角形的判定评课ppt课件,共19页。PPT课件主要包含了由勾股定理得,∵∠A∠A等内容,欢迎下载使用。
初中数学人教版九年级下册27.2.1 相似三角形的判定备课课件ppt: 这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定备课课件ppt,共19页。PPT课件主要包含了新课准备,相似三角形,新课讲解,试一试,做一做,∵DE∥BC,∴BC12,课堂小结,随堂检测等内容,欢迎下载使用。













