2023年广东省清远市佛冈县二校联考一模数学试题

2023年广东省清远市佛冈县二校一模

数学试题

一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑。

1 .在Rt△ABC中,∠C=90°,sin A=,则tan B的值是 (　　)

A.         B.1         C.           D.

2 ．如图所示，已知AB∥CD，下列结论正确的是（　　）

   A．∠1=∠2 B．∠2=∠3 C．∠1=∠4 D．∠3=∠4 

3．2019年10月1日，天安门广场迎来新中国成立以来的第15次国庆阅兵．据统计，截止至当天下午6点，央视新闻置顶的“国庆阅兵”阅读数已超过34亿．数据34亿用科学记数法表示为（　　）

A．0.34×1010 B．3.4×109 C．3.4×108 D．34×108

4．已知x是整数，当||取最小值时，x的值是（　　）

A．5 B．6 C．7 D．8

5．函数y＝ax2+bx+c和y＝ax+b在同一坐标系中的图象大致是（　　）

A． B． 

C． D．

6．骰子：六个面上分别刻有1，2，3，4，5，6个小圆点的小正方体）一个质地均匀的正方形骰子的六个面分别刻有1至6的点数，将骰子抛掷两次，掷第一次，将朝上一面的点数记为x，掷第二次，将朝上一面的点数记为y，则点（x，y）落在直线y=﹣x+5上的概率为（　　）

   A． B． C． D． 

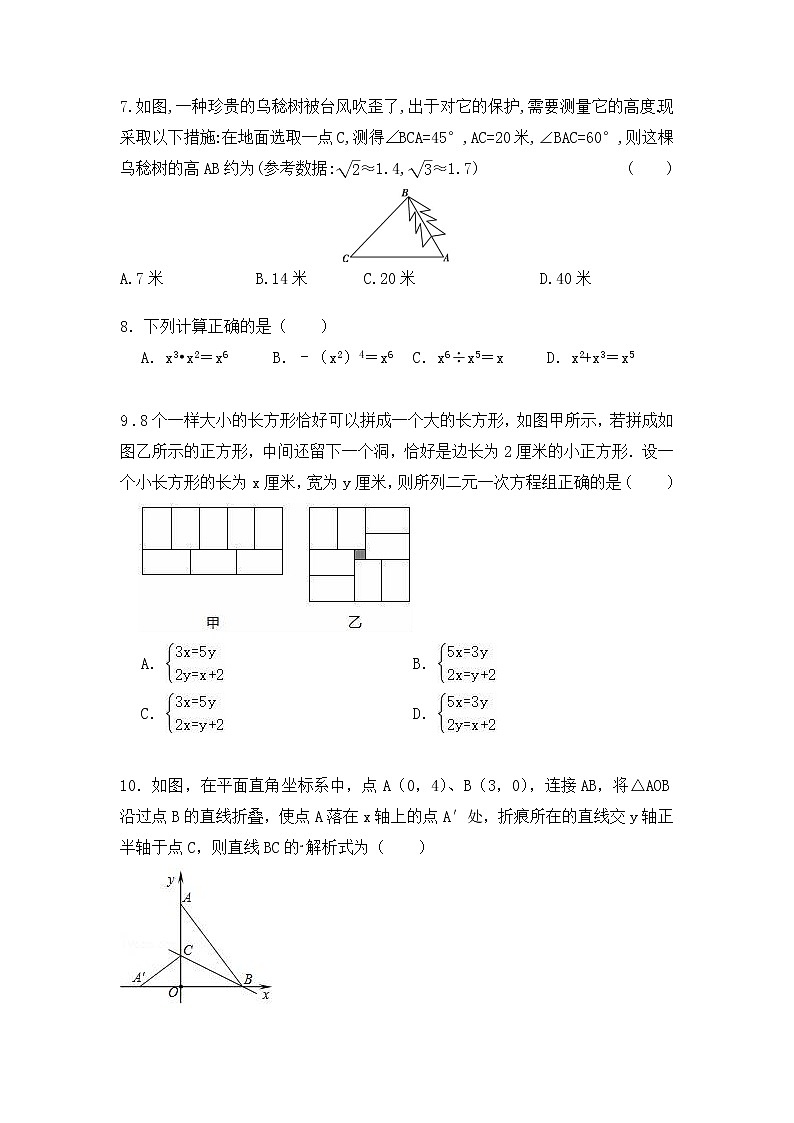
7.如图,一种珍贵的乌稔树被台风吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)              (　　)

A.7米           B.14米       C.20米               D.40米

8．下列计算正确的是（　　）

A．x3•x2＝x6 B．﹣（x2）4＝x6 C．x6÷x5＝x D．x2+x3＝x5

9 .8个一样大小的长方形恰好可以拼成一个大的长方形，如图甲所示，若拼成如图乙所示的正方形，中间还留下一个洞，恰好是边长为2厘米的小正方形．设一个小长方形的长为x厘米，宽为y厘米，则所列二元一次方程组正确的是（　　）

A． B． 

C． D．

10．如图，在平面直角坐标系中，点A（0，4）、B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为（　　）

A．y=﹣ B．y=﹣x+ C．y=﹣ D．y=﹣2x+

二、填空题（本大题5小题，每小题5分，共25分）请将下列各题的正确答案填写在答题卡的位置上．

11．已知扇形的弧长为4π，半径为8，则此扇形的圆心角为　   　度．

12．若关于x的方程有增根，实数m的值为 　   　．

13 .已知点A(x1,y1),B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1　　　　y2. 

14．已知实数a，b，在数轴上的对应点位置如图所示，则a+b﹣2　   　0（填“＞”“＜”或“＝”）．

15．如图，在△ABC中，BA＝BC，∠ABC＝90°，AC＝4，D为AC的中点，以D为圆心，DB为半径作圆心角为90°的扇形DEF，则图中阴影部分的面积为　   　．

三、计算题（本大题2小题，每小题6分，共12分)

16.(cos 30°+(3-π)0-2tan 45°

17. 若整数a使得关于x的分式方程有正整数解，且使得关于y的不等式组有解，那么符合条件的所有整数a的和是多少？

四、解答题（本大题4小题，共33分）

18.如图,在一次地震抢险救灾行动中,救援队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象.已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°.求该生命迹象C处与地面的距离.(结果精确到0.1米.参考数据:≈1.41,≈1.73)

19．如图，双曲线y=（x＞0）经过△OAB的顶点A和OB的中点C．AB∥x轴，点A的坐标为（4，6），连接AC交x轴于D．连接BD．

（1）确定k的值；

（2）求直线AC的解析式；

（3）判断四边形OABD的形状，并说明理由；

（4）求△OAC的面积．

20．为改善河流水质，某治污公司决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格与月处理污水量如表：

经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少5万元．

（1）求x、y的值；

（2）如果治污公司购买污水处理设备的资金不超过95万元，求该治污公司有哪几种购买方案；

（3）在（2）的条件下，如果月处理污水量不低于2040吨，为了节约资金，请为该公司设计一种最省钱的购买方案．

21.如图，在平面直角坐标系中，已知抛物线y＝ax2+4x+c与直线AB相交于点A（0，1）和点B（3，4）．

（1）求该抛物线的解析式；

（2）设C为直线AB上方的抛物线上一点，连接AC，BC，以AC，BC为邻边作平行四边形ACBP，求四边形ACBP面积的最大值；

（3）将该抛物线向左平移2个单位长度得到抛物线（a1≠0），平移后的抛物线与原抛物线相交于点D，是否存在点E使得△ADE是以AD为腰的等腰直角三角形？若存在，直接写出点E的坐标；若不存在，请说明理由．

答案

1.D

2.C

3.A

4.D．

6.C

7.B

8．C

9．A

10．C

11．90

　12．解：去分母，得2mx﹣（m+1）＝x+1，

∵关于x的方程有增根，

将增根为x＝﹣1代入2mx﹣（m+1）＝x+1，

得﹣2m﹣（m+1）＝0，

解得m＝﹣，

将增根为x＝0代入2mx﹣（m+1）＝x+1，

得﹣（m+1）＝1，

解得m＝﹣2，

∴m的值为﹣或﹣2，

故答案为：﹣或﹣2．

13. >

14．＜．

15．解：在Rt△ABC中，∠ABC＝90°，BC＝AB，AC＝4，

由勾股定理得：BC＝AB＝2，

∵在Rt△ABC中，∠ABC＝90°，BC＝AB，AC＝4，D为AC的中点，

∴BD＝AC＝2＝DE＝DF，CD＝AD＝2，∠DBM＝∠ABC＝45°＝∠A＝，CD＝AD，∠BDA＝90°，

∵∠MDN＝90°，

∴∠MDB＝∠NDA＝90°﹣∠BDN，

在△BDM和△ADN中，

，

∴△BDM≌△ADN（ASA），

∴△ADN与△BDN的面积之和＝△BDM与△BDN的面积之和，

∴四边形DNBM的面积等于△CDB的面积，

∴阴影部分的面积是S＝S扇形DEF﹣S四边形DNBM＝﹣××2×2＝π﹣2，

故答案为：π﹣2

16 .(1)cos 30°+(3-π)0-2tan 45°

=×+1-2

=+1-2

=.

17.解：解方程分式方程，

得x＝，

∵分式方程的解为正整数解，

∴a﹣2＝1或2或4或8，

又x≠4且x≠0，

∴a≠4，

∴a＝3或6或10，

∵关于y的不等式组有解，

∴2a﹣5＞1，

解得：a＞3，

综上，符合题意的整数a的值有6，10，

∴符合条件的所有整数a的和为16．

　18   .如图,过点C作CD⊥AB于点D,

设CD=x米,依题意,得∠CAD=30°,∠CBD=60°.

在Rt△ACD中,tan∠CAD==,∴AD=x米,

在Rt△BCD中,tan∠CBD==,∴BD=x米,

∵AB=AD-BD=x-x=4(米),

∴x=2≈3.5,

∴生命迹象C处与地面的距离约为3.5米.

19．解：（1）将A（4，6）代入解析式y=得：k=24；

（2）∵AB∥x轴，B的纵坐标是6，C为OB中点，

∴把y=3代入反比例解析式得：x=8，即C坐标为（8，3），

设直线AC的解析式为y=kx+b，

将A（4，6）与C（8，3）代入得：，

解得：，

则直线AC解析式为y=﹣x+9；

（3）四边形OABC为平行四边形，理由为：

∵点C的坐标为（8，3），

∴B的坐标为（16，6），即AB=12，

把y=0代入y=﹣x+9中得：x=12，即D（12，0），

∴OD=12，

∴AB=OD，

∵AB∥OD，

∴四边形OABC为平行四边形；

（4）∵S四边形OABC=12×6=72，

∴S△OAC=S四边形OABC=18．

20．解：（1）由题意，得，

解得，

（2）设治污公司决定购买A型设备a台，则购买B型设备（10﹣a）台，

由题意，得 11a+9（10﹣a）≤95，

解得，

∴0≤a≤，

∵a为整数，

∴a＝0或1或2，

∴，该公司有以下三种方案：

方案一：A型设备0台，B型设备为10台；

方案二：A型设备1台，B型设备为9台；

方案三：A型设备2台，B型设备为8台；

（3）由题意，得 240a+200（10﹣a）≥2040，

解得：a≥1，

∴a＝1或2，

当a＝1时，买设备所需资金为：11+9×9＝92万元；当a＝2时，买设备所需资金为：11×2+9×8＝94万元；

∴按方案二：购买A型设备1台，B型设备9台最省钱．

21 解：（1）将A、B两点代入到解析式中，得，

，

解得，

∴抛物线的解析式为：y＝﹣x2+4x+1；

（2）设直线AB为：y＝k1x+1，

代入点B，得，3k1+1＝4，

解得k1＝1，

∴直线AB为：y＝x+1，

设C（m，﹣m2+4m+1），过C作CM∥y轴交AB于M，如图，

则M（m，m+1），

∴CM＝﹣m2+4m+1﹣m﹣1＝﹣m2+3m，

∵四边形ACBP为平行四边形，

∴S四边形ACBP＝2S△ABC＝2（S△ACM+S△BCM）＝2×CM×3＝4CM＝3（﹣m2+3m）＝﹣3（m﹣）2+，

∵﹣3＜0，

∴m＝时，四边形ACBP面积的最大值为；

（3）∵抛物线y＝﹣x2+4x+1＝﹣（x﹣2）2+5，

∴将抛物线向左平移2个单位后得到的抛物线为：y＝﹣x2+5，

联立，解得，

∴D（1，4），

①如图，当DA＝DE，∠EDA＝90°，E在AD右侧时，过D作x轴平行线交y轴于N，过E作y轴平行线，两线交于F点，

∵∠DAN+∠NDA＝∠NDA+∠EDF＝90

∴∠DAN＝∠EDF