福建省厦门市同安区2022-2023学年七年级上学期期末考试数学试卷(含解析)

2022-2023学年第一学期七年级期末质量检测

数学

一、选择题（本大题共10小题，每小题4分，共40分．每小题都有四个选项，其中有且只有一个选项符合题目要求．）

1. 的相反数是（    ）

A.  B.  

C.  D.

2. 如图是某几何体的展开图，该几何体是（    ）

A. 长方体 B. 正方体 C. 圆锥 D. 圆柱

3. 2022年6月5日，神舟十四号载人飞船成功点火升空．神舟十四号载人飞船的“问天实验舱”舱体总长17.9米，直径4.2米，重量约，是我国目前最重、尺寸最大的单体飞行器．23000这个数字用科学记数法表示为（    ）

A.  B.  

C.  D.

4. 下列选项中的两个整式是同类项的是（    ）

A. 和 B. 和 C. 和 D. 和

5. 有理数a，b在数轴上的对应点的位置如图所示，下列结论正确的是（    ）

A.  B.  C.  D.

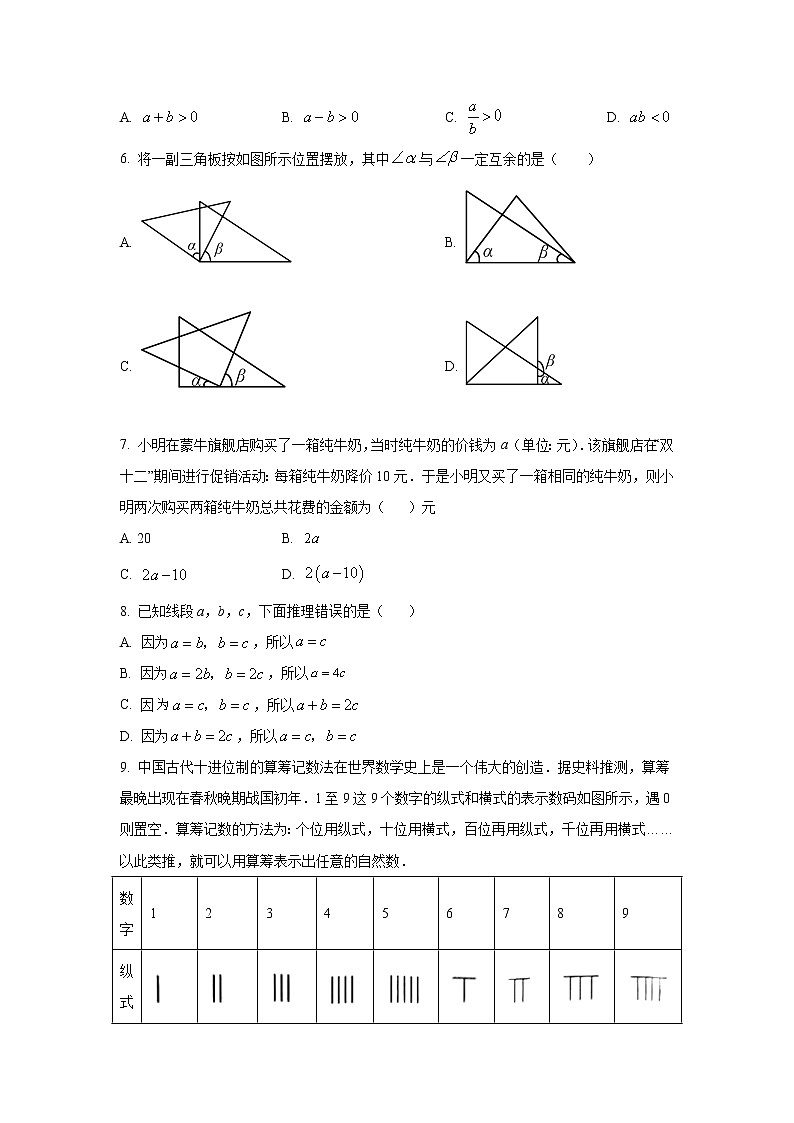
6. 将一副三角板按如图所示位置摆放，其中与一定互余的是（    ）

A.  B.

C.  D.

7. 小明在蒙牛旗舰店购买了一箱纯牛奶，当时纯牛奶的价钱为a（单位：元）．该旗舰店在“双十二”期间进行促销活动：每箱纯牛奶降价10元．于是小明又买了一箱相同的纯牛奶，则小明两次购买两箱纯牛奶总共花费的金额为（    ）元

A. 20 B.  

C.  D.

8. 已知线段a，b，c，下面推理错误的是（    ）

A. 因为，所以 

B. 因为，所以

C. 因，所以 

D. 因为，所以

9. 中国古代十进位制的算筹记数法在世界数学史上是一个伟大的创造．据史料推测，算筹最晚出现在春秋晚期战国初年．1至9这9个数字的纵式和横式的表示数码如图所示，遇0则置空．算筹记数的方法为：个位用纵式，十位用横式，百位再用纵式，千位再用横式……以此类推，就可以用算筹表示出任意的自然数．

根据上述材料，为的运算结果可用算筹表示为（    ）

A.  B.  

C.  D.

10. 已知数轴上点A，B表示的数分别为和30，现有一动点P以2个单位每秒的速度从点A出发，沿数轴正方向运动，当时，运动的时间为（    ）

A. 10秒 B. 15秒 C. 15秒或25秒 D. 15秒或30秒

二、填空题（本大题有6小题，第11小题12分，其余每小题4分，共32分）

11. 计算：（1）_________；（2）__________；（3）_________；（4）_________；（5）__________；（6）_________．

12. 与原点距离为3的点表示的数是____________．

13. ________________'．

14. 已知关于x的方程的解是，则m的值为__________．

15. 已知，从点O引一条射线，使得，则_______．

16. 如图，，点C是线段延长线上的动点，在线段上取一点N，使得，点M为线段的中点，则___________．

三、解答题（本大题有9小题，共78分）

17. 计算：

（1）

（2）

18 解方程：

（1）

（2）

19 先化简，再求值：，其中．

20. 如图，已知点B在线段上．

（1）尺规作图：在线段上作一点D，使得（不写过程，保留作图痕迹）；

（2）在（1）的条件下，，， E为中点，求线段的长．

21. 如图，点O在直线上，，，是的角平分线，求的度数．

22. 甲、乙两车从相距的两地同时出发相向而行，甲车的速度比乙车的速度快，2小时后两车相遇．求甲、乙两车的速度．（请你用一元一次方程的知识解决问题）

23. 定义：对于一个三位正整数，如果十位数字恰好等于百位数字与个位数字之和的一半，我们称这个三位正整数为“半和数”．

例如，三位正整数234，因为，所以234是“半和数”．

（1）判断147是否为“半和数”，并说明理由；

（2）小林列举了几个“半和数”：111、123、234、840…，并且她发现：，，，…，所以她猜测任意一个“半和数”都能被3整除．小林的猜想正确吗？若正确，请你帮小林说明该猜想的正确性；若不正确，说明理由．

24. 如图，已知与互补．

（1）若，求的度数；

（2）若为的角平分线，射线在的内部，射线在的内部，且满足，探究与之间有什么样的数量关系，请写出结论，并说明理由．

25. 杨先生准备购买一套小户型商品房，他在了解A、B两楼盘的过程中，均有钟意的商品房．

从A楼盘获取的信息

①购房单价为3万元/；

②购房优惠方案为：可免费赠送书房面积（注：赠送面积不需要付钱）；

③杨先生钟意A楼盘商品房平面图如下图所示：

从B楼盘获取的信息

①购房单价为3万元/；

②购房优惠方案如下；

③杨先生在B楼盘钟意的一套商品房，享受优惠后的价格为214万元．

（1）根据A楼盘商品房平面图，过道的长度为_________m（用含有x的式子表示）；

（2）若A楼盘杨先生钟意商品房总面积为，请求出书房宽x的值，并计算若杨先生购买该商品房，应付多少钱？

（3）在（2）的基础上杨先生打算从A、B楼盘里选择每平方米实付单价最低的商品房（每平方米实付单价单位：元/），请你帮杨先生算一算，他应该选择哪个楼盘所钟意的商品房？（结果保留3位小数）

答案

1. B

解：根据相反数定义，的相反数是，

故选：B．

2. C

解：∵展开图由一个扇形和一个圆构成，

∴该几何体是圆锥．

故选C．

3. B

解：．

故选：B．

4. A

解：A、和是同类项，故选项符合题意；

B、和所含字母不相同，不是同类项，故选项不符合题意；

C、和相同字母的指数不相同，不是同类项，故选项符合题意；

D、和相同字母的指数不相同，不是同类项，故选项不符合题意．

故选：A．

5. D

解：由数轴可知，且，

∴，故选项A错误，不符合题意；

，故选项B错误，不符合题意；

，故选项C错误，不符合题意；

，故D正确，符合题意．

故选：D．

6. C

解：A．两角不一定互余，选项错误，不符合题意；

B．=45°，=30°，两角不互余，选项错误，不符合题意；

C．+=180°-90°=90°，两角互余，选项正确，符合题意；

D．+=180°，两角互补，选项错误，不符合题意；

故选：C．

7. C

解：根据题意得，

则小明两次购买两箱纯牛奶总共花费的金额为元，

故选：C．

8. D

解：A、因为，所以（等量代换），故原推理正确；

B、因为，所以，故原推理正确；

C、因为，所以，故原推理正确；

D、因为，所以a，b，c之间不一定相等，故原推理不正确．

故选：D．

9. C

解：，

根据计算法则：百位是2用纵式，十位是1用横式，个位是6用纵式，由表格中各个数字的横式、纵式所对应的符号可得，

故选：C．

10. D

解：当时，设运动的时间为x，

则点P表示的数为，，

由题意得，

即或，

解得或，

即：运动的时间为15秒或30秒时．

故选：D．

11. ①. 9    ②. 0    ③.     ④.     ⑤.     ⑥. 3

解：（1）；

（2）；

（3）；

（4）；

（5）；

（6）．

故答案为：（1）9；（2）0；（3）；（4）；（5）；（6）3．

12.

解：根据题意,该点离原点的距离是3个单位长度，

设这点表示的数为a

即 |a| = 3，

进而可得，a =

故答案为：．

13. ① 20    ②. 30

解：∵，

∴，

∴．

故答案为：20；30．

14. 8

解：将代入方程可得：

，

∴，

故答案为：8．

15. 或

解：当在内部时，

，

又，

∴；

当在外部时，

，

又，

∴；

故答案为：或．

16. 5

解：设，则，

∴，

∵点M为线段的中点，

∴，

∴，

∴．

故答案为：5．

17. （1）

解：

；

（2）

解：

．

18. （1）

解：，

移项，得，

合并同类项，得，

系数化为1，得；

（2）

解：，

去分母，得，

去括号，得，

移项，得，

合并同类项，得，

系数化为1，得．

19. 解：

，

当时，原式．

20. （1）

解：如图，

，

点D即为所求；

（2）

解：∵， ，

∴，

又，

∴，

∵E为中点，

∴，

∴．

21. 解：∵，，

∴，

又是的角平分线，

∴，

∴．

22. 解：设乙车的速度是，则甲车的速度是，

根据题意，得，

解得，

∴，

答：甲车的速度是，乙车的速度是．

23. （1）

解：∵的百位数字为1，十位数字为4，个位数字为7，且，

∴是“半和数”；

（2）

解：小林的猜想正确．

理由：设一个“半和数”的百位数字为m，个位数字为n（m，n均为整数，且m不为0），

则这个“半和数”用含m，n的代数式表示为：

，

∵m，n均为整数，

∴为整数，

∴是3的倍数，

∴任意一个“半和数”都能被3整除．

故小林的猜想正确．

24. （1）

解：∵与互补，，

∴；

（2）

解：．理由如下，

设，，

∴，，

∵为的角平分线，

∴，

∴，即，

，

∴．

25. （1）

解：由题意，得：过道长为m,

故答案为：；

（2）

解：根据题意，得，

解得，

∴杨先生购买该商品房，应付（万元），

答：书房宽为1.8米，杨先生购买该商品房，应付197.4万元；

（3）

解：∵，，

∴杨先生在B楼盘钟意的一套商品房原价超过200万元，不足300万元，

设杨先生在B楼盘钟意的一套商品房原价为m元，

则，

解得，

∴杨先生在B楼盘钟意的一套商品面积为，

∴B楼盘里每平方米实付单价为万元/，

又A楼盘里每平方米实付单价万元/，

∴他应该选择B楼盘所钟意的商品房．