初中数学北京课改版九年级上册第十九章二次函数和反比例函数19.5 反比例函数优质ppt课件

展开

这是一份初中数学北京课改版九年级上册第十九章二次函数和反比例函数19.5 反比例函数优质ppt课件，共22页。PPT课件主要包含了一条直线，一条抛物线，探究归纳，课内检测，拓展提升等内容，欢迎下载使用。

1.我们知道一次函数y＝kx＋b（k≠0）的图象是、二次函数的图象是，反比例函数的图象是什么样呢？2.我们用什么方法画反比例函数的图象呢？有哪些步骤？3.根据k的取值，应该如何分类讨论呢？
y＝ax2 ＋bx＋c（a≠0）
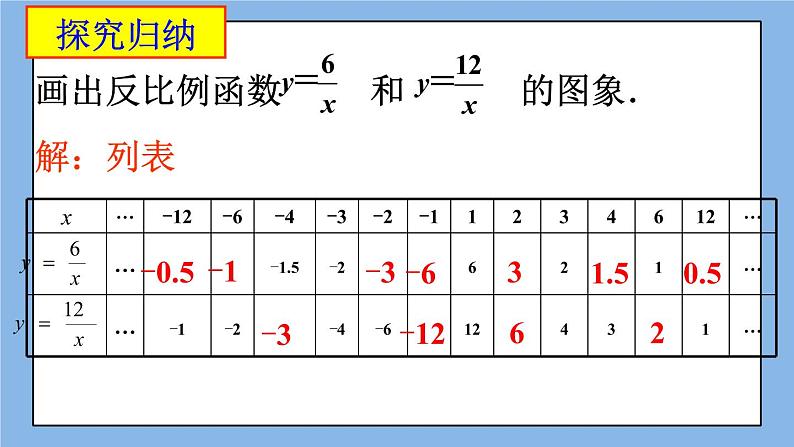
画出反比例函数和的图象．
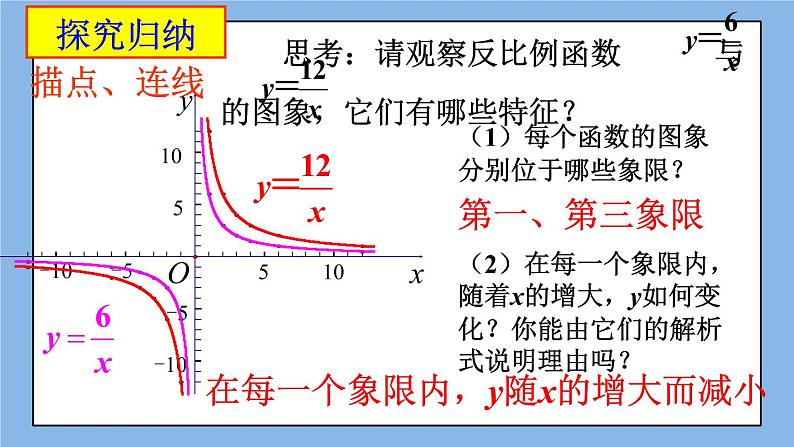
思考：请观察反比例函数与的图象，它们有哪些特征？
（1）每个函数的图象分别位于哪些象限？（2）在每一个象限内，随着x的增大，y如何变化？你能由它们的解析式说明理由吗？
在每一个象限内，y随x的增大而减小
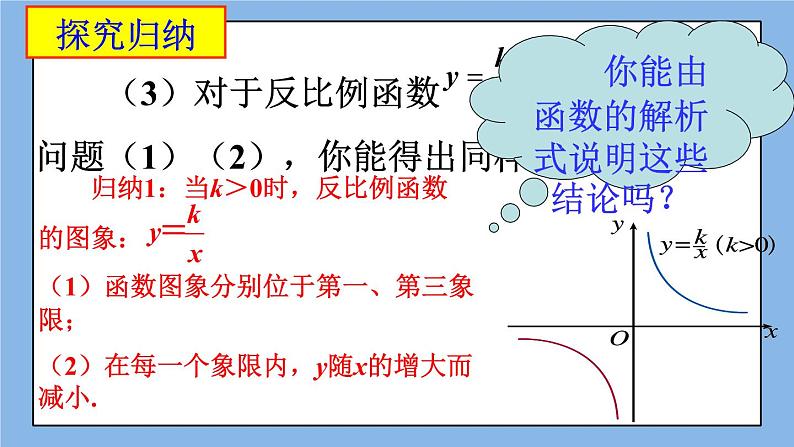
（3）对于反比例函数，考虑问题（1）（2），你能得出同样的结论吗？
归纳1：当k＞0时，反比例函数的图象：（1）函数图象分别位于第一、第三象限；（2）在每一个象限内，y随x的增大而减小.
你能由函数的解析式说明这些结论吗？
探究：回顾上面我们利用函数图象，从特殊到一般研究反比例的性质的过程，你能用类似的方法研究反比例的图象和性质吗？
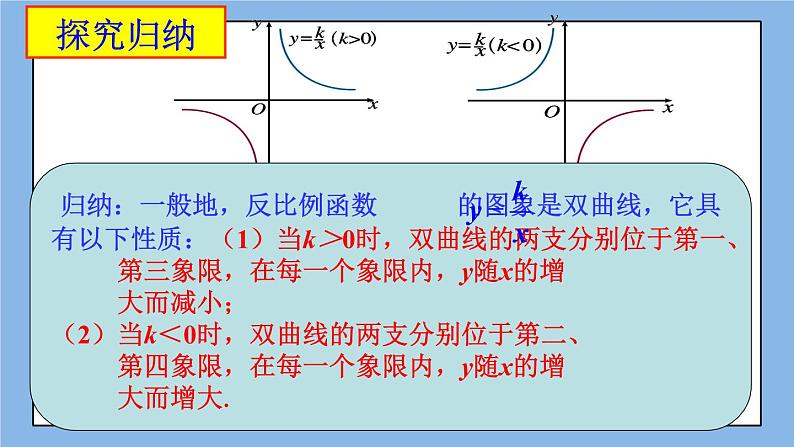
归纳2：当k＜ 0时，反比例函数的图象：（1）函数图象分别位于第二、第四象限；（2）在每一个象限内，y随x的增大而增大.
反比例函数的图象由两条曲线组成，它是双曲线.
归纳：一般地，反比例函数的图象是双曲线，它具有以下性质：（1）当k＞0时，双曲线的两支分别位于第一、第三象限，在每一个象限内，y随x的增大而减小；（2）当k＜0时，双曲线的两支分别位于第二、第四象限，在每一个象限内，y随x的增大而增大.
可得k=12，函数的表达式为
例2 某厂计划建造一个容积为4×104m3的长方体蓄水池．（1）蓄水池的底而积S（m2）与其深度h（m）有怎样的函数关系？（2）如果蓄水池的深度设计为5m，那么它的底面积应为多少？（3）如果考虑绿化以及辅助用地的需要，蓄水池的长和宽最多只能分别设计为100m和60m，那么它的深度至少应为多少米（精确到0.01）?
（3）根据题意，得 S=100×60=6000.
1．如图所示的图象对应的函数解析式（）. A． B． C． D．
2．反比例函数的图象在第象限．
3．已知一个反比例函数的图象经过点 A（3，－4）．（1）这个函数的图象位于哪些象限？在图象的每一支上，y 随 x 的增大如何变化？（2）点B（－3，4），C（－2，6），D（3，4）是否在这个函数的图象上，为什么？
解：（1）∵由题可知，函数解析式为
∴函数图象位于第二、第四象限. 在图象的每一支上， y 随 x 的增大而增大.
（2）点B、C在这个函数的图象上，它们的坐标满足这个函数解析式；点D不在这个函数的图象上，它的坐标不满足这个函数解析式；
1．下列图象中是反比例函数图象的是（　）
2．已知反比例函数的图象如图所示，则k 0，且在图象的每一支上，y 随 x 的增大而．
3．已知反比例函数的图象过点（2，1），则它的图象在___________象限，k____0．
4．点 A（x1，y1）和点 B（x2，y2）在反比例函数的图象上．如果x1＜x2，而且x1，x2同号，那么y1，y2有怎样的大小关系？为什么？
∵反比例函数的图象位于第一、第三象限，∴在每一个象限内，y随x的增大而减小.
2．点 A（x1，y1）和点 B（x2，y2）在反比例函数的图象上，如果x1＞0＞x2，那么 y1 和 y2 有怎样的关系？
解：有两种情况，（1）当k＞0时， y1 ＞ y2 ；（2）当k＜0时， y1 ＜ y2 .
码头工人以每天30吨的速度往一艘轮船上装载货物，把轮船装载完毕恰好用了8天时间. (1)轮船到达目的地后开始卸货，卸货速度v（单位：吨／天）与卸货时间t（单位：天）之间有怎样的函数关系？
(2)由于遇到紧急情况，船上的货物必须在不超过5日内卸载完毕，那么平均每天至少要卸多少吨货物？
分析:根据装货速度×装货时间=货物的总量，可以求出轮船装载货物的总量；再根据卸货速度=货物的总量÷卸货时间，得到v与t的函数关系式.
在同一直角坐标系中，函数与的图象大致是（）． A.（1）（2）B. （1）（3） C. （2）（4） D. （3）（4）