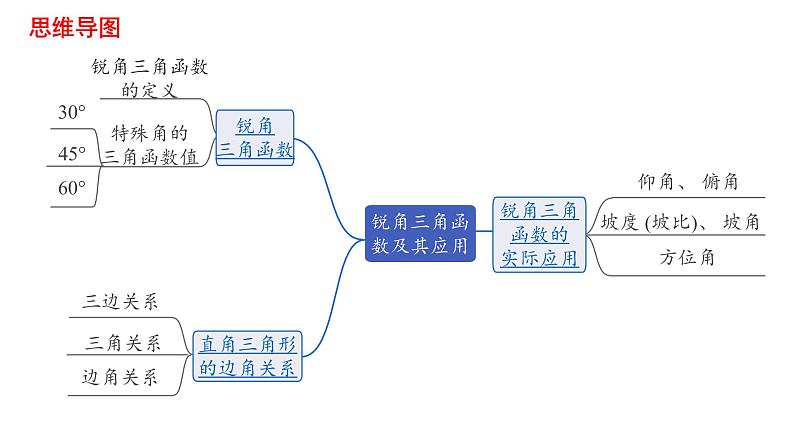
2023年中考数学一轮复习课件： 锐角三角函数及其应用

这是一份2023年中考数学一轮复习课件： 锐角三角函数及其应用，共26页。PPT课件主要包含了锐角三角函数及其应用，思维导图，考点梳理，sinB，第1题图，随堂练习，第2题图，第3题图，第4题图，第5题图等内容，欢迎下载使用。

考点1 锐角三角函数
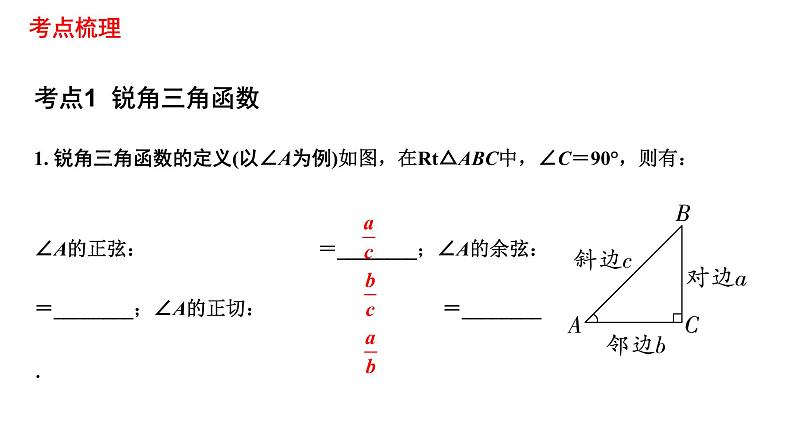
1. 锐角三角函数的定义(以∠A为例)如图，在Rt△ABC中，∠C＝90°，则有：
∠A的正弦： ＝________；∠A的余弦： ＝________；∠A的正切： ＝________．
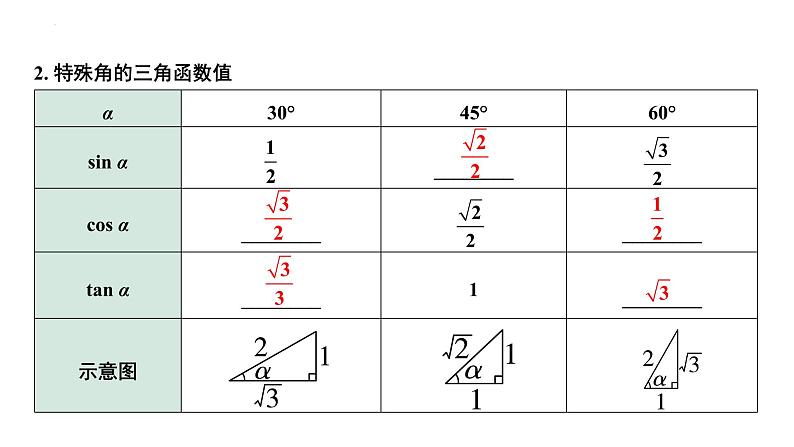
2. 特殊角的三角函数值
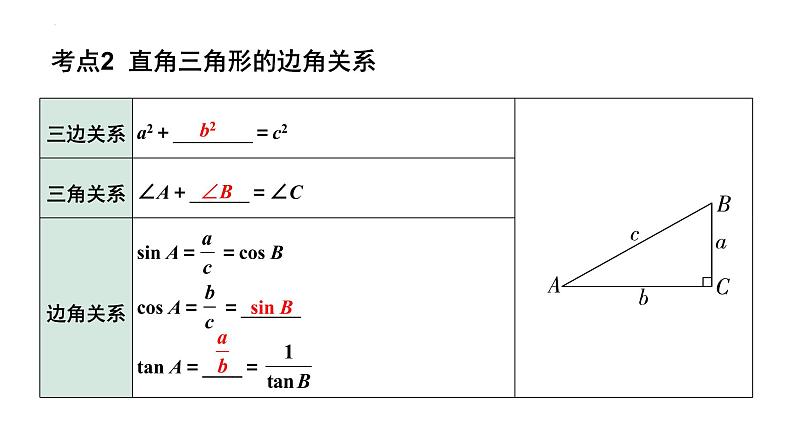
考点2 直角三角形的边角关系
考点3 锐角三角函数的实际应用
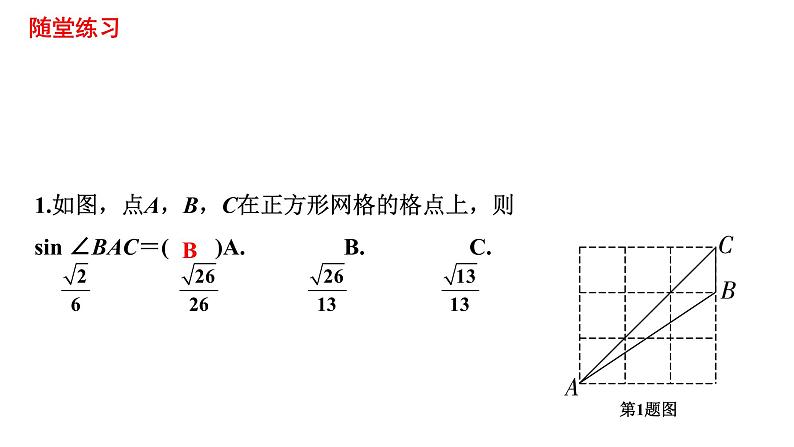
1.如图，点A，B，C在正方形网格的格点上，则sin ∠BAC＝(　　)A. B. C. D.
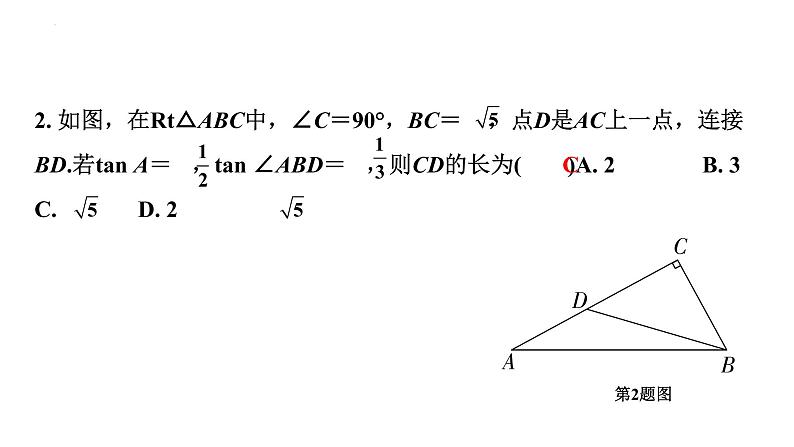
2. 如图，在Rt△ABC中，∠C＝90°，BC＝ ，点D是AC上一点，连接BD.若tan A＝ ，tan ∠ABD＝ ，则CD的长为(　　)A. 2 B. 3 C. D. 2
3.如图所示，△ABC的顶点在正方形网格的格点上，则tan A的值为(　　)A. B. C. 2 D. 2
4. 如图，在Rt△ABC中，∠B＝90°，AB＝5，BC＝12，将△ABC绕点A逆时针旋转得到△ADE，使得点D落在AC上，则 tan ∠ECD的值为________．
5. 如图，AB和CD两幢楼地面距离BC为30 米，楼AB高30米，从楼AB的顶部点A测得楼CD的顶部点D的仰角为45°.(1)求∠CAD的大小；
解：(1)如图，过点A作AH⊥CD于点H，
∴∠HAC＝30°.∵∠DAH＝45°，∴∠CAD＝75°；
(2)求楼CD的高度(结果保留根号).
6. 如图，海中有两小岛C，D，某渔船在海中的A处测得小岛C位于东北方向，小岛D位于南偏东30°方向，且A，D相距10 n mile.该渔船自西向东航行一段时间后到达点B，此时测得小岛C位于西北方向且与点B相距8 n mile.求B，D间的距离(计算过程中的数据不取近似值).
如图，过点D作DM⊥AB，垂足为M，则∠ADM＝30°.
7.宜宾东楼始建于唐代，重建于宜宾建城2200周年之际的2018年，新建成的东楼(如图①)成为长江首城会客厅、旅游休闲目的地、文化地标打卡地．某数学小组为测量东楼的高度，在梯步A处(如图②)测得楼顶D的仰角为45°，沿坡比为7∶24的斜坡AB前行25米到达平台B处，测得楼顶D的仰角为60°，求东楼的高度DE.(结果精确到1米，参考数据： ≈1.7， ≈1.4)
解：∵在Rt△ABF中，坡比为7∶24，AB＝25，∴设BF＝7a，AF＝24a，∴(7a)2＋(24a)2＝252，解得a＝1，∴BF＝7，AF＝24，∵∠DAC＝45°，DC⊥AC，∴AC＝DC，∴BE＝CF＝AC－AF＝AC－24， DE＝DC－CE＝AC－BF＝AC－7，
∵∠DBE＝60°，∴tan 60°＝ ，解得AC＝ ≈47，∴DC＝47－7＝40(米)，答：东楼的高度DE约为40米．
8. 某数学兴趣小组自制测角仪到公园进行实地测量，活动过程如下：(1)探究原理制作测角仪时，将细线一端固定在量角器圆心 O处，另一端系小重物G.测量时，使支杆 OM，量角器 90°刻度线 ON与铅垂线 OG相互重合(如图①)，绕点 O转动量角器，使观测目标 P与直径两端点A，B共线(如图②)，此时目标P的仰角∠POC＝∠GON.请说明这两个角相等的理由．
(1)证明：∵∠POC＋∠CON＝∠CON＋∠GON＝90°，∴∠POC＝∠GON；
(2)实地测量如图③，公园广场上有一棵树，为测树高，同学们在观测点K处测得树顶端P的仰角∠POQ＝60°，观测点与树的距离KH为5米，点O到地面的距离OK为1.5米，求树高PH.( ≈1.73，结果精确到0.1米)
(3)拓展探究公园高台上有一凉亭，为测量凉亭顶端P距地面的高度PH(如图④)，同学们经过讨论，决定先在水平地面上选取观测点E，F(E，F，H在同一直线上)，分别测得点P的仰角α，β，再测得E，F间的距离m，点O1，O2到地面的距离O1E，O2F均为1.5米．求PH(用α，β，m表示).
得DO1＝ ，在Rt△PO2D中，tan β＝ ，得DO2＝ ，∵DO2＝O1O2＋DO1，∴DO1＝ －O1O2＝ ，∴PD＝＝ ，
∴PH＝PD＋DH＝( ＋1.5) 米．
9. 在一次数学课外实践活动中，小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°，从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°，综合楼高24米．请你帮小明求出办公楼的高度．(结果精确到0.1米，参考数据：tan 37°≈0.75，tan 53°≈1.33， ≈1.73)
解：在△ABD中，∠BAD＝90°，AB＝24，∠ABD＝90°－53°＝37°，