锐角三角函数中考复习课件-中考数学复习

这是一份锐角三角函数中考复习课件-中考数学复习，共29页。PPT课件主要包含了锐角三角数的定义，过手练，三边关系，三角关系，边角关系，仰角和俯角，方向角，坡度和坡角，中考真题，牛刀小试等内容，欢迎下载使用。

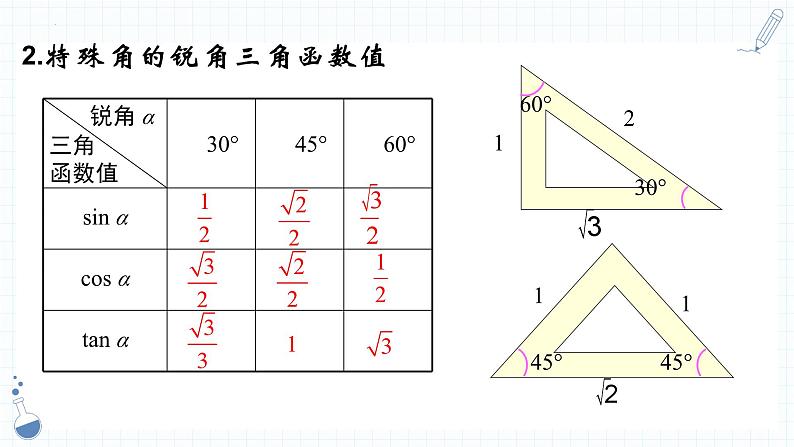
2.特殊角的锐角三角函数值
1.在Rt△ABC中，∠C=90°，AB=5,BC=4,那么下列各式中不正确的是（ ）
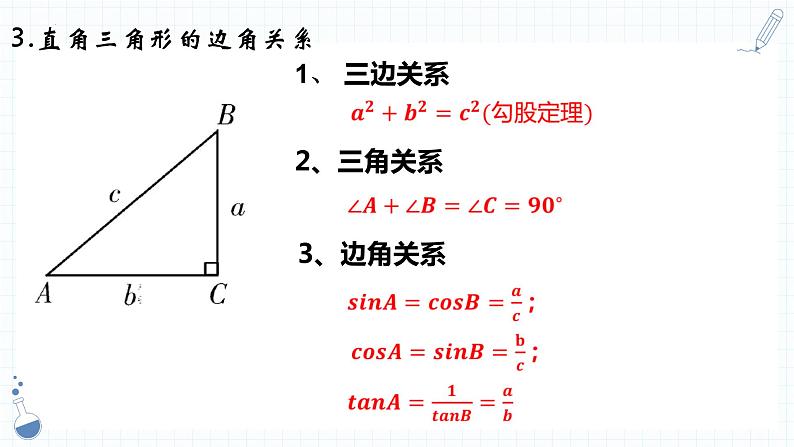
3.直角三角形的边角关系
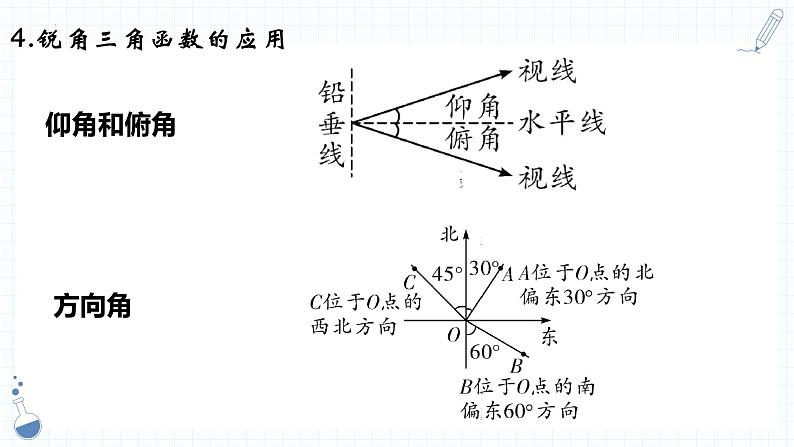
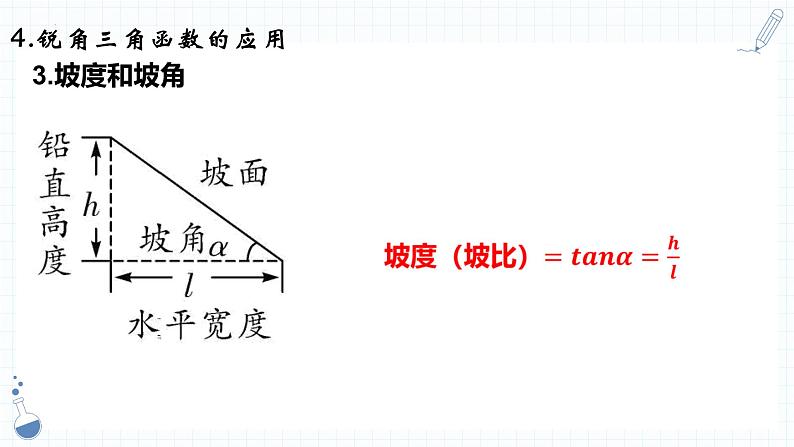
4.锐角三角函数的应用
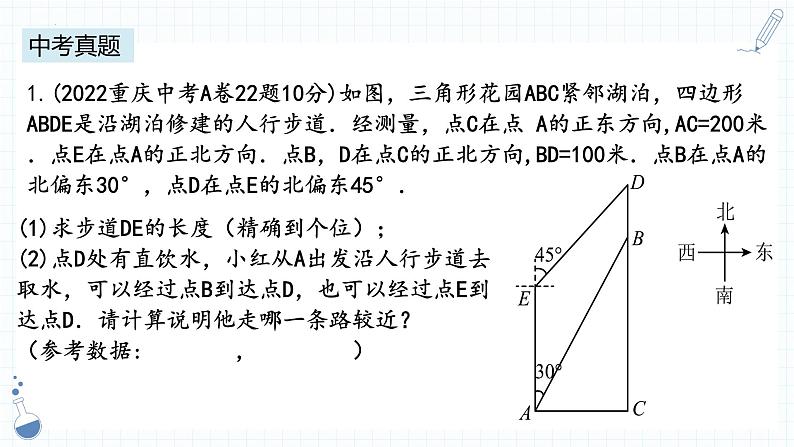
1.(2022重庆中考A卷22题10分)如图，三角形花园ABC紧邻湖泊，四边形ABDE是沿湖泊修建的人行步道．经测量，点C在点 A的正东方向,AC=200米．点E在点A的正北方向．点B，D在点C的正北方向,BD=100米．点B在点A的北偏东30°，点D在点E的北偏东45°．
(1)求步道DE的长度（精确到个位）；(2)点D处有直饮水，小红从A出发沿人行步道去取水，可以经过点B到达点D，也可以经过点E到达点D．请计算说明他走哪一条路较近？（参考数据: , ）
(1)求步道DE的长度（精确到个位）；（参考数据: , ）
解：过点E作BC的垂线，垂足为H,∴∠CAE=∠C=∠CHE=90°，∴四边形ACHE是矩形，∴EH=AC=200m，根据题意得：∠D=45°，∴△DEH为等腰直角三角形，∴DH=EH=200m，∴ （m）； <
(2)点D处有直饮水，小红从A出发沿人行步道去取水，可以经过点B到达点D，也可以经过点E到达点D．请计算说明他走哪一条路较近？
2.(2022重庆中考B卷22题10分)湖中小岛上码头C处一名游客突发疾病，需要救援．位于湖面B点处的快艇和湖岸A处的救援船接到通知后立刻同时出发前往救援．计划由快艇赶到码头C接该游客，再沿CA方向行驶，与救援船相遇后将该游客转运到救援船上．已知C在A的北偏东30°方向上，B在A的北偏东60°方向上，且B在C的正南方向900米处．
(1)求湖岸A与码头C的距离（结果精确到1米，参考数据： ）；(2)救援船的平均速度为150米/分，快艇的平均速度为400米/分，在接到通知后，快艇能否在5分钟内将该游客送上救援船？请说明理由．（接送游客上下船的时间忽略不计）
（1）求湖岸A与码头C的距离（结果精确到1米，参考数据： ）；
解：过点A作CB垂线，交CB延长线于点D，由题意可得：∠NAB=60°，∠NAC=30°，CB=900m，则∠CAD=60°，∠BAD=30°设BD=x,则AB=2x,AD= ,CD=900+x在Rt△ACD中， ，∴ ，解得x=450，在Rt△ACD中， ，
（2）救援船的平均速度为150米/分，快艇的平均速度为400米/分，在接到通知后，快艇能否在5分钟内将该游客送上救援船？请说明理由．（接送游客上下船的时间忽略不计）
解：设快艇将游客送上救援船时间为t分钟，由题意可得：150 t +400 t =900+1559， t ≈4.47＜5∴在接到通知后，快艇能在5分钟内将该游客送上救援船．
1.小张是“科技协会”的一名会员，他设计了一款距离测量仪器，这款仪器的最大测量距离为34m，（测量距离为两点所连线段的长度）.为了测试这款仪器的性能，小张来到一座小山坡．从山脚A处开始，作为测量点，手持仪器沿斜坡AB向上走．已知AC⊥BC，AC＝19.2m，BC＝8m．
解：∵AC⊥BC，AC＝19.2m，BC＝8m．
（2）小张到达B后继续测试，先走一段水平路面BD，BD∥AC，长为2.8m，再沿另一斜坡DE向上走，直到G点，此时G，A两点之间达到最大测量距离34m，且斜坡DE的仰角为45°,请求出DG的长度．（结果保留一位小数，在整个测量过程中，小张所走的路线在同一平面内：√?≈1.41，√? ≈1.73）
解：作GH⊥AC交AC的延长线于点H，交BF于点M，连接AG，设DM=x， ∵∠GDF=45° ∴DM=DM=x，DG=√?x ∴GH=8+x∵DB=2.8 ∴AH=AC+BD+DM=19.2+2.8+x=22+x
2.从2019年底以来，新冠疫情一直困扰着我们 日常生活，今年为进一步加强疫情防控工作，某公司决定安装红外线体温检测仪，这种设备的原理是采用非接触式测温法，只要用红外体温测试仪的镜头对准被测对象进行扫描，其体温就可立刻在显示屏上显示出来，从而有效地避免了其他常规测温法所可能造成的交叉感染，测温区域示意图如图所示，已知最大探测角∠PAO＝75°，最小探测角∠PBO＝30°（参考数据： ， ， ）
(1)若该设备安装在离水平地面距离为2.2m的P处，即OP＝2.2m，请求出图中OB的长度；（结果精确到0.1m）(2)若该公司要求测温区域AB的长度为4 m，请求出该设备的安装高度OP的高度．（结果精确到0.1 m）
（1）若该设备安装在离水平地面距离为2.2m的P处，即OP＝2.2m，请求出图中OB的长度；（结果精确到0.1m）
解：在Rt△OBP中， ∴ ， ∴ （m） 答：OB的长度为3.8米；
(2)若该公司要求测温区域AB的长度为4 m，请求出该设备的安装高度OP的高度．（结果精确到0.1 m）
(1)求点A到BE的距离． (2)DE段扶梯长度约为多少米？（结果保留1位小数）
(1)求点A到BE的距离．
解：作AH⊥EB于H，∵扶梯AB的坡度为3∶2，∴设 ，∵ , ∴ ，即 ，∴解得 （舍去），∴ 米，∴点A到BE的距离为30米；
(2)DE段扶梯长度约为多少米？（结果保留1位小数）
解：延长DG交AH于N，作DG⊥EB于G,∵∠ACD=135° ∴ ∠ACN=45° 在Rt△ACN中，AC=20 ，∠ACN=45° ∴ ∵AH=30∴ ∵四边形DGHN是矩形∴
4.如图，海上有一座小岛C，一艘渔船在海中自西向东航行，速度为60海里/小时，船在A处测得小岛C在北偏东45°方向，1小时后渔船到达B处，测得小岛C在北偏东30°方向（参考数据： ）
(1)求BC的距离；（结果保留整数）(2) 渔船在B处改变航行线路，沿北偏东75°方向继续航行，此航行路线记为l，但此时发现剩余油量不足，于是当渔船航行到l上与小岛C最近的D处时，立即沿DC方向前往小岛C加油，加油时间为18分钟，在小岛C加油后，再沿南偏东75°方向航行至l上的点E处．若小船在D处时恰好是上午11点，问渔船能否在下午5点之前到达E处？请说明理由．
(1)求BC的距离；（结果保留整数）
解：过点作CF⊥AB，由题意得AB=1×60=60 (海里)，在A处测得小岛C在北偏东45°方向，则∠CAF=45°，在B处测得小岛C在北偏东30°方向，则∠CBF=60°，设 海里，在 中， ，则 ， ,则在 中， ，则 ，
且 答：BC的距离为164海里；
（2）解：与小岛C最近的D处，即CD⊥BE，在B处沿北偏东75°方向继续航行，则∠CBD= ∠BCD= 45°,在小岛C加油后，再沿南偏东75°方向航行，则∠ECF= 75°，∴ ∠ECD= 30°+ 75°-45°=60°，∠CED= 90°-60°=30°由（1）得BC的距离为164海里，在 中， ，在 中，∠CED=30°， ∴∴渔船所用时间为：
5. 如图，某火车站A位于东西方向火车轨道l上，小区B在火车站A的西北方向400米处，小区C在火车站A的北偏东15°方向上，小区C在小区B的北偏东60°方向上．
(1)求火车站A与小区C之间的距离（精确到1米）； (2)火车在行驶过程中，周围300米内都能听到它发出的噪声，深夜更加明显，一列火车从火车站A向西行驶，火车发出的噪声会影响小区B的住户吗？如果受到影响，需要在轨道旁安装降噪装置，请求出需安装降噪装置的轨道长度；如果不受影响，请说明理由（参考数据： ）．
(1)求火车站A与小区C之间的距离（精确到1米）；
解：根据题意，得∴过点B作BD⊥AC于点D，∴∴CD=BD∴AB=400m∴AD=200m，∴