2023年广东省深圳市福田区中考二模数学试题（含答题卡）

这是一份2023年广东省深圳市福田区中考二模数学试题（含答题卡），文件包含参考答案及评分标准docx、数学试卷docx、数学答题卡pdf等3份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。
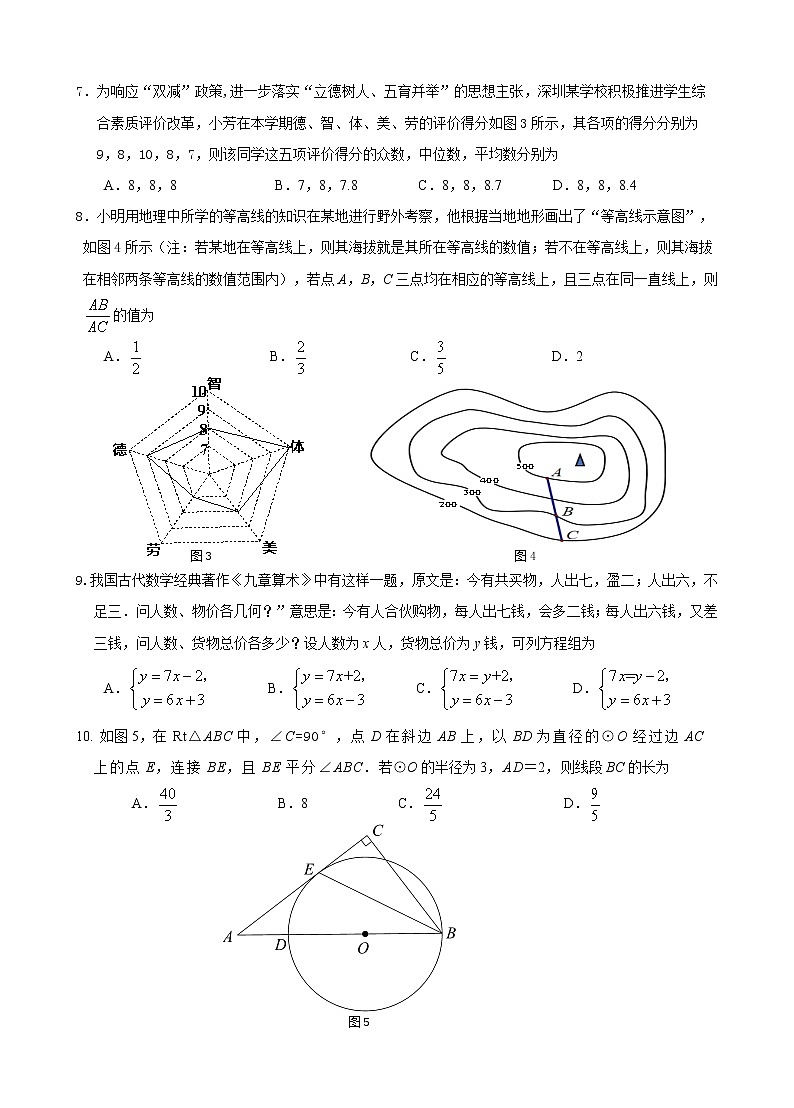
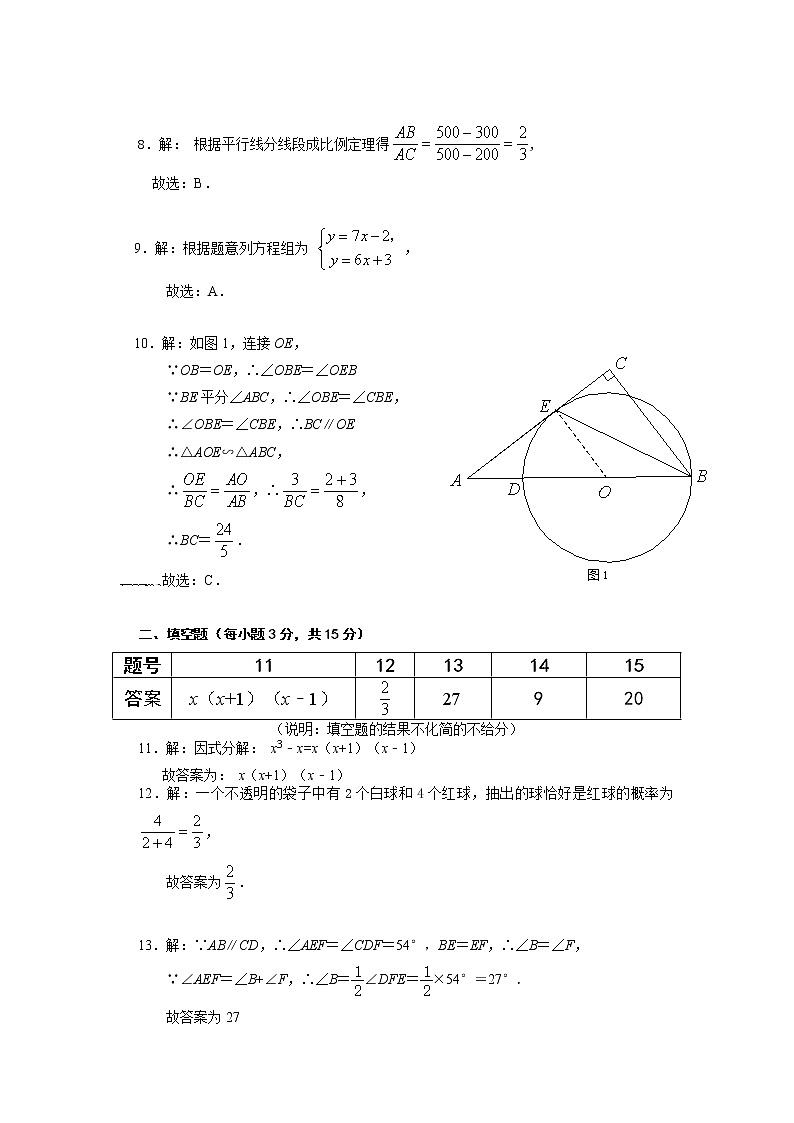
2022-2023学年九年级教学质量检测参考答案及评分标准一、选择题（每小题3分，共30分）题号12345678910答案ADBBCA DBAC1．解：点A表示的数为3，3的相反数为﹣3，故选：A． 2．解：这个几何体的俯视图为：故选：D． 3．解：将66000 用科学记数法表示为6.6×104，故选：B． 4．不等式组的解集是，故选：B． 5．解：∵a2•a6＝a8，∴A选项的结论不符合题意；∵a8÷a4＝a8﹣4＝a4，∴B选项的结论不符合题意；∵（﹣2a2）3＝﹣8a6，故C符合题意；∵a3与a4不属于同类项，不能合并，故D不符合题意，故选：C． 6．解：根据基本作图，A选项作AD平分∠CAB，B、D选项中为过A点作BC的垂线，C选项作BC的垂直平分线得到BC边上的中线AD， 故选：A．  7．解：该同学五项评价得分分别为7，8，8，9，10，出现次数最多的数是8，所以众数为8，位于中间位置的数是8，所以中位数是8，平均数为＝8.4，故选：D． 8．解： 根据平行线分线段成比例定理得,故选：B． 9．解：根据题意列方程组为 ，故选：A． 10．解：如图1，连接OE，∵OB＝OE，∴∠OBE＝∠OEB∵BE平分∠ABC，∴∠OBE＝∠CBE，∴∠OBE＝∠CBE，∴BC∥OE∴△AOE∽△ABC，∴，∴，∴BC＝．声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/4/4 3:36:27；用户：龚天青；邮箱：gongtq_yl@xyh.com学号：2037998故选：C． 二、填空题（每小题3分，共15分）题号1112131415答案x（x+1）（x﹣1）27920（说明：填空题的结果不化简的不给分）11．解：因式分解： x3﹣x=x（x+1）（x﹣1）故答案为： x（x+1）（x﹣1）12．解：一个不透明的袋子中有2个白球和4个红球，抽出的球恰好是红球的概率为，故答案为． 13．解：∵AB∥CD，∴∠AEF＝∠CDF＝54°，BE＝EF，∴∠B＝∠F，∵∠AEF＝∠B+∠F，∴∠B＝∠DFE＝×54°＝27°．故答案为27 14．解：∵菱形ABCD，A（﹣6，6），B（﹣3，2），∴D（﹣1，6），C（2，2），向右平移a个单位，得到D’（﹣1+a，6），C’（2+a，2），∵向右平移使顶点C，D两点都落在反比例函数（k≠0，x＞0）的图象上，∴6 (﹣1+a)= 2（2+a）, ∴a =，∴k=9，故答案9．15．解：如图2，∵四边形ABCD是正方形，∴AO＝CO＝BO＝DO，AC⊥BD，∠OBD＝∠OCD＝45°，∴∠BOC＝∠MON＝90°，∴∠MOB＝∠NOC，∴△BOM≌△CON，∴OM=ON，∵∠MON＝90°，∴∠OMN＝45°，∠OCM＝45°，∴∠OMN＝∠OCM，∵∠MOP＝∠COM，∴△OPM∽△OMC， ∴OM2＝OP•OC，过点O作OH⊥CB于H，∵正方形ABCD的边长为8，∴BH=OH=4, ∵BM＝2，∴MH＝2，∴OM2＝22+42＝20，∴OP•OC＝20．故答案20． 三、解答题16．（5分）解：原式＝4﹣2﹣1+6×………………1+1+1+1分＝﹣4﹣2﹣1+2＝3．………………1分，累计5分17．（7分）解：原式=﹣，………………3分，＝﹣，…………2分，累计5分＝，………………1分，累计6分当a＝3时，原式=．…………1分，累计7分 18．（8分）解：（1）∵被抽取的学生总人数为20÷0.05＝400（名），∴a＝400×0.3＝120． b＝140÷400=0.35，故答案为：120； 0.35，………2+2分，累计4分（2）补全频数分布直方图如下图：………2分，累计6分（3）15000×(0.1+0.3)=6000人答：估计今年该区初三学生中，每天课外阅读小于1小时的学生约有6000人…………………………1+1分，累计8分19．（8分）解：（1）设洋红风树苗的单价是x元，则紫花风树苗的单价是（1+50%）x元，由题意得：，…………2分，解得：x＝60，经检验．x＝60是原方程的解，且符合题意，…………1分，累计3分∴（1+50%）x＝1.5×60＝90，答：紫花风树苗的单价是60元，洋红风树苗的单价是90元．…………1分，累计4分（2）设购买m棵洋红风树苗，则购买（120﹣m）棵紫花风树苗，由题意得：60m+90（120﹣m）≤8700，…………2分，累计6分解得：m≥70，…………1分，累计7分答：至少购买70棵洋红风树苗．…………1分，累计8分 20．（8分）解：（1）由题意，抛物线y＝a(x﹣1)2+h与x轴交于点A（﹣2，0），与y轴交于点C（0，4），则  …………1分      解之，得   …………2分，累计3分      ∴该抛物线的表达式为…………1分，累计4分（2）当y=0时，，解得：x1=﹣2，x2=4，       ∴ A（﹣2，0），B（4，0）又∵点E是线段BC的中点，∴E（2，2），   …………1分，累计5分设直线AE的解析式为：y=kx+b，，解得直线AE的解析式为，…………1分，累计6分，解得 …………1分，累计7分   由图可得点D的坐标为（3，）              …………1分，累计8分 21．（9分）（1）解：（1）∵圆弧AB长为250海里，它所对的圆心角为90°，圆的半径为r，∴ , …………2分，解得r=500(海里）答：该圆弧AB所在圆的半径r为500海里.  …………1分，累计3分（2）结论：图中点E表示所建补给站；线段EF表示最短运输路线．…………1+1分，累计5分如图3，简要画法：先找出圆心O，作OE⊥m于点E，交圆弧AB于点F,则图中点E表示所建补给站；线段EF表示最短运输路线．（其他画法参考给分）（3）(法一)如图4，作ATOE于点T，作BUOE于点U，∵∠AOB=90°，∴∠OAT+∠AOT=∠BOU+∠AOT=90°，∴ ∠OAT=∠BOU，又∵OA=OB，∴△ATO≌△OUB，∴AT=OU，OT=BU，…………2分，累计7分∵AC=ET=600海里，BD=UE=500海里，∴UT=100海里设线段OT长为x海里，则线段AT长为（100+x）海里，由+(x+100)2=5002, ∴（舍去），∴OT=300海里，∴OE=OT+AC=900海里，∴FE=OE﹣r=900﹣500=400海里.……2分，累计9分 (法二)如图5，过点O作MN//CD分别交CA，DB的延长线于点M，N，∵∠ACD=∠BDC=90°，∴四边形CDNM是矩形，∵∠AOB=90°，∠MAO+∠AOM=∠BON+∠AOM=90°，∴ ∠MAO=∠BON，又∵OA=OB，∠M=∠N=90°，∴△AMO≌△ONB，∴AM=ON，OM=BN，…………2分，累计7分∵AC=600海里，BD=500海里，设线段AM长为x海里，∴AM=ON=x海里，∴CM= DN= OE=（600+x）海里，∴BN=(600+x-500) 海里=(100+x) 海里, ∵∠N=90°,∴ON2+BN2=OB2，∴+(x+100)2=5002，∴（舍去），∴AM=300海里， ∴CM=AM+AC=900海里，∴OE=CM=900海里，∴FE=OE﹣OF=900﹣500=400海里. …………2分，累计9分 22．（10分）（1）① ；②.…………1+2分，累计3分（2）scop.…………1分，累计4分理由如下：如图6，连结FP.∵ 点C是AP的中点，△ACE，△CDF都是等边三角形，∴ CP=EC，,又,∴ △ECF≌△PCF.∴  ∠EFC=∠PFC，…………………1分，累计5分同理，∠GFD=∠PFD，∴  ∠EFG=2∠CFD=，∴  scop=scop.…………………1分，累计6分(3)  △EPG的周长是；…………………2分，累计8分此时，AP的长为4或8. …………………1+1分，累计10分 理由：如图7，∵ △ECF≌△PCF.∴ EF=PF,同理可证：GF=PF,∴ EF=GF,∵∠EFG=，EF=， ∴EG==，∵点C，D分别是线段AP，BP的中点，等边三角形△ACE，△CDF，△DBG的边长分别为a，b，c，∴PC=AC=CE=a,PD=BD=DG=c,∠ECP=∠PDG=，∴EP=,PG=,∴EP+PG=,∴EG+EP+PG=.（法一）如图7，过点F作垂直CE的延长线于点H,∵CF=CD=b==6，∠ECF=60O，∴FH=CFsin60O=3,CH=CFcos60O=3,在Rt△EFH中，HE=，∴CE=CH﹣HE=3-1=2, ∴AP=2CE=4,因为对称性，AP=12﹣4=8,  ∴AP=4或8.（法二）如图8，∵CE=CP, ∠ECO=∠PCO=60°，∴CF⊥PO, ∴CO=EO=∴OF=CF﹣CO=由勾股定理得：∴∴AP=4或8.