河北省石家庄市赵县2022-2023学年七年级下学期（3月）自我评价数学试卷(含解析)

2022—2023学年度第二学期自我评价①

七年级数学试卷

一、选择题（本大题有16个小题，共42分．1～10小题各3分，11～16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔将正确选项涂黑）

1. 下列命题是假命题是（    ）

A. 同旁内角互补，两直线平行；

B. 如果两条直线都和第三条直线平行，那么这两条直线也互相平行；

C. 同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行；

D. 同位角互补，两直线平行；

2. “小小竹排江中游，巍巍青山两岸走”，所描绘的图形变换主要是（  ）

A. 平移变换 B. 翻折变换 C. 旋转变换 D. 以上都不对

3. 下列四个图形中，与是对顶角是（    ）

A.  B.  

C.  D.

4. 的平方根是（   ）

A. −0.7 B. +0.7 C.  D. 0.49

5. 下列图形中，∠1与∠2是同位角的是（　　）

A.  B.

C.  D.

6. 如图所示，直线与相交形成了、、和中，若要确定这四个角的度数，至少要测量其中的（    ）

A. 个角 B. 个角 C. 个角 D. 个角

7. 在如下所示的条件中，可以判断两条直线互相垂直的是（    ）

①两直线相交所成的四个角都是直角；

②两直线相交，对顶角互补；

③两直线相交所成的四个角都相等．

A. ①② B. ①③ C. ②③ D. ①②③

8. 下列图形中，线段MN的长度表示点M到直线l的距离的是（     ）

A.  B.  

C.  D.

9. 试说明“若，，，则”是真命题．以下是排乱的推理过程：

①因为（已知）；

②因为，（已知）；

③所以，（等式性质）；

④所以（等量代换）；

⑤所以（等量代换）．

正确的顺序是(   )

A. ①→③→②→⑤→④ B. ②→③→⑤→①→④

C. ②→③→①→⑤→④ D. ②→⑤→①→③→④

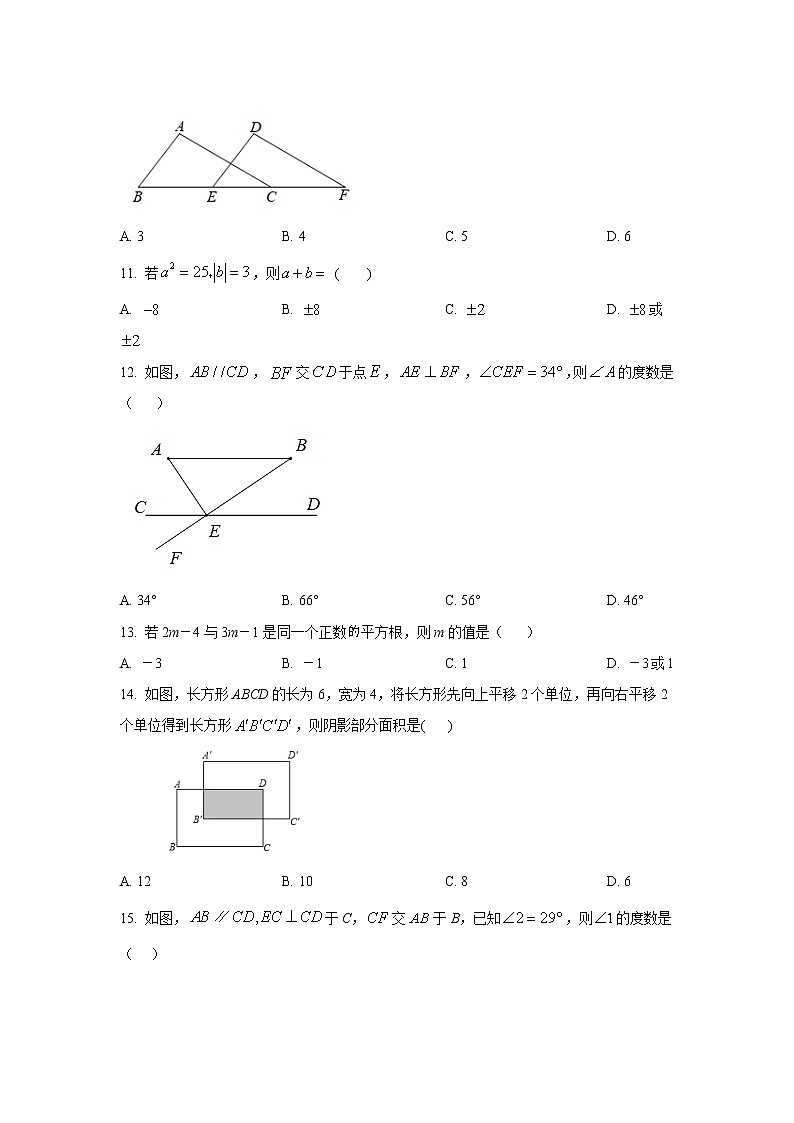
10. 如图，沿直线向右平移得到，已知，，则的长为（    ）

A. 3 B. 4 C. 5 D. 6

11. 若，则 (　　)

A.  B.  C.  D. 或

12. 如图，，交于点，，，则的度数是（    ）

A. 34° B. 66° C. 56° D. 46°

13. 若2m－4与3m－1是同一个正数平方根，则m的值是（    ）

A. －3 B. －1 C. 1 D. －3或1

14. 如图，长方形ABCD的长为6，宽为4，将长方形先向上平移2个单位，再向右平移2个单位得到长方形，则阴影部分面积是(    )

A. 12 B. 10 C. 8 D. 6

15. 如图，于C，交于B，已知，则的度数是（   ）

A.  B.  C.  D.

16. 如图，P是∠ABC内一点，点Q在BC上，过点P画直线a∥BC，过点Q画直线b∥AB，若∠ABC=115°，则直线a与b相交所成的锐角的度数为（　　）

A. 25° B. 45° C. 65° D. 85°

二、填空题（本大题有3个小题，每小题有2个空，每空2分，共12分）

17. 81的平方根是_____；的算术平方根是_____．

18. 如图，甲、乙两只蚂蚁在两条平行马路同一侧的，两点处，比赛看谁先横过马路．如果它们同时出发，速度一样，都走最近的道路，结果是______，依据是________________________．

19. 如图，若，则______，依据是__________________．

三、解答题（本大题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤）

20. 求下列各数平方根：

（1）121；

（2）；

（3）；

（4）．

21. 如图，已知：点A、点B及直线l．

（1）请画出从点A到直线l的最短路线，并写出画图的依据．

（2）请在直线l上确定一点O，使点O到点A与点O到点B的距离之和最短，并写出画图的依据．

22. 如图，与互补，．

那么．

证明如下：∵（已知），

∴______(   )

∴(   )

∵（已知）

∴(   )

∴____________(   )

∴(   )

23. 如图，和相交于点，平分，于点，，求的度数．

24. 如图，AB、CD交于点O，∠1=∠2，∠3：∠1=8：1，求∠4的度数． 

25. 如图，EF//AD，AD//BC，CE平分∠BCF，∠DAC＝120°，∠ACF＝20°，求∠FEC的度数．

26. 已知，在下列各图中，点O为直线AB上一点，∠AOC＝60°，直角三角板的直角顶点放在点O处．

（1）如图1，三角板一边OM在射线OB上，另一边ON在直线AB的下方，则∠BOC的度数为　 　°，∠CON的度数为　 　°；

（2）如图2，三角板一边OM恰好在∠BOC的角平分线OE上，另一边ON在直线AB的下方，此时∠BON的度数为　 　°；

（3）在图2中，延长线段NO得到射线OD，如图3，则∠AOD的度数为　 　°；∠DOC与∠BON的数量关系是∠DOC    ∠BON（填“＞”、“＝”或“＜”）；

（4）如图4，MN⊥AB，ON在∠AOC的内部，若另一边OM在直线AB的下方，则∠COM+∠AON的度数为     °；∠AOM﹣∠CON的度数为　 　°

答案

1. D

解：A、同旁内角互补，两直线平行；是真命题，不合题意；

B、如果两条直线都与第三条直线平行，那么这两条直线也互相平行，是真命题，不合题意；

C、同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行，是真命题，不合题意；

D、同位角相等，两直线平行；故同位角互补，两直线平行是假命题，符合题意，

故选D．

2. A

解：“小小竹排水中游，巍巍青山两岸走”所描绘的图形变换主要是平移变换，
故选：A．

3. D

解：由对顶角的定义可知，四个图形中D中∠1与∠2为对顶角．

故选：D．

4. C

，，

的平方根是．

故选C．

5. B

解：A、∠1与∠2的对顶角是同位角，故本选项不符合题意；

B、∠1与∠2同位角，故本选项符合题意；

C、∠1与∠2是内错角，故本选项不符合题意；

D、∠1与∠2是同旁内角，故本选项不符合题意．

故选：B．

6. A

根据题意可得，,

∴要确定这四个角的度数，至少要测量其中的个角即可.

故选

7. D

解：∵因为两直线相交所成的四个角都是直角，即四个角都是，

所以两条直线互相垂直．

①结论符合题意．

两直线相交，对顶角互补，（对顶角相等）

两条直线相交所成的对顶角是．

所以两条直线互相垂直．

②结论符合题意．

两直线相交所成的四个角都相等，

四个角都是．

所以两条直线互相垂直．

③结论符合题意．

故选：D．

8. A

解：图B、C、D中，线段MN不与直线l垂直，故线段MN的长度不能表示点M到直线l的距离；

图A中，线段MN与直线l垂直，垂足为点N，故线段MN的长度能表示点M到直线l的距离．故选A．

9. C

证明：因为，（已知），

所以，（等式的性质）；

因为（已知），

所以（等量代换）．

所以（等量代换）．

∴排序顺序为：②→③→①→⑤→④．

故选C．

10. A

解：∵沿直线向右平移得到，

∴，

∵，

∴，

∴，

故选A．

11. D

解：，，

，；，；，；，，

则或．

故选：D．

12. C

解：∵，，

∴，

∵，

∴，

故选：C

13. D

当时，；

当时，；

故选：D.

14. C

解：∵长方形ABCD先向上平移2个单位，再向右平移2个单位得到长方形A′B′C′D′，
∴AB∥A′B′，BC∥B′C′，
∴A′B′⊥BC，
延长A′B′交BC于F，AD交A′B′于E，CD交B′C′于G，

∴FB′=2，AE=2，
易得四边形ABFE、四边形BEDG都矩形，
∴DE=AD-AE=6-2=4，B′E=EF-B′F=AB-B′F=4-2=2，
∴阴影部分面积=4×2=8．
故选C．

15. C

延长到F，

∵，

∴，

∵，

∴，

∵，

∴．

故选C．

16. C

解：∵b∥AB，

∴∠1+∠B=180°，

∵∠ABC=115°，

∴∠1=65°，

∵a∥BC，

∴∠2=∠1=65°，

故选：C．

17. ①. ±9    ②. 2

81的平方根是=±9；

的算术平方根是4，4的算术平方根即为2；

故填±9；2．

18. ①. 同时到达    ②. 平行线间的距离处处相等

解：∵点到直线之间，垂线段最短，

∴两只蚂蚁走的都是垂线段，

∵平行线间的距离处处相等，它们同时出发，速度一样，

∴它们同时到达；

故答案为：同时到达，平行线间的距离处处相等．

19. ①.     ②. 内错角相等，两直线平行

解：若，，依据是内错角相等，两直线平行．

故答案为：，内错角相等，两直线平行．

20. （1）

解：；

（2）

；

（3）

；

（4）

．

21. （1）如图所示：点E为所求，根据垂线段最短；

（2）如图所示：根据两点之间线段最短．

22. 证明：∵（已知），

∴（同旁内角互补，两直线平行），

∴（两直线平行，同位角相等），

∵（已知），

∴（等量代换），

∴（内错角相等，两直线平行），

∴（两直线平行，同位角相等）．

23. 解：∵，

∴，

∵和相交于点，

∴，

∵平分，

∴，

∴．

24. ∵∠1+∠2+∠3=180°，

又∵∠1=∠2，∠3：∠1=8：1，即∠3=8∠1，

∴∠1+∠1+8∠1=180°，

即∠1=18°，

∴∠4=∠1+∠2=36°．

25. ∵EF∥AD，AD∥BC，

∴EF∥BC，

∴∠ACB＋∠DAC＝180°，

∵∠DAC＝120°，

∴∠ACB＝60°，

又∵∠ACF＝20°，

∴∠FCB＝∠ACB−∠ACF＝40°，

∵CE平分∠BCF，

∴∠BCE＝20°，

∵EF∥BC，

∴∠FEC＝∠ECB，

∴∠FEC＝20°．

26. 解：（1）∵∠AOC=60°，∠BOC与∠AOC互补，∠AON=90°，

∴∠BOC=180°﹣60°=120°，∠CON=∠AOC+∠AON=60°+90°=150°．

故答案为120；150；

（2）∵三角板一边OM恰好在∠BOC的角平分线OE上，

由（1）得∠BOC=120°，

∴∠BOM=∠BOC=60°，

又∵∠MON=∠BOM+∠BON=90°，

∴∠BON=90°﹣60°=30°．

故答案为30°；

（3）∵∠AOD=∠BON（对顶角），∠BON=30°，

∴∠AOD=30°，

又∵∠AOC=60°，

∴∠DOC=∠AOC﹣∠AOD=60°﹣30°=30°=∠BON．

故答案为30，=；

（4）∵MN⊥AB，

∴∠AON与∠MNO互余，

∵∠MNO=60°（三角板里面的60°角），

∴∠AON=90°﹣60°=30°，

∵∠AOC=60°，

∴∠CON=∠AOC﹣∠AON=60°﹣30°=30°，

∴∠COM+∠AON=∠MON+2∠CON=90°+2×30°=150°，

∴∠AOM﹣∠CON=∠MON﹣2∠CON=90°﹣2×30°=30°．

故答案为150；30．