初中人教版 (五四制)20.2 画轴对称图形完美版ppt课件

20.2 画轴对称图形

第一课时

一、教学目标

（一）学习目标

1．通过实际操作，了解什么叫做轴对称变换.

2．掌握作一个图形关于一条直线的轴对称图形的方法.

3．经历实际操作，发展学生的空间思维，并体会轴对称变换在实际生活中的应用.

（二）学习重点

   如何做已知图形关于一条直线的轴对称图形.

（三）学习难点

   利用轴对称变换作图并理解轴对称变换的实际作用.

二、教学设计

（一）课前设计

1.预习任务

一个图形与另一个图形沿着某条直线折叠后能完全重合，那么就说这两个图形关于这条直线成轴对称 ，折痕所在的直线就是它们的 对称轴 ，并且连接任意一对对称点的线段被对称轴 垂直平分 ；已知图形和对称轴作对称图形，先作已知图形中每个  特殊点 关于对称轴的对称点，再 连接 对称点得其对称图形.

2.预习自测

（1）如图，图中的两个脚印沿着直线l对折后能够完全重合，那么这两个脚印关于直线l __________，直线l叫做它们的_________，点P和点 是一对_________，线段P被直线l_____________.

【知识点】轴对称的图形的相关性质

【解题过程】成轴对称的两个图形形状、大小完全相同；新图形上的每一点都是原图形上的某一点关于直线l的对称点；连接任意一对对应点的线段被对称轴垂直平分.

【思路点拨】利用轴对称图形的相关性质进行分析.

【答案】成轴对称，对称轴，对称点，垂直平分

（2）如图，△ABC与△关于直线l对称那么AO__直线l ,AO__.

【知识点】轴对称图形的对应点之间的线段被对称轴垂直平分

【解题过程】△ABC与△关于直线l对称，那么A被直线l垂直平分，所以AO=

【思路点拨】轴对称的两个图形的所有对应点之间的线段被对称轴垂直平分.

【答案】⊥，=

（3）把以下图形补成关于直线l对称的图形

【知识点】轴对称图形的画法

【解题过程】分别作出△ABC三个顶点的对称点，并顺次连接这些对称点.

【思路点拨】作点的对称点的方法是：作垂直，顺延长，取相等.

【答案】           

（4）要在燃气管道l上修建一个泵站，分别向A、B两镇供气，泵站修建在管道的什么位置可以使输气管线最短.

【知识点】利用轴对称解决最短路径问题

【解题过程】作点A的对称点C，并连接BC，与直线l交于点P即为所求.

【思路点拨】两条线段之和为“最短”问题，一般采用对称法进行转化.

【答案】              

（二）课堂设计

1.知识回顾

（1）轴对称：一个图形沿着某条直线对折能和另外一个图形重合．

（2）轴对称的两个图形的每一对对应点之间的线段被对称轴垂直平分．

（3）线段的垂直平分线的性质：垂直平分线上的点到线段两个端点的距离相等.

2.问题探究

探究一 感知轴对称变换.

●活动①动手操作，整合旧知

师：在一张半透明的纸的左边画上一个三角形，把这张纸对折后描图，打开这张纸，就能得到相应的另外一个三角形.

请问（1）这两个三角形有什么关系．（2）这条折痕和这两个三角形有什么关系. （3）图中的点A和点D之间的连线和折痕有什么关系.

教师总结：△ABC与△DEF关于直线l对称，直线l叫做对称轴，并且线段AD、BE、CF被直线l垂直平分.

【设计意图】动手操作，感知轴对称变换

●活动②探究并归纳轴对称的性质

师问：画出的轴对称图形的大小、形状与原图形有怎样的关系？画出的轴对称图形的点与原图形上的点有什么关系？对应点所连线段与对称轴有什么关系？

学生回答：由一个平面图形可以得到与它关于一条直线l 对称的图形，这个图形与原图形的形状、大小完全相同；新图形上的每一点都是原图形上的某一点关于直线 l 的对称点；连接任意一对对应点的线段被对称轴垂直平分．

师问：如果有一个图形和一条直线，如何作出这个图形关于这条直线对称的图形呢？

教师总结：对于某些图形，只要画出图形中的一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形．

【设计意图】归纳轴对称图形的性质，提炼画轴对称图形方法.

探究二 画轴对称图形的方法. ★

●活动①大胆猜想，探究新知识

师问：已知一个点和一条直线，如何画出这个点关于这条直线的对称点？

学生回答：由于对称点的连线被对称轴垂直平分，所以先过点M作直线l的垂线，垂足为O，在垂线上截取ON=OM，N就是点M关于直线l的对称点.

教师总结新知：

作点的对称点的方法：过原点作对称轴的垂线，并延长，在延长线上截取一段与原点和垂足之间的距离相等的线段，截取线段的非垂足端点即为对称点.简要总结为：作垂线、顺延长、取相等.

师问：我们如何验证M、N是一对对称点？

学生回答：沿着直线l折叠，观察点M、N能否重合.

【设计意图】掌握对称点的作法，为作对称图形做准备.

●活动②集思广益，探究新知.

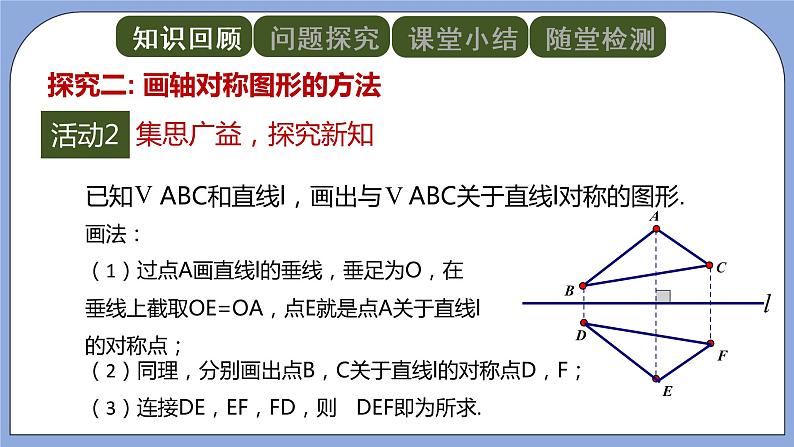
师问：已知△ABC和直线l，画出与△ABC关于直线l对称的图形.

学生回答：△ABC可以由三个顶点的位置确定，只要能分别画出这三个顶点的对称点，再连接这些对称点，就可以得到要画得对称图形.

教师总结方法：画法（1）过点A画直线l的垂线，垂足为O，在垂线上截取OE=OA，点E就是点A关于直线l的对称点；

（2）同理，分别画出点B，C关于直线l的对称点D，F；

（3）连接DE，EF，FD，则△DEF即为所求.

【设计意图】掌握作对称图形的一般方法.

●活动③反思过程，总结方法.

思考：几何图形的对称图形的做法？

学生回答：找关键点的对称点，然后进行连接，得到新图形.

教师归纳：几何图形都可以看作由点组成，对于某些图形，只要画出图形中的一些特殊点的对称点，连接这些对称点，就可以得到原图形的轴对称图形.

【设计意图】通过师生合作，进一步归纳新知.

●活动④发散思维，重新认识.

师问：已知一个几何图形在对称轴两侧，如何作出它的轴对称图形呢？

学生回答：找关键点，作出关键点的对称点，连接这些对称点即可.

教师展示图形：作出△ABC关于直线AD的轴对称图形.

学生尝试独立解决：

教师展示结果：

探究三 熟练掌握轴对称图形的画法，并会运用轴对称图形的相关性质解决实际问题.★▲

●活动① 作轴对称图形（部分点在对称轴上）

例1把以下图形补成关于直线l对称的图形.

【知识点】 轴对称图形的画法

【解题过程】过点E作直线l的垂线，垂足为O，并截取OH=OE，点H即为点E的对称点，同理作出点F的对称点I，连接HG、GI、HI，△HGI即为所求.

【思路点拨】找准必要的关键点，已知一点在对称轴上，只需分别画出另外两点的对称点即可，对称点的做法：作垂直，顺延长，取相等.

【答案】              

练习：已知BC⊥AC，把以下图像补成关于直线l对称的图形.

【知识点】轴对称图形的画法

【解题过程】根据题意，只需延长BC，并在延长线上截取CD=CB，连接AD、DC，△ACD即为所求.

【思路点拨】作点的对称点的方法：作垂直，顺延长，取相等.

【答案】                   

【设计意图】尝试练习，掌握轴对称图形的画法.

●活动2作轴对称图形（图形与对称轴无交点）

例2  画出∠ABC关于直线l的对称图形.

【知识点】轴对称图形的画法.

【解题过程】在∠ABC中，取点A、C，分别作出点A、B、C的对称点D、E、F，连接点EF，ED，由于角的两边是射线，所以只需将EF、ED延长即可，所得的∠DEF即为所求.

【思路点拨】要确定一个角的位置，只需确定它的顶点与两条边，所以在两条边上分别取一点，然后把它们以及顶点的对称点作出来，再连接这些对称点，最后把角的两边延长.

【答案】              

练习：如图，作出菱形ABCD关于直线l的对称图形.

【知识点】轴对称图形的画法.

【解题过程】分别作出点A、B、C、D关于直线l的对称点E、F、G、I，连接EF，FG，GI，IE，菱形EFGI即为所求.

【思路点拨】作出菱形四个顶点的对称点，并顺次连接起来．

【答案】              

【设计意图】让学生熟练轴对称图形的画法.

●活动3 利用轴对称解决“最短”问题

例3 如图，请在直线l上找一点P，使得点P分别到点A、到点B的距离之和最短.

【知识点】对称点之间的连线被对称轴垂直平分，垂直平分线上的点到线段两端点的距离相等，两点之间线段最短.

【解题过程】作点A关于直线l的对称点C，连接BC与直线l交于点P，则点P即为所求．

【思路点拨】 假定已找到的点P，使得PA+PB为最短，根据两点之间线段最短，可想办法将PA与PB转化到一条直线上，故作点A的对称点C，PA就转化为PC，只需连接BC，BC与直线l的交点即为点P.

【答案】

练习：如图所示，要在河边建立一个水站向A，B两个村庄供水，请问水站建在河边的哪个地方更经济实惠？

 【知识点】对称点之间的连线被对称轴垂直平分，垂直平分线上的点到线段两端点的距离相等，两点之间线段最短.

【解题过程】根据题意要经济实惠，那么需要PA+PB最短，转化为最短路径问题.作点A关于直线l的对称点C，连接BC与直线l交于点P，则点P即为所求，两条线段之和为“最短”问题一般采用对称法.

【思路点拨】两条线段不在一条直线上，利用轴对称将其转化到一条直线上，再根据两点之间线段最短求得点P.

【答案】             

【设计意图】根据轴对称图形画法的学习，让学生掌握解决最短路径问题的方法.

3. 课堂总结

知识梳理

（1）已知图形和对称轴作轴对称图形：作已知图形中的每个关键点关于对称轴的对称点，再连接对称点得到对称图形.

（2）两条线段之和为“最短”问题，一般采用对称法.

重难点归纳

（1）会作轴对称图形．

（2）利用对称法解决最短路径问题.

（三）课后作业

基础型 自主突破

1.把以下图形补成关于直线l对称的图形.

【知识点】轴对称图形的画法.

【解题过程】找到原图形的关键点，并作出他们关于直线l的对称点，并连接这些对称点.

【思路点拨】画对称点的方法：作垂直，顺延长，取相等.

【答案】                

2.把以下图形补成关于直线l对称的图形.

【知识点】轴对称图形的画法

【解题过程】只需作出点B关于直线l的对称点E，分别连接AE、CE即为所求.

【思路点拨】找准某些关键点即可.

【答案】          

3.把以下图形补成关于直线l对称的图形.

【知识点】轴对称图形的画法

【解题过程】分别作出点A、点B的对称点，再顺次连接CO、OD、DC即为所求.

【思路点拨】点O在对称轴上，只需作出A、B两点的对称点.

【答案】                     

4.把以下图形补成关于直线l对称的图形.

【知识点】轴对称图形的画法

【解题过程】把不在对称轴上的关键点关于直线l的对称点作出来，再进行顺次连接.

【思路点拨】找准图形的关键点，再作对称点.

【答案】                     

5.小莹和小博士下棋，小莹执白子，小博士执黑子．如图，棋盘中心黑子的位置用（-1，0）表示，右下角黑子的位置用（0，-1）表示．小莹将第4枚白子放入棋盘后，所有棋子构成一个轴对称图形．他放的位置是（　　）

A．（-2，1） B．（-1，1） C．（1，-2） D．（-1，-2）

【知识点】坐标与图形变化-对称；坐标确定位置．

【解题过程】棋盘中心黑子的位置用（-1，0）表示，则这点所在的横线是x轴，右下角黑子的位置用（0，-1），则这点所在的纵线是y轴，则当放的位置是（-1，1）时构成轴对称图形．故选B.

【思路点拨】本题考查了轴对称图形和坐标位置的确定.

【答案】B

6.如图,△ABC关于直线l的对称图形是△DEF，下列判断错误的是（   ）

A. AB=DE   B.BC∥EF  C.直线l⊥BE   D.∠ABC=∠DEF

【知识点】轴对称图形的相关性质

【解题过程】成轴对称的图形是全等形，故AB=DE，∠ABC=∠DEF，对称点之间的线段被对称轴垂直平分即直线l⊥BE，而BC∥EF没有依据，故B选项错误.

【思路点拨】结合轴对称图形的相关性质逐一检验，从而找到合理答案.

【答案】B

能力型 师生共研

7.已知△ABC和直线m，n，先作△关于直线m的对称图形△DEF，再作△DEF关于直线n的对称图形△GHI.

【知识点】轴对称图形的画法

【解题过程】依次作出△ABC关于直线m的对称图形，然后再作出关于直线n的对称图形.

【思路点拨】确定三角形位置的要素是顶点，故作顶点的对称点是关键.

【答案】          

8.已知△ABC和直线m，n，先作△关于直线m的对称图形△DEF，再作△DEF关于直线n的对称图形△GHI.

【知识点】轴对称图形的画法

【解题过程】依次作出△ABC关于直线m的对称图形，然后再作出关于直线n的对称图形.

【思路点拨】确定三角形位置的要素是顶点，故作顶点的对称点是关键.

【答案】          

【设计意图】熟练轴对称图形的画法.

探究型 多维突破

9.直线l左侧有两点P、Q，试在直线上确定一点O，使得OP+OQ最短.

【知识点】轴对称变换的运用

【解题过程】作点P关于直线l的对称点A，连接AQ交直线l与点O即为所求.

【思路点拨】利用轴对称解决最短路径问题.

【答案】                  

10.如图，△ABC与△DEF关于某条直线对称，请画出对称轴.

【知识点】任意一对对应点之间的连线被对称轴垂直平分

【解题过程】连接AD，作线段AD的垂直平分线.

【思路点拨】根据对称图形确定对称轴的位置，注意垂直平分线的画法.

【答案】             

【设计意图】让学生掌握轴对称的运用，加深对知识的巩固.

自助餐

1.观察下图中各组图形，其中不是轴对称的是（　　）

A. B. C.  D.

【知识点】轴对称图形的判断

【解题过程】由图形可以看出：C选项中的伞把不对称，故选C．

【思路点拨】熟练运用轴对称图形的概念.

【答案】C

2.把以下图形补成关于直线l的对称图形.

【知识点】轴对称图形的画法

【解题过程】找关键点，作它的对称点，然后顺次连接图形即为所求.

【思路点拨】本题只需找准一个关键点即可.

【答案】                   

3.下图是汉字“中”的一半，请补全该汉字.

【知识点】轴对称图形的画法

【解题过程】根据题意，只需将延长上下两条线段，并截取相等线段，找到对称点，然后进行连接即可.

【思路点拨】利用“中”字是轴对称图形进行图形的补充.

【答案】

4.画出圆关于直线l的对称图形.

【知识点】轴对称图形的画法

【解题过程】要确定一个圆，只需找准它的圆心和半径，这里要画它的轴对称图形，只需作出圆心O和半径的另一个端点A的对称点，在用圆规进行画圆，画出的圆即为所求.

【思路点拨】确定圆的两个要素：圆心和半径.

【答案】       

5.已知∠AOB，试确定它的对称轴.

【知识点】作轴对称图形的对称轴

【解题过程】分别在OA，OB上截取线段OM=ON，连接MN，作线段MN的垂直平分线即为所求.

【思路点拨】角是轴对称图形，它的对称轴即角平分线所在的直线.

【答案】

6.如图，A、B为重庆市内两个较大的商圈，现需要在主要交通干道l上修建一个轻轨站P，问如何修建，才能使得人们出行逛街更便捷.

【知识点】利用轴对称解决最短路径问题

【解题过程】作点A关于直线l的对称点A’，再连接A’B，交直线l于点P，点P即为所求.

【思路点拨】利用轴对称解决两条线段之和“最短”问题.

【答案】