人教版 (五四制)八年级上册20.3 等腰三角形完美版ppt课件

这是一份人教版 (五四制)八年级上册20.3 等腰三角形完美版ppt课件，文件包含人教版五四学制八上数学2031等腰三角形第2课时教案doc、人教版五四学制八上数学2031等腰三角形第2课时课件pptx等2份课件配套教学资源，其中PPT共15页， 欢迎下载使用。

20.3.1 等腰三角形
第二课时
（1）如图，∵AB=AC∴ = ( )
（2）如图，
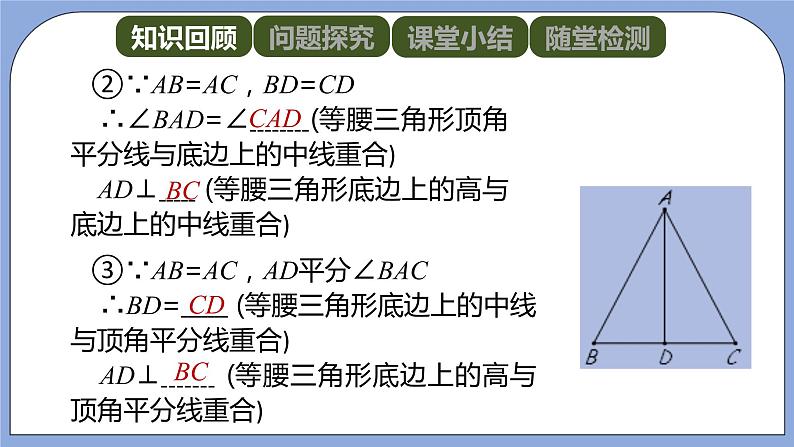
①∵AB=AC，AD⊥BC∴∠BAD=∠ (等腰三角形顶角平分线与底边上的高重合 ) BD= (等腰三角形底边上的中线与底边上的高重合)
∠B
∠C
等边对等角
CAD
CD
②∵AB=AC，BD=CD∴∠BAD=∠ (等腰三角形顶角平分线与底边上的中线重合) AD⊥ (等腰三角形底边上的高与底边上的中线重合)
③∵AB=AC，AD平分∠BAC∴BD= (等腰三角形底边上的中线与顶角平分线重合)AD⊥ (等腰三角形底边上的高与顶角平分线重合)
CAD
BC
CD
BC
活动1
探究一：等腰三角形判定定理的证明
思考
我们知道，如果一个三角形有两条边相等，那么它们所对的角相等.
相等
你能证明你的猜想吗？
反过来，如果有两角相等，那么它们所对的边有什么关系？
活动1
探究一：等腰三角形判定定理的证明
D
证明
AD
AAS
全等三角形的对应边相等
活动2
探究一：等腰三角形判定定理的证明
反思提炼
等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．
注意：
（1）要弄清判定定理的条件和结论，不要与性质定理混淆．
（2）不能说“一个三角形两底角相等，那么两腰边长相等”，因为还未判定它是一个等腰三角形．
（3）判定定理得到的结论是三角形是等腰三角形，性质定理是已知三角形是等腰三角形，得到边和角关系.
活动1
探究二：文字命题的证明方法
重点、难点知识★▲
例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．
【思路点拨】
这个题是文字叙述的证明题，我们首先根据题意画出相应的几何图形，再按图形写出已知（条件转化为已知）、求证（结论转化为求证），最后再证明. 要证AB＝AC，可先证∠B=∠C.
活动1
探究二：文字命题的证明方法
重点、难点知识★▲
证明：∵AD∥BC，∴∠1＝∠B（两直线平行，同位角相等 ） ∠2＝∠C（两直线平行，内错角相等）， 而已知 ∠1＝∠2，∴ ∠B＝∠C .∴AB＝AC（等角对等边）.
例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．
活动2
探究二：文字命题的证明方法
重点、难点知识★▲
集思广益，归纳反思
证明文字命题的一般步骤：
分清命题的条件和结论；根据题意画出正确图形；结合图形写出“已知”、“求证”；分析题意，探索证题思路；依据思路写出证明过程.
活动2
探究二：文字命题的证明方法
重点、难点知识★▲
练习 求证：如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形．
证明：∵CD是边AB上的中线，∴点D是AB的中点 即 AD＝BD
∴AD＝CD，BD＝CD ∴∠1＝∠A，∠2＝∠B
 
 
探究三：等腰三角形的尺规作图
例2 已知等腰三角形底边长为a，底边上的高为h，求作这个等腰三角形.
作法：
作线段AB=a；作线段AB的垂直平分线MN，与AB相交于点D；在MN上取一点C,使DC=h；连接AC、BC;
D
探究三：等腰三角形的尺规作图
练习：如图，已知线段c，求作等腰直角三角形，使其斜边等于线段c．（保留作图痕迹，不必写作法）
知识梳理
（1）等腰三角形的判定方法有两种：一是使用定义（有两边相等的三角形是等腰三角形）；二是使用判定定理（等角对等边）．（2）文字命题的证明步骤.（3）等腰三角形中的尺规作图.
重难点归纳
（1）记清等腰三角形的性质和判定的联系和区别；（2）运用“等边对等角”或“等角对等边”时，要注意是在同一个三角形中使用.（3）证明两条线段相等，常用的方法是证明两条线段所在的三角形全等；若两条线段在同一个三角形中，常用“等角对等边”来证明．
选择“《等腰三角形（2）》随堂检测 ”
点击“随堂训练→名师训练”