陕西省渭南市2023届高三下学期教学质量检测(Ⅱ)理科数学试题（含答案）

渭南市2023年高三教学质量检测（II）

数学试题（理科）

注意事项：

1. 本试题满分150分，考试时间120分钟.

2. 答卷前务必将自己的姓名、学校、班级、准考证号填写在答题卡和答题纸上.

3. 将选择题答案填涂在答题卡上，非选择题按照题号完成在答题纸上的指定区域内.

第I卷（选择题 共60分）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合，，则（    ）

A.        B.         C.         D.

2. 已知平面向量，满足，则向量与的夹角为（    ）

A.        B.        C.         D.

3. 已知为等差数列，其前项和为，若，则（    ）

A. 6         B. 7        C. 8       D. 9

4. 在测量某物理量的过程中，因仪器和观察的误差，使得次测量分别得到，，…，共个数据.我们规定所测量物理量的“最佳近似值”应该满足与所有测量数据的差的平方和最小.由此规定，从这些数据得出的“最佳近似值”应是（    ）

A.         B.         C.        D.

5. 棣莫弗公式（为虚数单位）是由法国数学家棣莫弗（1667-1754）发现的.若复数满足，根据棣莫弗公式可知，复数对应的点在复平面内的（    ）

A. 第一象限        B. 第二象限       C. 第三象限        D. 第四象限

6. 将抛物线绕其顶点顺时针旋转90°之后，正好与抛物线重合，则（     ）

A.      B.        C. -2        D. 2

7. 函数的大致图像为（     ）

A.                     B.

C.                D.

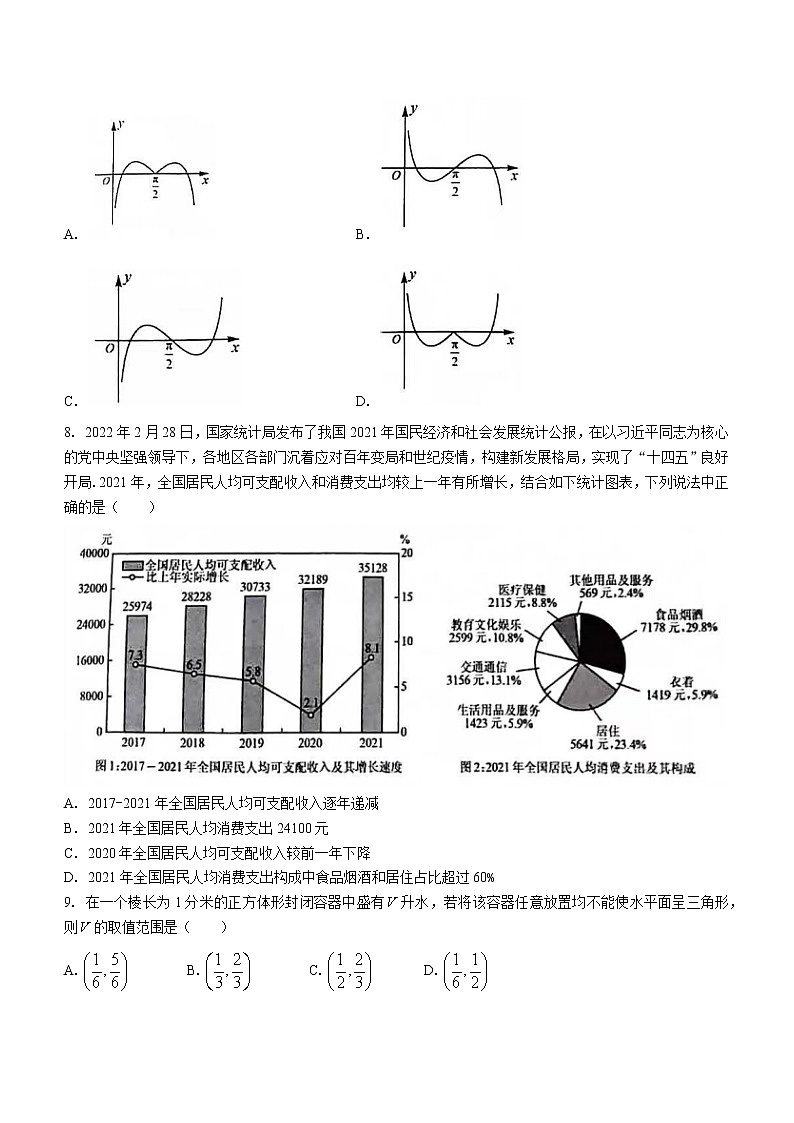
8. 2022年2月28日，国家统计局发布了我国2021年国民经济和社会发展统计公报，在以习近平同志为核心的党中央坚强领导下，各地区各部门沉着应对百年变局和世纪疫情，构建新发展格局，实现了“十四五”良好开局.2021年，全国居民人均可支配收入和消费支出均较上一年有所增长，结合如下统计图表，下列说法中正确的是（    ）

A. 2017-2021年全国居民人均可支配收入逐年递减

B. 2021年全国居民人均消费支出24100元

C. 2020年全国居民人均可支配收入较前一年下降

D. 2021年全国居民人均消费支出构成中食品烟酒和居住占比超过60%

9. 在一个棱长为1分米的正方体形封闭容器中盛有升水，若将该容器任意放置均不能使水平面呈三角形，则的取值范围是（    ）

A.        B.        C.       D.

10. 已知直线过双曲线的左焦点且与的左、右两支分别交于两点，设为坐标原点，为的中点，若是以为底边的等腰三角形，则直线的斜率为（    ）

A.       B.       C.        D.

11. 在正方体中，，为的中点，点在线段（不含端点）上运动，点在棱上运动，为空间中任意一点，则下列结论不正确的是（    ）

A.异面直线与所成角的取值范围是

B. 若，则三棱锥体积的最大值为

C.的最小值为

D.平面

12. 已知函数，将的所有极值点按照由小到大的顺序排列，得到数列，对于，则下列说法中正确的是（    ）

A.                        B.

C. 数列是递增数列          D.

第II卷（非选择题 共90分）

二、填空题：本题共4小题，每小题5分，共20分.

13. 设，且，则的最小值是____________.

14. 写出与圆和圆都相切的一条直线的方程___________.

15. 甲、乙、丙3人去食堂用餐，每个人从这5种菜中任意选用2种，则菜恰有2人选用的情形共有______________种.（用数字作答）

16. 若函数的关系式由方程确定.则下述命题中所有真命题的序号为_____________.

①函数是减函数；           ②函数是奇函数；

③函数的值域为      ④方程无实数根：

⑤函数的图像是轴对称图形.

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.

（一）必考题：共60分.

17.（12分）随着生活水平的不断提高，人们更加关注健康，重视锻炼。通过“小步道”，走出“大健康”，健康步道成为引领健康生活的一道亮丽风景线.如图，为某区的一条健康步道，为线段，是以为直径的半圆，.

（1）求的长度；

（2）为满足市民健康生活需要，提升城市品位，改善人居环境，现计划新建健康步道（在两侧），其中为线段.若，求新建的健康步道的路程最多可比原有健康步道的路程增加多少长度？

18.（12分）在数字通信中，信号是由数字“0”和“1”组成的序列.现连续发射信号次，每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为.

（1）当时，求；

（2）已知切比雪夫不等式：对于任一随机变量，若其数学期望和方差均存在，则对任意正实数，有.根据该不等式可以对事件“”的概率作出下限估计.为了至少有98%的把握使发射信号“1”的频率在0.4与0.6之间，试估计信号发射次数的最小值.

19.（12分）在斜三棱柱（侧棱不垂直于底面中，侧面底面，底面是边长为2的正三角形，.

（1）求证：；

（2）求二面角的正弦值.

20.（12分）在直角坐标系中，已知椭圆的右顶点、下顶点、右焦点分别为.

（1）若直线与椭圆的另一个交点为，求四边形的面积；

（2）设是椭圆上的两个动点，直线与的斜率之积为，若点满足：.问：是否存在两个定点，使得为定值？若存在，求出的坐标；若不存在，请说明理由.

21.（12分）已知函数.

（1）证明：；

（2）若，求实数的取值范围；

（3）证明：.

（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.

22.[选修4-4：坐标系与参数方程]（10分）

在直角坐标系中，曲线的参数方程为（为参数，，），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为.

（1）求曲线的普通方程和直线的直角坐标方程；

（2）已知点，若直线与曲线交于两点，求的值.

23. [选修4-5：不等式选讲]（10分）

已知函数.

（1）当时，求的最小值；

（2）若时，对任意使得不等式恒成立，证明：

.

参考答案

一、选择题

二、填空题

13.

14. 或或三条中任写一条即可.

15. 288

16. ①④⑤

三、解答题

17.解：（1）联结，在中，由余弦定理可得，

，

所以，即的长度为；

（2）记，则在中，由余弦定理可得：

，即，

从而

所以，则，当且仅当时，等号成立；

新建健康步道的最长路程为，

故新建的健康步道的路程最多可比原有健康步道的路程增加

18.解：（1）由已知，

所以

；

（2）由已知，所以，，

若，则，即，

即

由切比雪夫不等式，

要使得至少有98%的把握使发射信号“1”的频率在0.4与0.6之间，则，

解得，所以估计信号发射次数的最小值为1250；

综上，，估计信号发射次数的最小值为1250.

19. （1）证明：

如图，取的中点，连接，

∵，

∴

∵底面是边长为2的正三角形，

∴，

∴，

又，

∴平面，且平面，

∴；

（2）解：法一如图，过点作于点，连接.

∵侧面底面，

∴侧面平面，又，侧面平面，

∴侧面，又平面，

∴，又且，

∴平面，∴，

∴为所求二面角的平面角，

∵，∴，

又，

∴，

∴平面角的正弦值为

法二  

如图，取的中点，以为坐标原点，射线分别为轴的正方向建立空间直角坐标系，则，

∴，

设为平面的法向量，

∴，

令，得

又为平面的一个法向量，

设二面角的大小为，显然为锐角，

，

则，∴二面角的正弦值为.

20.解（1）直线方程为，与椭圆联立可解得，

四边形的面积；

（2）设，由，有，

又在椭圆上，有，

设点，由题意可得，

即

所以点的轨迹在椭圆上，

所以存在两个定点，使得为定值.

21.（1）解：令，，由，解得，

当时，；当时，；

所以在递减，递增，

即，即；

（2）由可得：

由（1）知（当且仅当取等号），

，所以，即；

（3）由（1）知，令，可得，

所以

因为数列是首项为1，公比为的等比数列，

所以.

22. 解（1）曲线的参数方程为（为参数，），

所以，所以.

即曲线的普通方程为

直线的极坐标方程为，则，

转换为直角坐标方程为.

（2）直线过点，直线的参数方程为（为参数），令点对应的参数分别为，

由代入，得，则，，

即为负，

故.

23.解：（1）当时，，

当，，；

当；

当，，；

∴当时，的最小值为2；

（2），当时，

可化为，

令，，，∴，

∴，

当且仅当时取得等号；

又当时，，

故.