辽宁省葫芦岛市兴城市2022届九年级第二次模拟考试数学试卷(含解析)

这是一份辽宁省葫芦岛市兴城市2022届九年级第二次模拟考试数学试卷(含解析)，共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022年辽宁省葫芦岛市兴城市九年级第二次中考模拟
数学试题
一、选择题
1. 下列四个数中，最小的数是（ ）
A. B. C. 0 D. 1
2. 如图是由大小相同的6个正方体搭成的几何体，其主视图是（ ）

A. B.
C. D.
3. 下列运算正确的是（ ）
A. B.
C D.
4. 剪纸艺术是中华民族的瑰宝，下面剪纸作品中，既是轴对称图形又是中心对称图形的是（ ）
A. B.
C. D.
5. 为加强交通安全教育，某班50名学生参加了“交通安全”知识竞赛，测试成绩如下表，其中两个数据被遮盖．
成绩（分）
86
88
90
92
94
95
96
98
99
100
人数（人）
■
1
■
1
4
5
6
5
8
7
下列关于成绩的统计量中，与被遮盖的数据无关的是（ ）
A. 平均数 B. 众数 C. 中位数 D. 方差
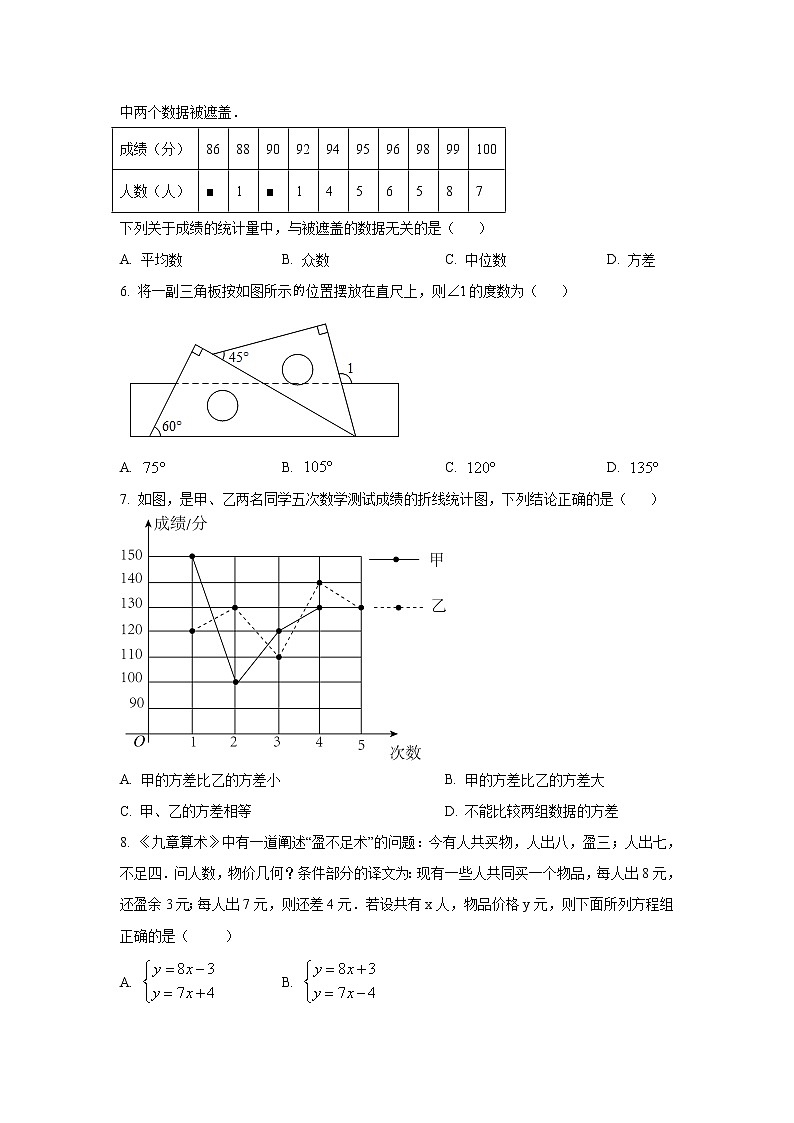
6. 将一副三角板按如图所示位置摆放在直尺上，则的度数为（ ）

A. B. C. D.
7. 如图，是甲、乙两名同学五次数学测试成绩的折线统计图，下列结论正确的是（ ）

A. 甲的方差比乙的方差小 B. 甲的方差比乙的方差大
C. 甲、乙的方差相等 D. 不能比较两组数据的方差
8. 《九章算术》中有一道阐述“盈不足术”的问题：今有人共买物，人出八，盈三；人出七，不足四．问人数，物价几何？条件部分的译文为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元．若设共有x人，物品价格y元，则下面所列方程组正确的是（ ）
A. B.
C. D.
9. 如图，平面直角坐标系中，以为直径的与x轴交于点C，连接交y轴交于点，反比例函数的图象经过点B，则k的值为（ ）

A B. C. D. 1
10. 如图，中，，点D从点A出发，以每秒1个单位的速度沿线段作匀速运动，同时点E从点B出发，沿射线以每秒个单位的速度作匀速运动，当点D与点B重合时两点停止运动，连接．设点D运动的时间为x秒，的面积为y，则下列图象中能表示y与x的函数关系的图象大致是（ ）

A. B.
C. D.
二、填空题
11. 冠状病毒是一大类病毒的总称．在电子显微镜下可以观察到它们的表面有类似日冕状突起，看起来像王冠一样，因此被命名为冠状病毒，其平均半径大约为0.00000005m；将0.00000005用科学记数法表示为______．
12. 分解因式：_________．
13. 不等式组的解集是_____．
14. 将直线向上平移3个单位长度，平移后的直线与y轴的交点坐标为_________．
15. 如图，正方形中，对角线和相交于点O，点E在线段上，交于点F，小明向正方形内投拥一枚飞镖，则飞镖落在阴影部分的概率是_________．

16. 如图，平面直角坐标系中，点，点，以A为圆心，为半径作弧交x轴于点C，连接，分别以A，C为圆心，大于长为半径作弧，两弧交于点D，直线交于点E，连接，则线段的长为_________．

17. 如图，在每个小正方形的边长均为1的网格图中，一段圆弧经过格点A，B，C，格点C，D的连线交于点E，则的长为_____________．

18. 如图，正方形中，点E，F，G分别是的中点，与交于点H，与交于点N，连接，则下列结论：①四边形是平行四边形；②；③；④；⑤．其中正确结论的序号是_____________．

三、解答题
19. 先化简，再求值： ，其中x=+tan45°
20. 某校以“我最喜爱的冰雪运动”为主题对全校学生进行随机抽样调查，调查的运动项目有短道速滑，花样滑冰，速度滑冰，冰壶以及其他项目（每个同学必须选择且只能选择一个项目），并根据调查结果绘制出如图所示的两幅不完整的统计图：

（1）本次调查共抽取了多少名同学？
（2）将条形统计图补充完整；
（3）如果该校有1200名学生，请估计最喜欢冰壶的有多少人？
（4）在学校举办的“共筑冰雪中国梦”的主题演讲比赛中，小明获得了一等奖，他可以在包装完全相同的A，B，C，D四枚冬奥纪念章中选取两枚，请用列表或画树状图法求出小明选到的纪念章恰好是“A”和“C”图案的概率．

21. 某商场计划购进一批甲、乙两种消毒液，已知甲种消毒液一瓶进价与乙种消毒液一瓶的进价的和为40元，用90元购进甲种消毒液的瓶数与用150元购进乙种消毒液的瓶数相同．
（1）求甲、乙两种消毒液每瓶的进价分别是多少元？
（2）若购买甲、乙两种消毒液共50瓶，且总费用不超过1000元，求甲种消毒液至少要购买多少瓶？
22. 在某次数学实践活动课中，甲、乙、丙三个学习小组对校园中一些设施进行了测量，获得如下信息：
甲组：领操台的高为，宽为．
乙组：与地面平行
丙组：在C点测得旗杆底端B的俯角为，在D点测得旗杆顶端A点的仰角为．
（图中各点均在同一平面内）

（1）求领操台到旗杆的距离的长；
（2）求旗杆的高度．（结果精确到，参考数据：）
23. 某批发商以6元/千克的进价购进某种蔬菜，销往零售超市，批发商销售过程中发现，这种蔬菜的销售单价为10元/千克时，每天的销售量为300千克，如果调整价格，销售单价每涨1元，每天少卖出30千克，设销售价格为元/千克，每天的销售量为千克．
（1）请直接写出与之间的函数关系式；
（2）当每天销售单价是多少元时，该批发商销售这种蔬菜的利润为1440元？
（3）端午节期间，批发商对这种蔬菜进行优惠促销，每购买1千克这种蔬菜，赠送成本为2元的端午节饰品，这种蔬菜的售价定为多少元时，该批发商每天的销售利润最大，最大利润是多少元？
24. 如图，为的直径，点C和点D是上的两点，连接，交的延长线于点E．

（1）求证：是的切线；
（2）若，求的长．
25. 在平行四边形中，，，平分交线段于点，在□的外部作，使，，连接，，线段与交于点．

（1）当时，请直接写出线段和的数量关系；
（2）当时，
①请写出线段，，之间的数量关系，并说明理由；
②若点是的三等分点，请直接写出的值．
26. 已知抛物线与x轴交于点和点，与y轴交于点C，点D在抛物线上运动（不与点A，B，C重合）．

（1）求抛物线的解析式；
（2）如图1，当点D在第一象限抛物线上运动时，过点D作轴，垂足为点F，直线与直线交于点E，若，求点D的坐标；
（3）如图2，直线交直线于点H，点G在坐标平面内，在抛物线上是否存在点D，使以点A，D，H，G为顶点的四边形为矩形，若存在，请直接写出点D的坐标；若不存在，请说明理由．
答案

1. B
解：∵-|-3|=-3，
∴＜＜0＜1，
∴其中最小的数．
故选：B．
2. A
解：从正面看有2层，底层是3个小正方形，上层有2个小正方形，
所以主视图是：

故A符合题意， 故选：A．
3. A
，故A计算正确，符合题意；
，故B计算错误，不符合题意；
，故C计算错误，不符合题意；
，故D计算错误，不符合题意．
故选A．
4. D
∵ 选项A是轴对称图形，
∴不符合题意；
∵选项B不是轴对称图形，也不是中心对称图形
∴不符合题意；
∵选项C不是轴对称图形，也不是中心对称图形，
∴不符合题意；
∵选项D是轴对称图形，也是中心对称图形，
∴符合题意；
故选D．
5. C
解：根据题意可知与被遮盖的数据无关是中位数，
故选C．
6. B
解：如图，
∵，
，
∴，
∵，
∴．
故选：B．

7. B
解：从图中可以看出：甲组数据的折线统计图起伏较大，所以甲组的数据不如乙组的数据稳定．
故选：B．
8. A
解：设共有x人，物品价格y元，根据题意可列方程组：
，
故选A.
9. A
解：连接AC，过点B作轴于点E，
，
∴OD=1，
在中，AB是直径，

，
，
又 OA=OC，
是等边三角形，
，
在中，DC=2OD=2，
，
，
，
在中，，
，，
点B的坐标为，
∵反比例函数的图象经过点B，
，
故选：A．

10. C
解：如图，设BC交DE于点P，过点D作DQ⊥BC于点Q，则∠BQD=90°，

根据题意得：，则，
∵，
∴∠ABC=45°，，
∴△BDQ是等腰直角三角形，
∴，
∵BF⊥BC，
∴BF∥DQ，
∴△BEP∽△QDP，
∴，即，
解得：，
∴，
∴，
∵，
∴该函数图象为位于y轴以及右侧的抛物线的一段．
故选：C
11.
解：，
故答案为：．
12.
解：
故答案为: ．
13. ＜x≤
解： ,
由①得2x+5>0，
x＞-，
由②得4x-9≤0,
x≤，
故不等式组的解集为＜x≤．
14. （0，4）
解：∵直线y=2x+1沿y轴向上平移3个单位，
∴平移后的解析式为：y=2x+1+3=2x+4，
当x=0，则y=4，
∴平移后直线与y轴的交点坐标为：（0，4）．
故答案为：（0，4）．
15.
解：ABCD是正方形，则OD=OC，∠ODF=∠OCE=45°，∠COD=90°，
∠EOF=∠COD，则∠EOF-∠FOC=∠COD-∠FOC，
∴∠EOC=∠FOD，
∴△OCE≌△ODF（ASA），
∴△OCE面积等于△ODF面积，
∴阴影面积=△ODC面积=正方形面积，
∴飞镖落在阴影部分的概率是，
故答案为：；
16. 1
解：∵点，点，
∴AB=1+1=2，OA=OB，
∵AB=AC，
∴，
∴，
∴∠BAC=60°，
∴△ABC是等边三角形，
由题意得BD垂直平分线段AC，
∴AE=CE，
∴，
故答案为：1．
17.
解：如图所示：连接、、，
∵，
∴是直径，
∴，
根据网格图形可知：
， ，
∴，
∴是等腰直角三角形，
∴，，
∴，
∴所对的圆心角是90°，
∴的长为以为直径的圆周长的，
即．
故答案为：．

18. ①②④
解：∵四边形ABCD是正方形，
∴AD=BC=AB=CD，∠ABG=∠ADC=90°，
∵点E，G分别是AD、BC的中点，
∴AE=BG，
∴△ABG≌△CDE（SAS），
∴AG=CE，
∴四边形是平行四边形，故①正确；
同理可证△ABG≌△BCF≌△CDE，
∴∠BAG=∠CBF=∠DCE，∠AGB=∠BFC=∠CED，
∵∠BAG+∠AGB=90°，
∴∠CBF+∠AGB=∠BFC+∠DCE=90°，
∴∠BNG=∠BHC=90°，
∴NG∥CH，
∵点G是BC的中点，
∴，
∴，故②正确；
∵∠BAN=∠CBH，AB=BC，∠ANB=∠BHC=90°，
∴△ABN≌△BCH，
∴AN=BH=2NH，
∴tan∠AHN=，
∴∠AHN60°，故③错误；
∵GH=BG，GN⊥BH，
∴∠BGN=∠HGN，
又∵AG=AG，
∴△ABG≌△AHG，
∴AH=AB=CD，
∵CD2+DE2=CE2，
∴，故④正确；
设CF=1，则BC=2，
∴，
∴，
∴，EH=CE-HC=，
过点H作HM⊥AD于M，则△EHM∽△EDC，
∴，
∴，
∴，，
∴DM=DE-EM=，
∴，
∴，故⑤错误；
故答案为：①②④．


19. 解：



∵x=+tan45°=4+1=5，
∴原式=．
20. （1）
30÷25%=120人
答：本次调查共抽取了120名同学．
（2）
速度滑冰的人数为：120－24－30－18－12=36人
补全条形统计图如图所示：

（3）
1200×=180人
答：估计最喜欢冰壶的有180人．
（4）

A
B
C
D
A

（B ，A）
（C ，A）
（D， A）
B
（A ，B）

（C ，B）
（D， B）
C
（A ，C）
（B ，C）

（D ，C）
D
（A ，D）
（B ，D）
（C， D）


一共产生12种结果，每种结果发生的可能性相同，其中恰好选中A和C的结果有2种，分别是（A，C），（C，A），
∴P（恰好选中A和C）=．
21. （1）
解：设甲种消毒液每瓶的进价为x元，则乙种消毒液每瓶的进价为元．
根据题意，得：，解得．
检验：当时，，
∴是原分式方程的解，且符合题意，
∴．
∴甲种消毒液每瓶的进价为15元，乙种消毒液每瓶的进价为25元．
（2）
解：设购买甲种消毒液m瓶，则购买乙种消毒液瓶．
根据题意，得：，解得．
∴甲种消毒液至少要购买25瓶．
22. （1）
延长DC交AB于点G，
由题可知∠GCE=∠CEB=∠GBE=90º，
∴四边形BECG是矩形，
∴BE=GC，BG=CE=1.6
在Rt△BGC中，∠BCG=22°，
∴BE=GC=BG÷tan22º≈1.6÷0.4≈4.0
答：领操台到旗杆的距离BE的长约为4.0米；

（2）
∵GC=4，CD=2.5，
∴GD=GC+CD=6.5，
在Rt△ADG中，∠ADG=60º，
∴AG=GD·tan∠ADG=6.5×≈11.05，
∴AB=AG+GB=11.05+1.6≈12.7，
答：旗杆AB的高度约为12.7米．
23. （1）
解：．
∴与之间的函数关系式为：．
（2）
设批发商销售这种蔬菜每天的利润为元，
∵利润＝销售量×（销售单价－进价），
∴，
当时，得：
，
整理方程得：，
解得：，，
答：当每天销售单价是14元或12元时，该批发商销售这种蔬菜的利润为1440元．
（3）
设每天获得利润元，
∵端午节期间，批发商对这种蔬菜进行优惠促销，每购买1千克这种蔬菜，赠送成本为2元的端午节饰品，
∴每千克的利润为元，
∴
，
∵，
∴抛物线开口向下，
∴当时，有最大值，．
答：这种蔬菜的零售价是14元时，每天可获得最大利润，最大利润为1080元．
24. （1）
证明：连接OD，OC，
∵OD=OB，OC=OC，BC=CD
∴△COD≌△COB
∴∠OCD=∠BCO
∵CO=BO
∴∠B=∠BCO
∵∠B=∠ADC
∴∠ADC=∠DCO
∴DA//CO
∴∠E+∠ECO=180º
∵CE⊥EA
∴∠E=90º
∴∠ECO=90º
∴EC⊥CO
∵CO是⊙O的半径
∴EC是⊙O切线

（2）
解：连接AC
由（1）可知∠ECA+∠ACO=90º
∵AB是⊙O的直径
∴∠ACB=90º
∴∠ACO+∠OCB=90º
∴∠ECA=∠OCB
∵OC=OB
∴∠B=∠OCB
∴∠ECA=∠B
∵∠B=∠ADC
∴∠ADC=∠ECA
∵∠E=∠E
∴△EAC∽△ECD
∴
∵AE=2，CE=4
∴ED=8，
∴AD=6
25. （1）
解：线段和的数量关系∶，理由如下：
如图，连接，
∵四边形是平行四边形，，
∴，，，
，
∵平分，
∴，
∴，
∴，
∴，
∴，
∵，，
∴是等边三角形，
∴，
∴，
，
∴，
在和中，

∴，
∴，，
∴


，
∴是等边三角形，
∴．

（2）
①如图，连接，
∵四边形是平行四边形，，
∴四边形是矩形，
∴，，，，
∵平分，
∴，
∴，
∴，
∴，
∴，
∵，，
∴，
∴，
，
，
∴，
在和中，

∴，
∴，，
∴


，
∴，
∵在中，
∴，
∴．
②点是的三等分点，
分两种情况：
第一种情况：，设，
由①可知：在中，，，
∴，
∴，，
∴
由①可知：在中，，，
∴，
，
∴，
∵，
∴，
∴，
∴，
∵，
∴，，
∴，
∴，
∴，
∴，
∴，
由①可知：在中，，
∴，
∴，
∵，
∴，
∴；
第二种情况：，设，
由①可知：在中，，，
∴，
∴，，
∴
由①可知：在中，，，
∴，
，
∴，
∵，
∴，
∴，
∴，
∵，
∴，，
∴，
∴，
∴，
∴，
∴，
由①可知：在中，，
∴，
∴，
∵，
∴，
∴．
∴的值为或．

26. （1）
解：∵抛物线y=－x2+bx+c经过点A（3，0）和点B（-1，0），
∴，
∴，
∴y=-x2+2x+3．
（2）
∵y=-x2+2x+3，
∴当x=0时，y=3，
∴点C（0，3），
∵A（3，0），
∴设AC的解析式为y=kx+b1，
∴
∴，
∴AC的解析式为y=-x+3，
设点D（m，-m2+2m+3），
∴E（m，-m+3），
∴DE=（-m2+2m+3）-（3﹣m）=-m2+3m，
∴EF=-m+3，
∵A（3，0），C（0，3），
∴AO=CO，
∴∠CAO=45º，
∴AE=EF÷sin45º=（3-m），
∵DE=AE，
∴－m2+3m=（3-m），
∴m1=，m2=3（不合题意，舍去）
把m1=代入y=-x2+2x+3得：y=-（）2﹢2+3=2+1
∴点D坐标为（，2+1）．

（3）
存在；设点D的坐标为：；
当BD⊥AC，AD为对角线时，过点D作DF⊥x轴于点F，交AC于点E，如图1所示：
根据解析（2）可知，，
∴∠AEF=90°-45°=45°，
∴∠DEH=∠AEF=45°，
∵∠DHE=90°，
∴∠HDE=90°-45°=45°，
∴，
∴，
∴，
即，
解得：或（舍去），
∴，
∴此时点D的坐标为：（2，3）；
当AD⊥AC，AD为矩形的一条边时，过点D作DM⊥x轴于点M，如图2所示：
∵，∠DAC=90°，
∴∠DAB=90°-45°=45°，
∵∠DMA=90°，
∴∠MDA=90°-45°=45°，
∴∠MDA=∠MAD，
∴MD=MA，
即，
解得：，（舍去），
∴，
∴此时点D的坐标为：（-2，-5）；
当AD⊥DH，AD为一条边时，过点D作DM⊥x轴于点M，如图3所示：
，
∴，，
∴，
∴，
∴，
即，
，
，
解得：，，
把，和分别代入得：，
∴点D的坐标为（1+，1）或（1-，1）；
综上分析可知，点D的坐标为：（2，3），（1+，1），（1-，1），（-2，-5）．