辽宁省葫芦岛市连山区2022届九年级中考模拟测试（二）数学试卷(含解析)

这是一份辽宁省葫芦岛市连山区2022届九年级中考模拟测试（二）数学试卷(含解析)，共28页。试卷主要包含了选择题，四象限，则一次函数的图象大致是，解答题等内容，欢迎下载使用。

2022年葫芦岛市连山区初中毕业生模拟考试二
数学试卷
※考试时间120分钟 满分150分
第一部分 选择题（共30分）
一、选择题（本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 下列各式，结果为﹣3的是（ ）
A. ﹣（﹣3） B. ﹣|3|
C. ＋|﹣3| D. |﹣（＋3）|
2. 下列计算正确的是（ ）
A. B.
C. D.
3. 甲、乙、丙、丁四名同学进行体温测量，他们5天的平均体温都是36.5度，方差分别是＝0.02，＝0.04，＝0.06，＝0.08，则体温最稳定的是（　　）
A. 甲 B. 乙 C. 丙 D. 丁
4. 如图，立体图形俯视图是( )

A. B.
C. D.
5. 某校举办主题为“关爱身心健康，致敬可爱守护者”的演讲比赛，进入决赛的6名选手的成绩（单位：分）分别为：9.0，8.4，9.2，8.5，9.2，9.5，则这组数据的中位数和众数分别是（ ）
A. 9.1，9.2 B. 9.1，9.5 C. 9.0，9.2 D. 8.5，9.5
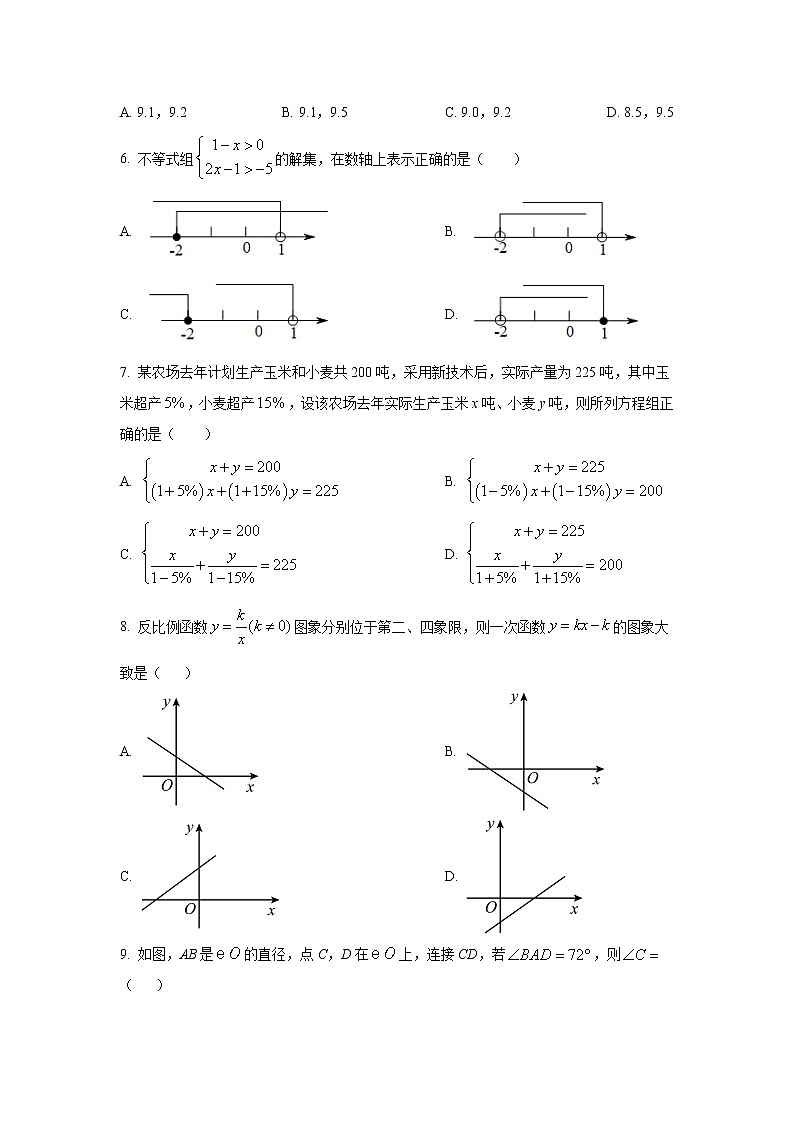
6. 不等式组的解集，在数轴上表示正确的是（　　）
A. B.
C. D.
7. 某农场去年计划生产玉米和小麦共200吨，采用新技术后，实际产量为225吨，其中玉米超产，小麦超产，设该农场去年实际生产玉米x吨、小麦y吨，则所列方程组正确的是（ ）
A. B.
C. D.
8. 反比例函数图象分别位于第二、四象限，则一次函数的图象大致是（ ）
A. B.
C. D.
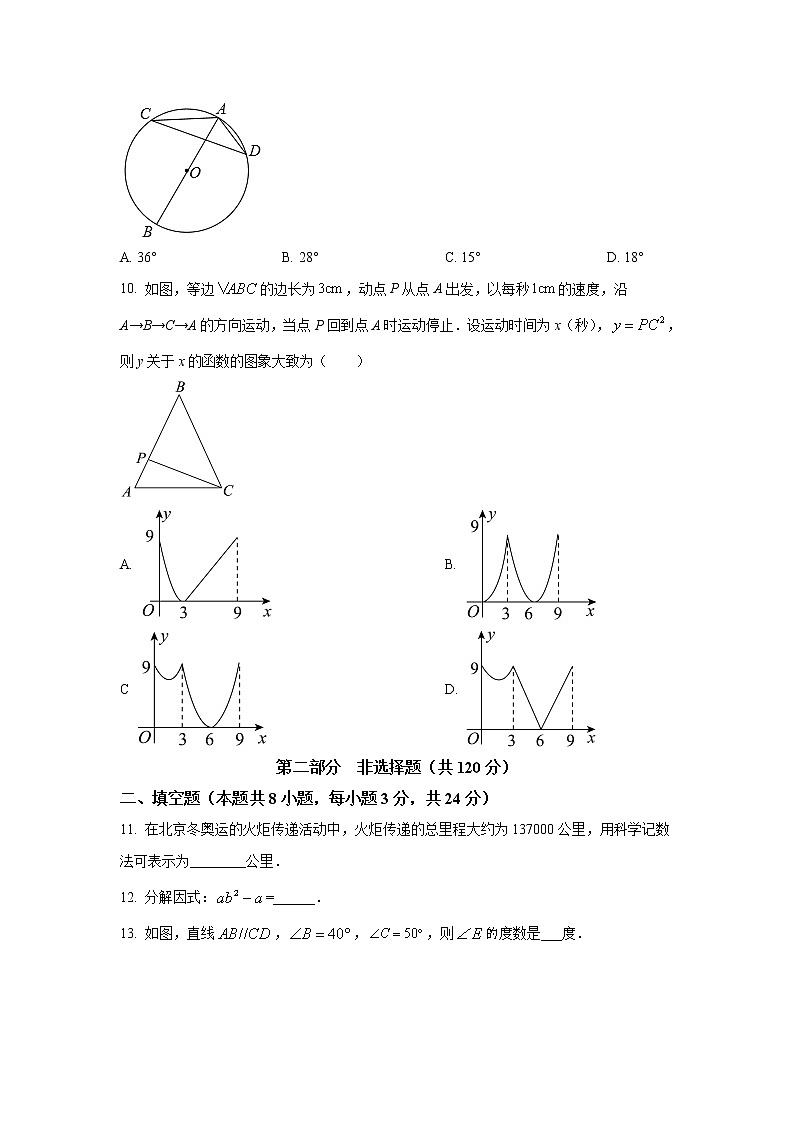
9. 如图，AB是的直径，点C，D在上，连接CD，若，则（ ）

A. 36° B. 28° C. 15° D. 18°
10. 如图，等边的边长为，动点P从点A出发，以每秒的速度，沿A→B→C→A的方向运动，当点P回到点A时运动停止．设运动时间为x（秒），，则y关于x的函数的图象大致为（ ）

A. B.
C D.
第二部分 非选择题（共120分）
二、填空题（本题共8小题，每小题3分，共24分）
11. 在北京冬奥运的火炬传递活动中，火炬传递的总里程大约为137000公里，用科学记数法可表示为________公里．
12. 分解因式：=______．
13. 如图，直线，，，则度数是___度．

14. 若关于的方程有两个不相等的实数根，则的取值范围是_____．
15. 如图，正方形是一飞镖游戏板，其中点，，，分别是各边中点，并将该游戏板划分成如图中所示的9个区域，现随机向正方形内投掷一枚飞镖（投中各区域的边界线或没有投中游戏板，则重投1次），则投中阴影区域的概率是______．

16. 如图，在平面直角坐标系中，点，点B在y轴正半轴上，以AB为一边向直线AB斜下方作正方形ABCD．且正方形边长为5，若双曲经过点D，则k的值为_________．

17. 如图，点E是斜边AC上一点，，将沿BE翻折，得到，再在AC边上取点F，使点C关于BF的对称点恰好落在上，连接，当是直角三角形时，AE的长是_______．

18. 如图，直线AM的解析式为与x轴交于点M，与y轴交于点A，以OA为边作正方形ABCO，过点B作交MH于点，交x轴于点，过点作x轴的垂线交MA于点，连接；以为边作正方形，过点作交MA于，交x轴于点，过点作x轴的垂线交MA于点，连接；以为边作正方形，则的长为_________．

三、解答题（19题10分，20题12分，共22分）
19. 先化简，再求代数式的值，其中．
20. 为丰富课后服务内容，某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查，分别用A、B、C、D代表这四门学科，并对调查结果分析后绘制了如下两幅图不完整的统计图．

请你根据图中提供的信息完成下列问题：
（1）求被调查学生的人数？
（2）并将条形统计图补充完整；
（3）已知该校有1500名学生，估计该校学生喜爱学科C的学生有多少人？
（4）小明和小亮参加校本课程学习，若每人从A、B、C三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．
四、解答题（21题12分，22题12分，共24分）
21. 某超市预测某饮料有发展前途，用1200元购进一批饮料，面市后果然供不应求，又用7200元购进这批饮料，第二批饮料的数量是第一批的5倍，但单价比第一批贵2元．
（1）第一批饮料进货单价多少元？
（2）若二次购进饮料按同一价格销售，两批全部售完后，获利不少于2400元，那么销售单价至少为多少元？
22. 如图①是某中型挖掘机，该挖掘机是由基座、主臂和伸展臂构成，图②是其侧面结构示意图（MN是基座，AB是主臂，BC是伸展臂），若主臂AB长为4米，主臂伸展角的范围是：，伸展臂伸展角的范围是：．

（1）如图③，当，伸展臂BC恰好垂直并接触地面时，求伸展臂BC的长（结果保留根号）；
（2）若（1）中BC长度不变，当时，求该挖掘机最远（即伸展臂伸展角最大时）能挖掘到距A水平正前方多少米的土石，（结果保留根号）
五、解答题（本题12分）
23. 某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量（千克）与每千克售价（元）满足一次函数关系，其部分对应数据如下表所示：
每千克售价（元）
…
25
30
35
…
日销售量（千克）
…
102
92
82
…
（1）求与之间的函数表达式；
（2）该超市要想获得1280元的日销售利润，每千克樱桃的售价应定为多少元？
（3）当每千克樱桃售价定为______元时，日销售利润最大，最大利润是______元．
六、解答题（本题12分）
24. 如图，Rt△ABC，∠ABC=90°，点O在AB上，AD⊥CO交CO延长线于点D，∠DAO=∠ACO，以点O为圆心，OB为半径作圆．

（1）求证：AC是⊙O的切线；
（2）已知，求OC的长？
七、解答题（本题12分）
25. 已知：菱形ABCD，，点E菱形对角线BD所在直线上任意一点（不与点B，D重合），连接EC将射线EC绕点E逆时针旋转，与直线AD交于点F．

（1）如图1，当点E在线段BD上时，请直接写出三条线段DE，DC，DF之间的数量关系；
（2）如图2，当点E在线段DB的延长线上时，（1）中结论是否仍然成立，若成立？请说明理出；若不成立？请写出正确的结论，并说明理由；
（3）当时，直接写出的值．
八、解答题（本题14分）
26. 如图1，在平面直角坐标系中，抛物线与x轴交于，与y轴交于点．

（1）求抛物线的解析式；
（2）如图1，在直线BC上方的抛物线上有动点P，过点P作轴，交BC于点Q，当时，求点P的坐标；
（3）如图2，若点D坐标为，轴交直线BC于点E，将沿直线BC平移得到，移动过程中，在坐标平面内是否存在点P，使以点A，C，，P为顶点的四边形为矩形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
答案

1. B
解：A、-（-3）＝3，故A错误；
B、﹣|3|＝-3，故B正确；
C、+|﹣3|＝3，故C错误；
D、|﹣（+3）|＝3，故D错误．
故选B．
2. D
解：A．，选项错误，不符合题意；
B．，选项错误，不符合题意；
C．，选项错误，不符合题意；
D．，选项正确，符合题意；
故选： D．
3. A
解：他们5天的平均体温都是36.5度，方差分别是＝0.02，＝0.04，＝0.06，＝0.08，
．
甲体温最稳定．
故选A
4. C
A、是该几何体的主视图；
B、不是该几何体的三视图；
C、是该几何体的俯视图；
D、是该几何体的左视图．
故选C．
5. A
解：将6名选手的成绩（单位：分）按照从小到大排列是：8.4，8.5，9.0，9.2，9.2，9.5，
故这组数据的众数是9.2，中位数是（9.0+9.2）÷2=9.1，
故选：A．
6. B
解：① ，
移项得： ，
系数化为1得： ；
②，
移项合并同类项得： ，
系数化为1得： ，
∴不等式组的解集为： ．
则在数轴上表示为：

故选B．
7. D
解：∵玉米超产 5% ，小麦超产 15% ，该农场去年实际生产玉米x吨、小麦y吨，
∴该农场原计划生产玉米，小麦，
∵农场去年计划生产玉米和小麦共200吨，
∴，
∵x+y=225，
∴所列方程组为：
，
故选：D．
8. A
解：∵反比例函数图象分别位于第二、四象限，
∴，
∴，
∴一次函数的图象经过第一、二、四象限．
故选：A
9. D
解：如图，连接BD，

AB是的直径，
，
，
，
和同是弧AD所对的圆周角，
，
故选D．
10. C
解：如图，过C作CD⊥AB于点D，
则cm，cm，
当点P在AB上时，，cm，cm，
∴，
该函数图象是开口向上的抛物线，对称轴为直线；
当时，即点P在线段BC上时，cm；
则，
∴该函数的图象是在上的抛物线，且对称轴为；
当 时，即点P在线段CA上，此时，cm，
则，
∴该函数的图象是在上的抛物线，且对称轴为直线；
故选：C．

11.
解：．
故答案为：．
12. a（b+1）（b﹣1）
解：原式==a（b+1）（b﹣1），
故答案为a（b+1）（b﹣1）．
13. 90
解：如图，

∵，，
∴，
∵，，
∴；
故答案为90．
14.
根据题意得，
解得．
故答案为．
15.
解：阴影部分组合起来的面积就等于三角形ABF的面积，
设正方形ABCD的边长是，则，
∵F是BC中点，
∴，
∴，
概率是．
故答案是：．
16. 2
解：如图，分别过点作轴的平行线，交过点平行于轴的平行线于点，过点作轴于点，

，正方形边长为5，
，，
中，，
则，
，
四边形是正方形，
则，，
，
，
，
，
在上，设，
，，，
则，
，
正方形的对角线互相平分，
的中点坐标重合，
即，
解得．
故答案：．
17. 或
在中，．
由轴对称的性质，可得，
∴．
①当时，点在AC上，如解图1所示，
则，
解得，
②当时，如解图2所示，
则，
解得，
综上所述，AE的长是或．

故答案为：或．
18.
如图，分别过点B，B1作A1O1，A2O2的垂线，交A1O1于点F，A2O2于点F1．
由题干易得AO=MO=AB=BC=1，∠AMO=∠EO1M=∠E1O2M=45°，由垂直可得：BC=CO1=O1F=1
∴A1O1=MO1=3且A1O1=3AO
同理可推出A2O2= MO2=9=3A1O1=32
由此可以推出一般形式：An On=3An-1O n-1=3n
∴，，
又∵BF=AO=1，B1F1=A1O1=3，B n-1F n-1=A n-1O n-1=3n-1
∴
∴
故答案为：．

19. 解：原式＝
=
=
=
当x＝3tan30°+2＝3×=，
原式＝ ．
20.（1）解：（人），
答：被调查学生的人数为120人．
（2）
解：A学科人数为（人），
补全图形如下：

（3）
解：（人）
答：估计该校学生喜爱学科C的约有225人．
（4）
解：列表如下：

A
B
C
A



B



C



由列表可知：共有9种等可能的结果，其中两人恰好选中同一门校本课程的结果有3种，
所以两人恰好选中同一门校本课程的概率为．
答：两人恰好选中同一门校本课程的概率为．
21. （1）
解：设第一批饮料进货单价x元，则第二批的单价为(x＋2)元，
依题意得
解得x＝10，
经检验，x＝10是原方程的解，
故第一批饮料进货单价为10元．
（2）
解：第一次购买＝120件，第二次购买件.
设售价为m元，
则120（m－10）＋600(m－12)≥2400，
解得m≥15，
故销售单价至少为15元．
22. （1）
如图：

由题意得：米，

（米）．
（2）
如图：

由题意得，时，伸展臂伸展的最远，
过点B作交NM的延长线于D，
在中，，
，
，

，

在中，，，
，
（米）．
23. 解：（1）设y＝kx+b，
将（25，102）、（30，92）代入，由题意得：
解得：
所以与之间的函数表达式为．
（2）根据题意得：
解得：，
∵
∴（不合题意，应舍去）
∴
答：每千克樱桃的售价应定为36元．
（3）设超市日销售利润为w元，
w＝（x﹣20）（﹣2x+152），
＝﹣2x2+192x﹣3040，
＝﹣2（x﹣48）2+1568，
∵﹣2＜0，
∴当20≤x≤40时，w随x的增大而增大，
∴当x＝40时，w取得最大值为：w＝﹣2（40﹣48）2+1568＝1440，
故答案为：当每千克樱桃的售价定为40元时日销售利润最大，最大利润是1440元．
24. （1）
证明：作OE⊥AC，垂足为E，
∵AD⊥CO，
∴∠ADO=90°，
∴∠ADO=∠ABC=90°，
∵∠AOD=∠BOC，
∴∠DAO=∠BCO，
∵∠DAO=∠ACO，
∴∠BCO=∠ACO，
∵OB⊥BC，OE⊥AC，
∵OE=OB，
∵OB是半径，
∴AC是⊙O的切线；

（2）
解：∵OBC=∠OEC，∠BCO=∠ACO，OC=CO，
∴△OBC≌△OEC，
∴BC=EC=6，
在Rt△ABC中，，
∴AE=AC−EC=10−6=4，
在Rt△AOE中，设半径为R，
∵AE2+OE2=OA2，
∴42+R2=(8−R)2，
∴R=OC=3，
∴在Rt△OBC中，．
25. （1）
连接FC，
由旋转知，∠CEF=60°，EC=EF，
∴△CEF是等边三角形，
在菱形ABCD中，CB=CD，
∠BCD=∠BAD=60°，
∴△CBD是等边三角形，
∴∠FCD+∠DCE=∠DCE+∠BCE=60°，
∴∠DCF=∠BCE，
∴△CDF≌△CBE，
∴BE=DF，
DC=BD=DE+BE=DE+DF，
即DC=DE+DF，
故答案为DC=DE+DF；

（2）
（1）中结论不成立，正确结论为
过点E作，交DC的延长线于点G，

∵四边形ABCD是菱形，

，
和都为等边三角形

，
为等边三角形，
，
，
即


又
,

，
,
即
（3）
设BD=3a，则DE=a，
①当点E在线段BD上时，

∵△BCD和△CEF是等边三角形，
∴CD=CB，CE=CF，∠DCF+∠DCE=∠DCE+∠ECB=60°，
∴∠FCD=∠ECB，
∴△CDF≌△CBE，
∴DF=BE=2a，
过点E作EG⊥BC于G，
在直角△EBG中，∠EBG=60°，
∴BG=BE·cos∠EBG=a，
EG=BE·sin∠EBG= ，
CG=BC-BG=2a，
∴EC= ，
∴ ；
②当点E在BD的延长线上时，
过点F作FG⊥CD于G，
用①的方法得到DF=BE=4a，
在直角△FDG中，
DG=2a，FG= ,
∴GC=DC-DG=a，
在直角三角形FCG中，
FC=，
即EC= ，
∴ ；

故答案为或．
26. （1）将代入，
，
，
；
（2）
设直线BC的解析式为，将代入得
，
解得，
，
设，则，
，
过点Q作轴交于点E，如图：

，

，
，
，
（舍），
；
（3）
存在，；
理由分析:∵ 点D坐标为，B(3,0) ，
∴DB=1,
将直线BC向左平移1个单位即可得到D点运动轨迹所在的直线，
由平移得D点在平移过程中所在直线的解析式为；
∵当时，
，
∴，
∵，
∴，AC的中点坐标为M，
当AC为对角线时，如图1和图2，设D'（n，-n+2），
∵，
∴，
∴，
∴D'（1，1）或D'（-1，3），
由矩形的性质可知，PD'经过点M且被M点平分，
∴，
∴当D'（1，1）时，，即，
当D'（-1，3）时，，即；
当AC为边时，有如下两种情况，如图3和图4，
设D'（n，-n+2），
∵（图3），（图4），
∴（图3），（图4），
∴（图3），（图4），
∴图3中，，图4中，
∴图3中，CD'的中点，图4中，AD'的中点；
所以图3中，，图4中，，
∴图3中，，即，图4中，，即；
综上可得：存在，．