2023年中考数学二轮专题练习-一次函数与反比例函数的实际应用

2023年中考数学二轮专题练习-一次函数与反比例函数的实际应用

一、解答题

1．如图，已知一次函数y1=kx+b的图像与反比例函数y2=图像交于点A(4，1)和点B(a，−2)．

(1)求一次函数与反比例函数的解析式；

(2)当时，直接写出自变量x的取值范围；

(3)如果在x轴上找一点C使△ABC的面积为8，求点C坐标．

2．已知在平面直角坐标系中，正比例函数与反比例函数的图象交于点，直线AB垂直于x轴，垂足为点C（点C在原点的右侧），并分别与正比例函数和反比例函数的图象相交于点A、B，且．

(1)求正比例函数和反比例函数的解析式：

(2)求的面积．

3．如图，直线与y轴交于A点，与反比例函数的图像交于点M，过M作轴于点H，且．

(1)请直接写出k的值；

(2)设点是反比例函数图像上的点，在y轴上是否存在点P，使得最小？若存在，求出点P的坐标；若不存在，请说明理由．

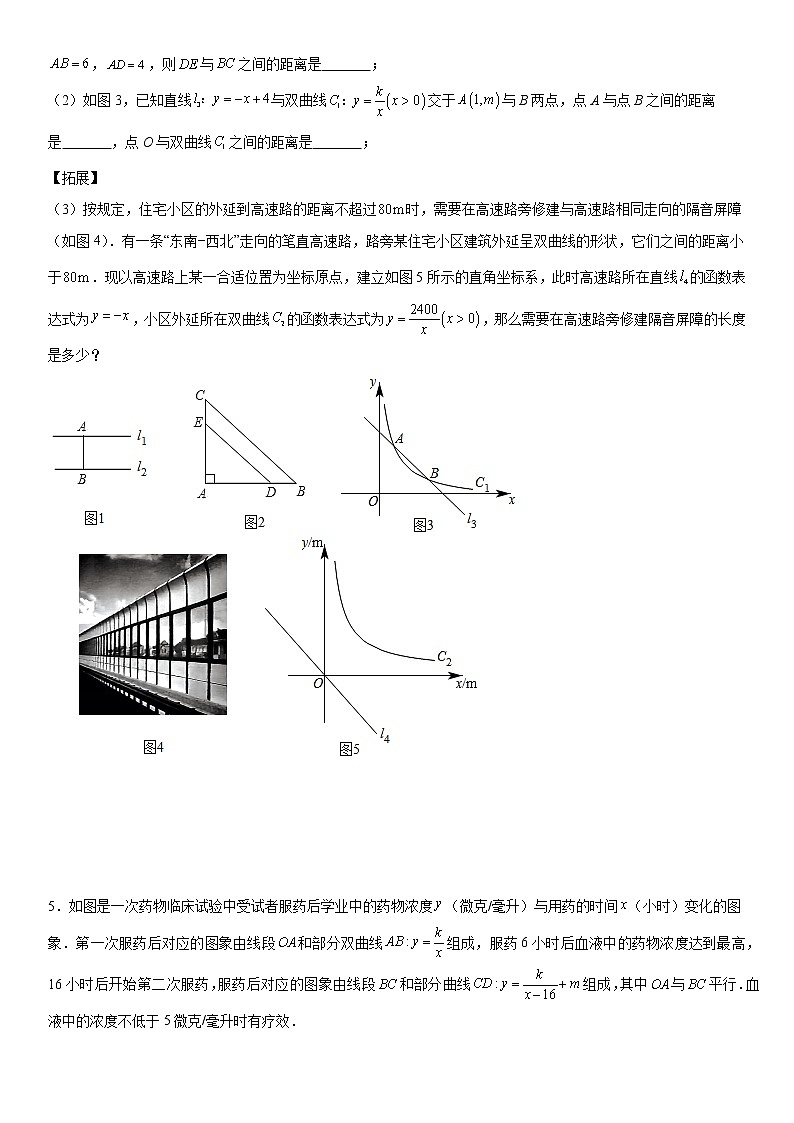
4．【定义】在平面内，把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值，称为这两个图形之间的距离，即A，B分别是图形M和图形N上任意一点，当的长最小时，称这个最小值为图形M与图形N之间的距离．

例如，如图1，，线段的长度称为点A与直线之间的距离，当时，线段的长度也是与之间的距离．

【应用】

（1）如图2，在等腰中，，，点D为边上一点，过点D作交于点E．若，，则与之间的距离是       ；

（2）如图3，已知直线与双曲线交于与B两点，点A与点B之间的距离是       ，点O与双曲线之间的距离是       ；

【拓展】

（3）按规定，住宅小区的外延到高速路的距离不超过时，需要在高速路旁修建与高速路相同走向的隔音屏障（如图4）．有一条“东南−西北”走向的笔直高速路，路旁某住宅小区建筑外延呈双曲线的形状，它们之间的距离小于．现以高速路上某一合适位置为坐标原点，建立如图5所示的直角坐标系，此时高速路所在直线的函数表达式为，小区外延所在双曲线的函数表达式为，那么需要在高速路旁修建隔音屏障的长度是多少？

5．如图是一次药物临床试验中受试者服药后学业中的药物浓度（微克/毫升）与用药的时间（小时）变化的图象．第一次服药后对应的图象由线段和部分双曲线组成，服药6小时后血液中的药物浓度达到最高，16小时后开始第二次服药，服药后对应的图象由线段和部分曲线组成，其中与平行．血液中的浓度不低于5微克/毫升时有疗效．

(1)分别求受试者第16小时，第22小时血液中的药物浓度；

(2)受试者第一次服药后第二次服药前这16小时内，有疗效的持续时间达到6小时吗?

(3)若血液中的药物浓度不高于4微克/毫升时才能进行第三次服药，问受试者第二次服药后至少经过几小时可进行第三次服药?

6．函数图象是研究函数的重要工具探究函数性质时，我们经历了列表、描点、连线画出函数图象，然后观察分析图象特征，概括函数性质的过程请结合已有的学习经验，画出函数的图象，并探究其性质．

(1)列表，并在平面直角坐标系中画出该函数的图象；

(2)观察函数图象，判断下列关于该函数性质的命题：

①当时，函数图象关于直线对称；

②当时，函数有最小值最小值为－2；

③时，函数y的值随x的增大而减小

其中正确的是______（请写出所有正确命题的序号）

(3)结合图象，请直接写出不等式的解集

7．如图，一次函数y＝kx＋n的图像经过点和点，与x轴交于点C，反比例函数经过点A和点B，．

(1)求反比例函数和直线AB的解析式；

(2)点为y轴上一动点，且∠AQB为钝角，求点Q的纵坐标t的取值范围；

(3)点D在直线AB上且在第二象限反比例函数图像的上方运动，过点D作x轴、y轴的垂线分别交反比例函数的图像于点F、E，直线EF分别交x轴、y轴于点N、M，设点D的横坐标为s，求的值．

8．有这样一个问题：探究函数的图象与性质，小童根据学习函数的经验，对函数的图象与性质进行研究，已知当时，；当时，．下面是小童探究的过程，请补充完整：

(1)该函数的解析式为______，______，______．

根据图中描出的点，画出函数图象．

(2)根据函数图象，下列关于函数性质的描述正确的是______；

①该函数图象是中心对称图形，它的对称中心是原点．

②该函数既无最大值也无最小值．

③在自变量的取值范围内，随的增大而减小．

(3)请结合（1）中函数图象，直接写出关于的不等式的解集．（保留1位小数）

9．小丽家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热，此过程中水温y（℃）与开机时间x（分）满足一次函数关系，当加热到100℃时自动停止加热，随后水温开始下降，此过程中水温y（℃）与开机时间x（分）成反比例关系，当水温降至20℃时，饮水机又自动开始加热……，重复上述程序（如图所示），根据图中提供的信息，解答问题：

(1)当时，求水温y（℃）与开机时间x（分）的函数关系式；

(2)求图中t的值；

(3)若小丽在通电开机后即外出散步，请你预测小丽散步70分钟回到家时，饮水机内的温度约为多少℃？

10．某项目化成果展示了一款简易电子秤：一个装有踏板（踏板质量忽略不计）的可变电阻，与踏板上人的质量m之间的函数关系式为，其图象如图1所示；图2的电路中，电源电压恒为12伏，定值电阻的阻值为40欧，接通开关，人站上踏板，电流表显示的读数为I安，该读数可以换算为人的质量m，电流表量程为0~0.2安．

温馨提示：①导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式；

②串联电路中电流处处相等，各电阻两端的电压之和等于总电压．

③测量过程电流不能超过电流表量程的最大值．

(1)用含I的代数式表示m．

(2)请确定该电子体重秤可称的最大质量．

(3)为了将电子体重秤可称的最大质量调高至115千克，在不更换原来电流表及量程条件下，小明用方案一、二、三来进行解决问题．请填写下表：

11．如图， A是双曲线上一点，连接OA，将线段OA绕点O顺时针旋转得到线段OB，点恰在直线上，这条直线与双曲线公共点的横坐标是6．

(1)画出题中的直线，求反比例函数的解析式．

(2)求点的坐标．

12．近两年，人们与新冠病毒进行着长期的抗争．每周末，学校都要对教室采进行消杀．已知消杀时，教室内每立方米空气中的含药量（毫克）与时间（分钟）成正比例；消杀后，与成反比例（如图所示）．现测得消杀8分钟结束时，教室内空气中每立方米的含药量为6毫克，请你根据题中所提供的信息，解答下列问题．

(1)消杀时关于的函数关系式为________，自变量的取值范围是________；消杀后与的函数关系式为________；

(2)研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消杀是否有效？为什么?

13．如图，正比例函数与反比例函数的图象交于点A，经过点A作轴于点B，，点C在线段AB上，．

(1)求反比例函数的表达式；

(2)点P在y轴上，当与的面积相等时，求点P的坐标．

14．如图，一次函数的图像交x轴于点，交y轴于点，与反比例函数的图像交于A、B两点，点A的横坐标为6

(1)求一次函数与反比例函数的解析式，并在平面直角坐标系中画出反比例函数的图像；

(2)请写出反比例函数图象的一条性质：______．

(3)在y轴上是否存在一点M，使得的面积是面积的2倍？若存在，请求出点M的坐标；若不存在，请说明理由

15．如图，一次函数经过点，，与反比例函数的图象交于点，D两点．

(1)求反比例函数和一次函数的解析式；

(2)结合函数图象，直接写出当时x的取值范围；

(3)点P在x轴上，是否存在是以CD为腰的等腰三角形，若存在，请直接写出点P的坐标；若不存在，说明理由．

16．疫情防控期间，某校校医每天早上对全校办公室和教室进行药物喷洒消毒，完成1间办公室和1间教室的喷洒共需；完成2间办公室和3教室的喷洒共需．

(1)该校医完成一间办公室和一间教室的药物喷洒各需多少时间？

(2)消毒药物在一间教室内空气中的浓度（单位：与时间（单位：的函数关系如图所示，校医进行药物喷洒时与的函数关系式为，药物喷洒完成后与成反比例函数关系，两个函数图象的交点为点．当教室空气中的药物浓度不高于时，对人体健康无危害，校医依次对（1）班至班教室（共11间）进行药物喷洒消毒，当把最后一间教室药物喷洒完成后，（1）班学生能否进入教室？请通过计算说明．

17．反比例函数的图象如图所示，一次函数（）的图象与的图象交于，两点，

(1)求一次函数的表达式，并在所给的平面直角坐标系中面出该函数的图象；

(2)观察图象，直接写出不等式的解集；

(3)一次函数的图象与x轴交于点C，连接，求的面积．

参考答案：

1．(1)y1=x-1，y2=；

(2)-2＜x＜0或x＞4；

(3)点C的坐标为（，0）或（-，0）．

2．(1)；

(2)3或

3．(1)6

(2)存在，

4．（1）；（2），；（3）80米

5．(1)第16小时的血液浓度为3微克/毫升，第22小时的血液浓度为11微克/毫升

(2)不超过6小时

(3)48小时

6．(1)11

(2)②③

(3)x＜﹣2或0＜x＜2

7．(1)，

(2)，且

(3)

8．(1)，，

(2)②

(3)或

9．(1)

(2)

(3)

10．(1)

(2)110

11．(1)双曲线解析式为

(2)点的坐标为，或

12．(1)，；

(2)有效

13．(1)

(2)点P的坐标为或

14．(1)，，

(2)答案不唯一

(3)存在，或

15．(1)；

(2)或

(3)存在，点的坐标为或

16．(1)校医完成一间办公室和一间教室的药物喷洒各要和

(2)一班学生能安全进入教室

17．(1)一次函数的表达式为

(2)或

(3)2