2023年广东省深圳市龙华区中考一模数学试卷

这是一份2023年广东省深圳市龙华区中考一模数学试卷，文件包含2023年广东省深圳市龙华区中考一模数学试卷解析版docx、2023年广东省深圳市龙华区中考一模数学试卷原卷版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
1. 将两本相同的书进行叠放，得到如图所示的几何体，则它的主视图是（ ）
A. B.
C. D.
2. 国家卫健委网站消息：截至2022年5月27日，31个省（自治区，直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗超过33亿剂次，用科学记数法表示33亿是（ ）
A. B. C. D.
3. 某人从一袋黄豆中取出粒染成蓝色后放回袋中并混合均匀，接着抓出粒黄豆，数出其中有粒蓝色的黄豆，则估计这袋黄豆约有（ ）
A. 粒B. 粒C. 粒D. 粒
4. 下列各运算中，计算正确的是（ ）
A a+a＝a2B. （3a2）3＝9a6
C. （a+b）2＝a2+b2D. 2a•3a＝6a2
5. 某学习小组5名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、89分，则下列结论正确的是（ ）
A. 平均分是91B. 众数是94C. 中位数是90D. 极差是8
6. 已知反比例函数，当＜0时，随的增大而增大，则的值可能是（ ）
A. 3B. 2C. 1D. -1
7. 下列说法正确的是（ ）
A. 若点C是线段AB的黄金分割点，AB=2，则AC=
B. 平面内，经过矩形对角线交点的直线，一定能平分它的面积
C. 两个正六边形一定位似
D. 菱形两条对角线互相垂直且相等
8. 数学兴趣小组的同学们来到宝安区海淀广场，设计用手电来测量广场附近某大厦的高度，如图，点处放一水平的平面镜．光线从点出发经平面镜反射后刚好射到大厦的顶端处，已知，，且测得米，米，米，那么该大厦的高度约为（ ）
A 米B. 米C. 米D. 米
9. 如图，直线∥∥，△ABC的边AB被这组平行线截成四等份，△ABC的面积为32，则图中阴影部分四边形DFIG的面积是（ ）
A. 12B. 16C. 20D. 24
10. 如图，正方形ABCD中，AB=4，点E是BA延长线上一点，点M、N分别为边AB、BC上的点，且AM=BN=1，连接CM、ND，过点M作MF∥ND与∠EAD的平分线交于点F，连接CF分别与AD、ND交于点G、H，连接MH，则下列结论正确的有（ ）个
①MC⊥ND；②sin∠MFC=；③(BM+DG)²=AM²+AG²；④S△HMF=
A. 1B. 2C. 3D. 4
二、填空题（本大题共5小题，每小题3分，共15分）
11. 已知，则代数式_____________.
12. 如图，是一条笔直的公路，道路管理部门在点A设置了一个速度监测点，已知BC为公路的一段，B在点A的北偏西30°方向，C在点A的东北方向，若AB=50米.则BC的长为__________米.（结果保留根号）
13. 在一个不透明的口袋中，装有若干个红球和7个黄球，它们只有颜色不同，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率稳定在0.7，则估计口袋中大约有红球 _____个．
14. 若直角三角形斜边上的高是3，斜边上的中线是6，则这个直角三角形的面积是 _____．
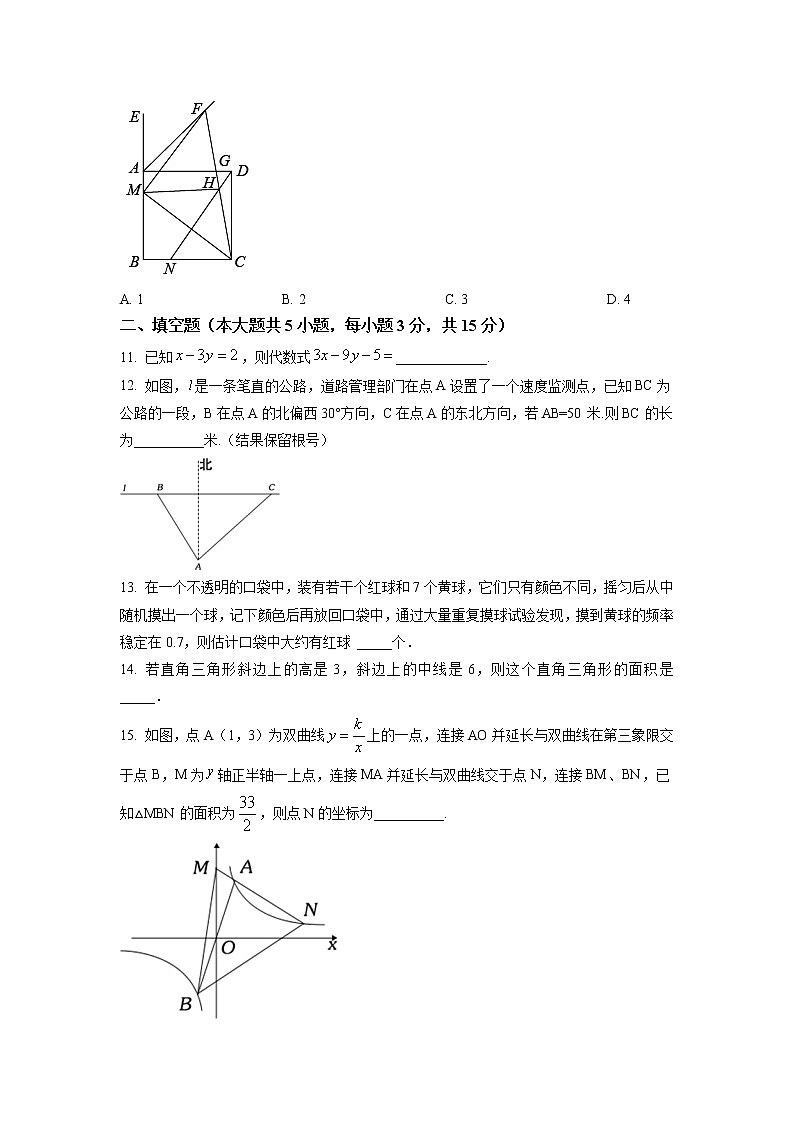
15. 如图，点A（1，3）为双曲线上的一点，连接AO并延长与双曲线在第三象限交于点B，M为轴正半轴一上点，连接MA并延长与双曲线交于点N，连接BM、BN，已知△MBN的面积为，则点N的坐标为__________.
三、解答题（本题共7小题，其中第16题5分，第17题6分，第18题8分，第19题8分，第20题8分，第21题10分，第22题10分.共55分）
16. 计算：.
17. 先化简，再求值：，其中．
18. 习近平指出：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．”为了解学生的阅读情况，佳佳从七、八年级分别随机抽查了40名学生（已知两个年级学生人数相同），调查了他们在校期间的阅读情况，根据调查情况得到如下统计图表：
（1）a＝_____；
（2）八年级参加阅读学生的平均阅读时间的中位数为______；
（3）七年级学生参加阅读人数的众数为______；
（4）估计该校七、八年级共1120名学生中这五天平均每天参加阅读的人数．
19. 如图，已知射线BC⊥AB，以AB为斜边作Rt△ABD，延长AD到E，使得AD＝DE，连接BE，BF平分∠CBE交AE于点F．
（1）求证：BD＝DF；
（2）若AB＝2，以AE为边向下作∠AEG＝45°，交射线BC于点G，求BG的长．
20. 某新型高科技商品，每件的售价比进价多6元，5件的进价相当于4件的售价，每天可售出200件，经市场调查发现，如果每件商品涨价1元，每天就会少卖5件．
（1）该商品的售价和进价分别是多少元？
（2）设每天的销售利润为元，每件商品涨价元，则当售价为多少元时，该商品每天的销售利润最大，最大利润为多少元？
21. 【探究函数的图象与性质】
（1）函数的自变量x的取值范围是 ；
（2）下列四个函数图象中，函数的图象大致是 ；
（3）对于函数，求当时，y的取值范围．请将下列的求解过程补充完整．
解：∵，∴______．
∵，∴____．
【拓展说明】
（4）若函数，求y的取值范围．
22. 如图1，已知点G在正方形的对角线上，，垂足为点E，，垂足为点F．
（1）证明与推断：
②求证：四边形是正方形；
②推断：的值为___________；
（2）探究与证明：
将正方形的绕点C顺时针方向旋转，如图2所示，试探究线段与之间的数量关系，并说明理由；
（3）拓展与运用：
正方形旋转过程中，当B、E、F三点在一条直线上时，如图3所示，延长交于点H，若，则___________．年级
参加阅读人数
星期一
星期二
星期三
星期四
星期五
七年级
25
30
a
40
30
八年级
20
26
24
30
40
合计
45
56
59
70
70