冀教版八年级上册第十二章 分式和分式方程12.4 分式方程教学ppt课件

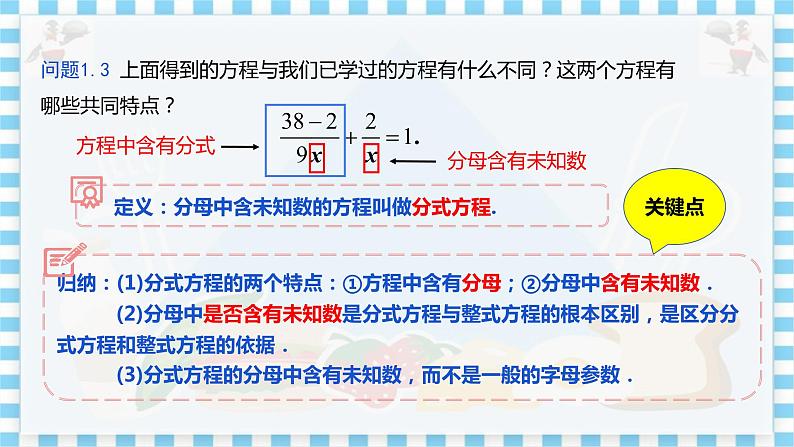
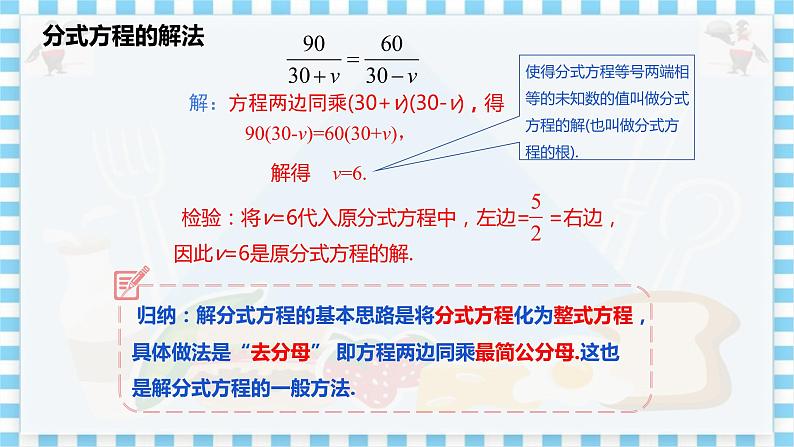
教学目标

1.经历从实际问题中建立分式方程的过程.

2.了解分式方程、分式方程的解、分式方程的增根.

3.会解分式方程，会检验根的合理性.

教学重难点

重点：理解分式方程、分式方程的解、分式方程的增根的概念；

难点：会解分式方程，会检验根的合理性.

教学过程

旧知回顾

1.回忆整式方程的定义；

    2.回忆整式方程的解法.

导入新课

1.分式方程的定义

小红家到学校的路程为38 km.小红从家去学校总是先乘公共汽车，下车后再步行2 km，才能到学校，路途所用时间是1 h.已知公共汽车的速度是小红步行速度的9倍，求小红步行的速度.

问题1：上述问题中有哪些等量关系？

问题2：根据你所发现的等量关系，设未知数并列出方程.

（教师组织学生讨论，提问学生，师生互动）

学生讨论会发现：

问题中的等量关系为：

(1)小红乘公共汽车的时间+小红步行的时间＝小红上学路上的时间；

(2)公共汽车的速度＝9×小红步行的速度.

如果设小红步行的速度为x km/h，那么公共汽车的速度为9x km/h，

根据等量关系(1)，可得到方程

如果设小红步行的时间为x h，那么她乘公共汽车的时间为(1－x) h，

根据等量关系(2)，可得到方程

问题3：上面得到的方程与我们已学过的方程有什么不同？这两个方程有哪些共同特点？

这些方程的分母中含有未知数.

结论：分式方程的定义

分母中含有未知数的方程叫做分式方程.

归纳：(1)分式方程的两个特点：①方程中含有分母；②分母中含有未知数．

      (2)分母中是否含有未知数是分式方程与整式方程的根本区别，是区分

分式方程和整式方程的依据．

(3)分式方程的分母中含有未知数，而不是一般的字母参数．

练一练：1.判断下列方程是不是分式方程？

；  ；  ；

；    .

2.下列各项属于分式方程的是(       )

A.   B.   C.   D.

（教师引导，学生分析）

学生通过听课已经对分式方程有了一定的认识，让学生独立思考，通过回答规范他们对分式方程的认识.

解：1.√ √ × × ×    2.D

2.分式方程的解法

问题：我们学习过整式方程的解法，试着解下面这个分式方程.

.

（教师引导，学生分析）

①转化为整式方程——去分母          1化

根据等式的性质，等式两边同时乘最简公分母——(30+v)(30-v)

②得到整式方程，解方程——90（30-v）＝60（30+v），v＝6        2解

③检验所得结果是否正确——将结果代入分式方程后，等号两边是否相等

完成解答过程：                                           3检验

.

解：方程两边同乘(30+v)(30-v)，得

90(30-v)＝60(30+v)，

解得   v＝6.

检验：将v＝6代入原分式方程中，左边＝ ＝右边，

 因此v＝6是原分式方程的解.

在这里使得分式方程等号两端相等的未知数的值叫做分式方程的解(也叫做分式方程的根).

归纳：解分式方程的基本思路是将分式方程化为整式方程，具体做法是“去分母” 即方程两边同乘最简公分母.这也是解分式方程的一般方法.

例1　解方程:

按照解分式方程的步骤进行.

解：(1) 方程两边同乘x(1-x),得36x＝18(1－x).

解这个整式方程，得 x＝.

经检验，x＝ 是原分式方程的解.

(2)    方程两边同乘9x,得36＋18＝9x，

解这个整式方程，得x＝6.

经检验，x＝6 是原分式方程的解.

归纳：(1)解分式方程的基本思想是“化整”，即“化分式方程为整式方程”，   而“化整”的关键是找最简公分母.

(2)解分式方程一定要注意验根，验根是解分式方程必不可少的步骤．

(3)在去分母时，方程两边同乘最简公分母，必须每一项都要乘，不能认为有分母的就要乘，没有分母的就不用乘，而是有几项就要乘几项，不能漏乘．

练一练：

1.解分式方程 时，去分母后变形为(       )

A. 2+(x+2)＝3        B. 2-(x+2)＝3(1-x)

C. 2-x+2＝3(x-1)       D. 2-(x+2)＝3(x-1)

2.分式方程  的解是(       )

A. x＝1   B. x＝-1      C. x＝3     D. x＝-3

答案：（1）D　（2）A

3.分式方程的增根

问题：下面是小华解分式方程 的过程：

      方程两边同乘x－1，得x＋1＝－(x－3)＋(x－1).

      解这个整式方程，得x＝1.

      你认为x＝1是方程 的解吗？为什么?

（教师引导，学生分析）

事实上，因为当x＝1时，x－1＝0，即这个分式方程的分母为0，方程中的分式无意义，所以x＝1不是这个分式方程的解(根).

归纳：分式方程根的检验：

在解分式方程时，首先是通过去分母将分式方程转化为整式方程，并解这个整式方程，然后要将整式方程的根代入分式方程（或公分母）中检验.当分母的值不等于0 时，这个整式方程的根就是分式方程的根；当分母的值为0 时，分式方程无解，我们把这样的根叫做分式方程的增根.

总结：分式方程增根的条件：

①是整式方程的根；

②使分式方程的分母（或公分母）为0 .

例2  解方程：.

解：方程两边同乘x+2，得2- (2-x)＝3(x+2)，

 解这个整式方程，得  x＝-3，

 经检验，x＝-3是原分式方程的解.

例3   若关于x的方程有增根，求m 的值 .

分析：增根的条件是①使分式方程的分母等于0，②是整式方程的根，即x-3＝0,x＝3;同时x＝3是整式方程的根，应将x＝3代入整式方程.

解：方程两边同乘x-3,得

  2-(x-3)＝m，解得，x＝5-m.

∵ 分式方程有增根，∴ x-3＝0.

∴ x＝3，把x＝3代入 x＝5-m,得 3＝5-m，∴ m＝2.

课堂练习

1.有下列关于x，y的方程：

①；②；③（a,b为常数）；④ .其中分式方程有(   )

 A.1个          B.2个        C.3个         D.4个

2.分式方程 的解为(   )

A. x＝1          B. x＝-1      C.无解        D. x＝-2

3.关于x的方程 有增根，则m的值是(   )

A. -5             B.5            C.-7           D.2

4.若关于x的方程的解为正数，则m的取值范围是(    )

A.m＜6      B.m＞6     C.m＜6且m≠0     D.m＞6且m≠8

5.解方程：；   .      

参考答案

1.B  2.C  3.A  4.C

5.解：(1)方程两边同乘x-3，得 x＝2(x-3)+3，

解这个整式方程，得x＝3，

检验：当x＝3时，x-3＝0.

所以x＝3是原分式方程的增根.

所以原分式方程无解.

(2)方程两边同乘（x-2)(x+2),得 4（x+2)＝16-3(x-2)，

    解这个整式方程，得x＝2.

检验：当x＝2时，（x+2)(x-2)＝0，

    所以x＝2是原分式方程的增根.

所以原分式方程无解.

课堂小结

1.分式方程的定义：

分母中含有未知数的方程叫做分式方程

2.解分式方程：

解分式方程的一般步骤：一化   二解    三检验

3.分式方程的增根：

（1）分式方程有增根时的应用：①最简公分母为0，求增根；②将增根代入整式方程求其他参数.

（2）分式方程无解：①分式方程有增根；②化为的整式方程无解.

布置作业

完成教材第20页习题A组，B组.

板书设计

12.4　分式方程

教学反思

教学反思

教学反思

教学反思

教学反思