第23练 空间点、直线、平面之间的位置关系-高考数学一轮复习小题多维练（新高考专用）

专题07  立体几何初步

第23练 空间点、直线、平面之间的位置关系

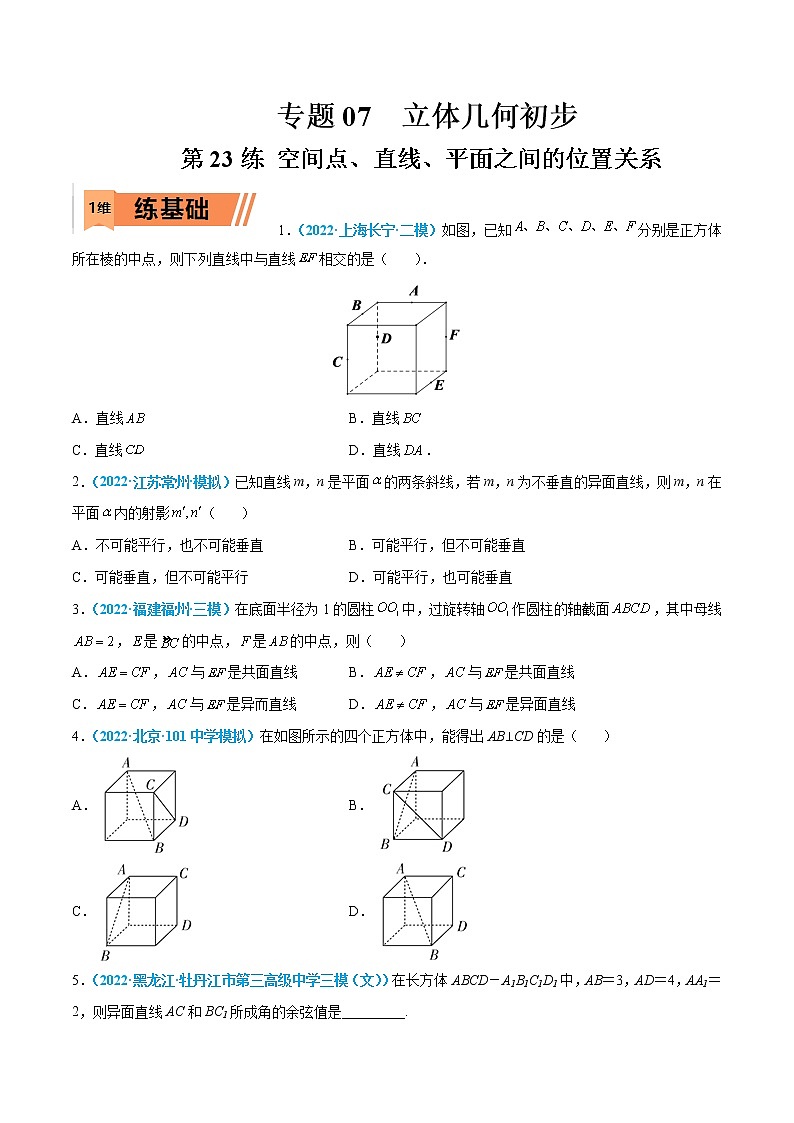
1．（2022·上海长宁·二模）如图，已知分别是正方体所在棱的中点，则下列直线中与直线相交的是（       ）．

A．直线  B．直线

C．直线  D．直线．

【答案】A

【解析】如图，易知，所以，且，

所以为梯形，故与EF相交，A正确；

因为，所以，故B错误；

因为平面CDH平面EFNL，平面CDH，平面EFNL，

所以直线CD与直线EF无公共点，故C错误；

因为平面ADF，平面，故AD与EF异面，D错误.

故选：A

2．（2022·江苏常州·模拟）已知直线m，n是平面的两条斜线，若m，n为不垂直的异面直线，则m，n在平面内的射影（       ）

A．不可能平行，也不可能垂直 B．可能平行，但不可能垂直

C．可能垂直，但不可能平行 D．可能平行，也可能垂直

【答案】D

【解析】如图，在正方体中，即为，为，底面为平面，则m，n在平面内的射影和垂直；

如图，在正方体中，即为，为，底面为平面，则m，n在平面内的射影和平行；

综上，m，n在平面内的射影可能平行，也可能垂直.

故选：D.

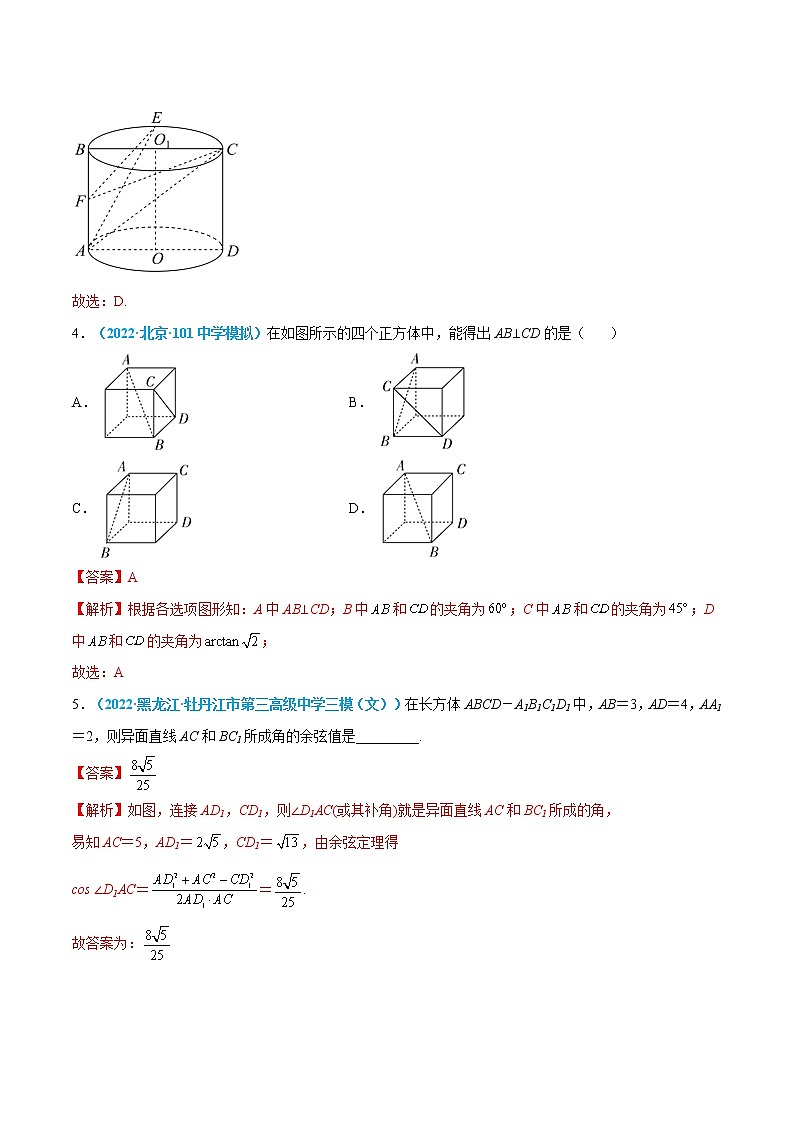
3．（2022·福建福州·三模）在底面半径为1的圆柱中，过旋转轴作圆柱的轴截面，其中母线，是的中点，是的中点，则（       ）

A．，与是共面直线 B．，与是共面直线

C．，与是异而直线 D．，与是异面直线

【答案】D

【解析】解：由题意，圆柱的轴截面为边长为2的正方形，

是的中点，是的中点，

所以平面ABC,与平面ABC相交，且与AC无交点，

所以与是异面直线；

又，所以.

故选：D.

4．（2022·北京·101中学模拟）在如图所示的四个正方体中，能得出AB⊥CD的是（       ）

A． B．

C． D．

【答案】A

【解析】根据各选项图形知：A中AB⊥CD；B中和的夹角为；C中和的夹角为；D中和的夹角为；

故选：A

5．（2022·黑龙江·牡丹江市第三高级中学三模（文））在长方体ABCD－A1B1C1D1中，AB＝3，AD＝4，AA1＝2，则异面直线AC和BC1所成角的余弦值是_________.

【答案】

【解析】如图，连接AD1，CD1，则∠D1AC(或其补角)就是异面直线AC和BC1所成的角，

易知AC＝5，AD1＝，CD1＝，由余弦定理得

cos ∠D1AC＝＝.

故答案为：

6．（2022·山东济南·二模）下列命题：

①平行于同一条直线的两条直线平行；

②如果平面外的一条直线平行于平面内的一条直线，那么该直线与这个平面平行；

③如果一个平面内的两条相交直线分别平行于另一个平面，那么这两个平面平行；

④如果一条直线和平面内的两条直线垂直，那么该直线垂直于这个平面；

⑤如果一条直线和平面的一条斜线在平面内的射影垂直，那么直线也和斜线垂直．

其中正确命题的序号为______．

【答案】①②③

【解析】①，根据平行公理可知：平行于同一条直线的两条直线平行.所以①正确，

②，根据线面平行的判定定理可知：如果平面外的一条直线平行于平面内的一条直线，那么该直线与这个平面平行，所以②正确.

③，结合面面平行的判定定理可知：如果一个平面内的两条相交直线分别平行于另一个平面，那么这两个平面平行.所以③正确.

④，如果一条直线和平面内的两条直线垂直，那么该直线可能在这个平面内，所以④错误.

⑤，如果一条直线和平面的一条斜线在平面内的射影垂直，直线时，，但与不垂直.所以⑤错误.

故答案为：①②③

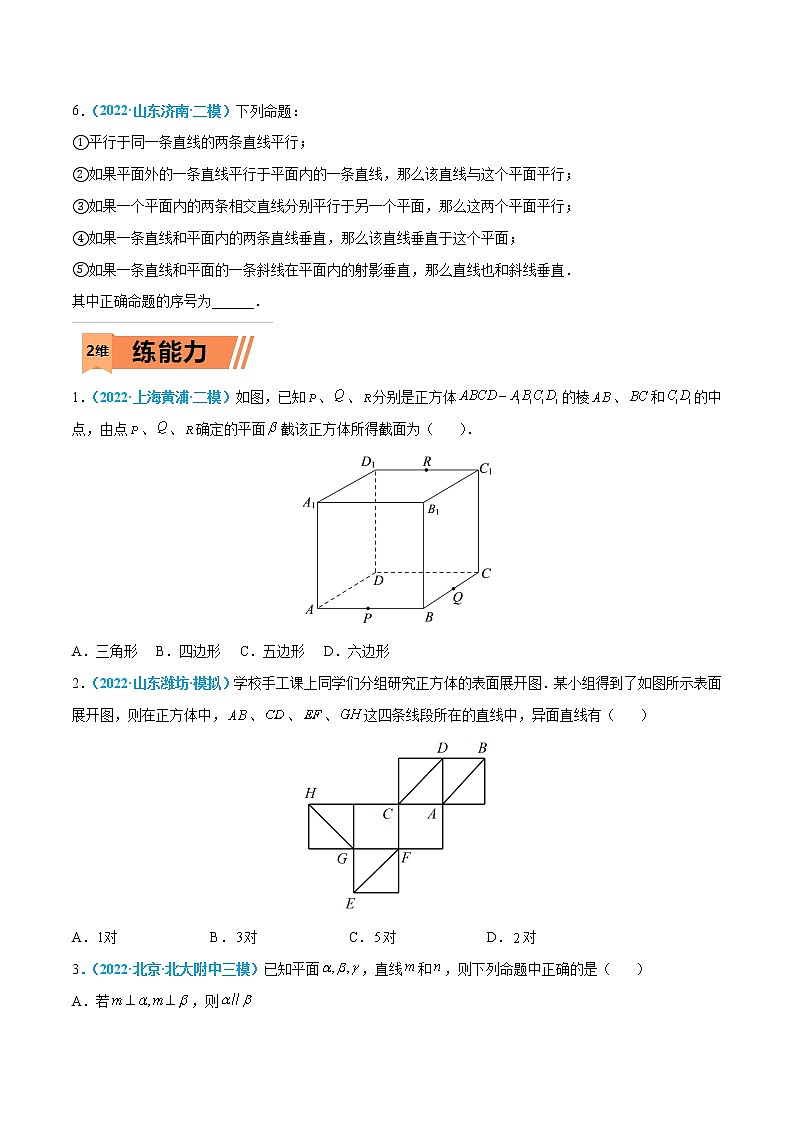
1．（2022·上海黄浦·二模）如图，已知、、分别是正方体的棱、和的中点，由点、、确定的平面截该正方体所得截面为（       ）．

A．三角形 B．四边形 C．五边形 D．六边形

【答案】D

【解析】如图，分别取的中点、、，连接，

由正方体性质，所以平面，且，又交于同一点，所以平面，所以点、、确定的平面即为六边形

故选：D．

2．（2022·山东潍坊·模拟）学校手工课上同学们分组研究正方体的表面展开图．某小组得到了如图所示表面展开图，则在正方体中，、、、这四条线段所在的直线中，异面直线有（       ）

A．对 B．对 C．对 D．对

【答案】B

【解析】作出正方体的图形如下图所示：

则与、与、与是异面直线，共对.

故选：B.

3．（2022·北京·北大附中三模）已知平面，直线和，则下列命题中正确的是（       ）

A．若，则

B．若，则

C．若，则

D．若，则

【答案】A

【解析】选项A正确，因为垂直于同一直线的两个平面互相平行；

选项B错误，平面和也可以相交；

选项C错误，直线可能在平面内；

选项D错误，直线和还可能相交或者异面.

故选：A.

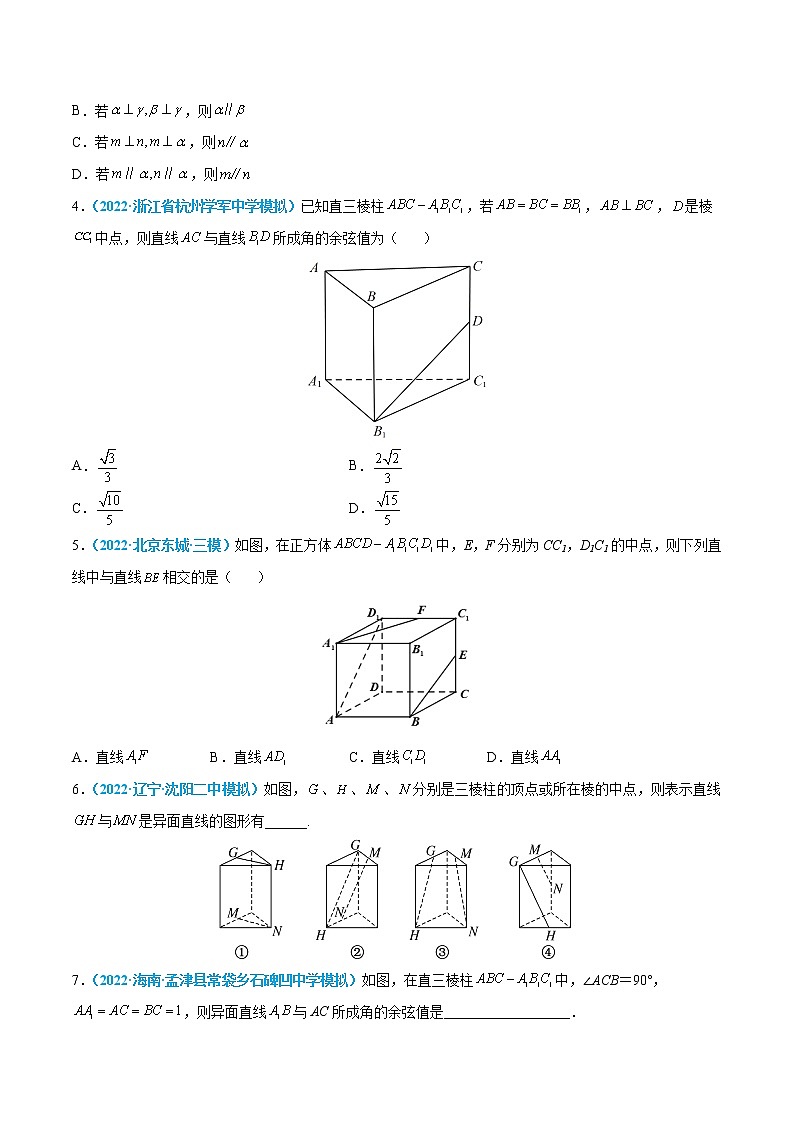
4．（2022·浙江省杭州学军中学模拟）已知直三棱柱，若，，是棱中点，则直线与直线所成角的余弦值为（       ）

A． B．

C． D．

【答案】C

【解析】若为中点，连接，又是棱中点，

所以，在直三棱柱中且，即为平行四边形，

所以，则直线与直线所成角即为，

若，则，，

所以.

故选：C

5．（2022·北京东城·三模）如图，在正方体中，E，F分别为CC1，D1C1的中点，则下列直线中与直线相交的是（       ）

A．直线  B．直线  C．直线  D．直线

【答案】A

【解析】连接，则，

由，可得四边形为平行四边形，

∴，，

所以，即四边形为梯形，

故直线与直线相交，

直线与直线为异面直线，直线与直线为异面直线，直线与直线为异面直线.

故选：A.

6．（2022·辽宁·沈阳二中模拟）如图，、、、分别是三棱柱的顶点或所在棱的中点，则表示直线与是异面直线的图形有______.

【答案】②④

【解析】解：根据题意，

在①中，且，则四边形是平行四边形，有，不是异面直线；

图②中，、、三点共面，但面，因此直线与异面；

在③中，、分别是所在棱的中点，所以且，故，必相交，不是异面直线；

图④中，、、共面，但面，与异面．

所以图②④中与异面．

故答案为：②④.

7．（2022·海南·孟津县常袋乡石碑凹中学模拟）如图，在直三棱柱中，∠ACB＝90°，，则异面直线与AC所成角的余弦值是__________________．

【答案】

【解析】解：连结，∵AC∥，

∴是异面直线与AC所成角（或所成角的补角），

∵在直三棱柱中，∠ACB＝90°，，

∴，，，，

∴

∴异面直线与AC所成角的余弦值为．

故答案为：．

8．（2022·四川·绵阳中学实验学校模拟（文））已知正三棱柱的所有棱长均相等，直线与所成的角为，则______

【答案】

【解析】设分别为中点，连接，

，，

直线与所成角为的补角，即；

设正三棱柱的棱长为，

，，，，

，

，

则，

又，

.

故答案为：.

1．（2022·山东聊城·二模）已知某圆锥的侧面积等于底面的3倍，直线是底面所在平面内的一条直线，则该直线与母线所成的角的余弦值的取值范围为（       ）

A． B．

C． D．

【答案】A

【解析】设底面圆的半径为，母线长为，因为圆锥的侧面积等于底面的3倍，

所以，即，因为直线与直线所成角的范围为，

所以当直线与底面圆相切时，直线与母线所成角最大为，则该直线与母线所成的角的余弦值的最小值为；

当直线过底面圆的圆心时，由线面角的定义可知，此时直线与母线所成角最小，则该直线与母线所成的角的余弦值的最大值为，

即该直线与母线所成的角的余弦值的取值范围为.

故选：A

2．（2022·浙江省义乌中学模拟）直线平面，直线平面，则“”是“”的（       ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】B

【解析】因为直线平面，直线平面，若，则、平行、相交或重合，

即“”“”；

若，则直线平面，设过直线的平面与平面相交，交线为，

因为直线平面，直线平面，平面平面直线，所以，直线直线，

因为直线平面，直线平面，所以，直线直线，故直线直线，

即“”“”.

因此，“”是“”的必要不充分条件.

故选：B.

3．（2022·福建莆田·模拟）莆田妈祖城有一钟楼，其顶部可视为正四棱柱与正四棱锥的组合体，如图，四个大钟分布在正四棱柱的四个侧面，则每天0点至12点（包含0点，不含12点）相邻两钟面上的时针成60°角的次数是（       ）

A．2 B．4 C．6 D．8

【答案】B

【解析】由题设，在0、6点时相邻钟面上的时针都平行，即夹角为0度；在3、9点时相邻钟面上的时针垂直，即夹角为90度，

所以相邻钟面上的时针，在、、、点之间各有一次成60°角的情况，故共有4次成60°角.故选：B

4．（2022·重庆南开中学模拟）如图，在三棱锥中，，，，分别是，的中点．则异面直线，所成角的余弦值为（       ）

A． B． C． D．

【答案】C

【解析】解：如图，连接，取的中点，连接，

因为是中点，则，

所以（或其补角）就是异面直线所成的角，

由已知，，，

所以，

所以异面直线，所成角的余弦值为

故选：C．

5．（2022·广东·模拟）已知是空间中两条互相垂直的异面直线，则下列说法正确的是（       ）

A．存在平面，使得且

B．存在平面，使得且

C．存在平面，使得

D．存在平面，使得

【答案】ABD

【解析】如下图，可知A、B、D都正确，而满足C的平面不存在.

故选：ABD.

6．（2022·广东·模拟）如图，在正三棱柱中，，，则下列结论正确的是（       ）

A．不存在，使得异面直线与垂直

B．当时，异面直线和所成角的余弦值为

C．若，当时，三棱锥的外接球的表面积为

D．过且与直线和直线所成角都是的直线有两条

【答案】ABC

【解析】对于A，假设存在满足题意，使得，又，，所以平面，所以，这与是正三角形矛盾，所以假设不成立，故A正确；

对于B，当时，，如图1，

取靠近点的三等分点，连接，，易得，所以四边形是平行四边形，则，所以或其补角即为异面直线和所成的角，设，则，，在中，由余弦定理得，故B正确；

对于C，，当时，结合正弦定理可得得外接圆的半径，设外接圆的圆心为，三棱锥的外接球球心为，半径为，如图2，

易知，，所以三棱锥的外接球的表面积为，故C正确；

对于D，在平面和平面内，过点分别作直线和直线的平行线和，由异而直线所成的角的定义知：过的直线与直线和直线所成角与过的直线与直线和所成角相等，如图3，过作；

如图4，过作，使得；

如图5，过作，使得，共三条，故D错误.

故选：ABC．

7．（2022·山东威海·三模）已知是两个不同的平面，m、n是平面及外两条不同的直线，给出四个论断：①，②，③，④，则正确的是(       )

A．②③④① B．①③④② C．①②④③ D．①②③④

【答案】AC

【解析】对于A，若，，则m⊥β，又∵，∴m⊥n，故A正确；

对于B，若，，则n∥α，有∵，∴α与β平行或相交，故B错误；

对于C，若，，则m⊥β，又∵，nβ，∴n∥β，故C正确；

对于D，若，，则n∥α，又∵，则m与α平行或相交，故D错误．

故选：AC．

8．（2022·湖北·模拟）已知四面体中，，，，直线AB与CD所成角为，则下列说法正确的是（       ）

A．AD的取值可能为 B．AD与BC所成角余弦值一定为

C．四面体ABCD体积一定为 D．四面体ABCD的外接球的半径可能为

【答案】ACD

【解析】由题可知，，，则可将四面体ABCD的四个顶点放入如下图所示的直三棱柱中，考虑到直线AB与CD所成角为，故有如下两种情况：

对于左图，，则，；此时AD与BC所成角余弦值为；所以选项A正确；

因为，

所以；

分别取三棱柱上下底面三角形的外心G，H，连接GH，则线段GH的中点O即为三棱柱外接球球心，也即为四面体ABCD的外接球心，

故四面体ABCD的外接球半径．

对于右图，，则，；

此时AD与BC所成角余弦值为，所以选项B错误；

因为，

所以，所以选项C正确；

同上可得四面体ABCD的外接球半径．

所以选项D正确.

故选：ACD．

9．（2022·山东日照·二模）在棱长为3的正方体中，已知点P为棱上靠近点的三等分点，点Q为棱CD上一动点.若M为平面与平面ABCD的公共点，且点M在正方体的表面上，则所有满足条件的点M构成的区域面积为___________.

【答案】

【解析】延长DA，交于点N，连接NQ交AB于点E，

则线段EQ为平面与平面ABCD的公共点M的集合，

当Q运动到点D时，E与A重合；当Q运动到点C时，

设此时E点运动到F点，则梯形FADC即为点M构成的区域，

因为∽，所以，

所以，所以.

故答案为：.

10．（2022·福建莆田·三模）在正方体中，，，，分别是棱，，，的中点，则异面直线与所成角的余弦值是______．

【答案】

【解析】如图

连接，取中点为点,连接，，

且

四边形为平行四边形

同理

异面直线与所成角即为直线与所成角

设正方体的棱长为，则，，   

在中，

故答案为： .