




专题09 空间向量与立体几何-高考数学一轮复习小题多维练(新高考专用)
展开专题09 空间向量与立体几何
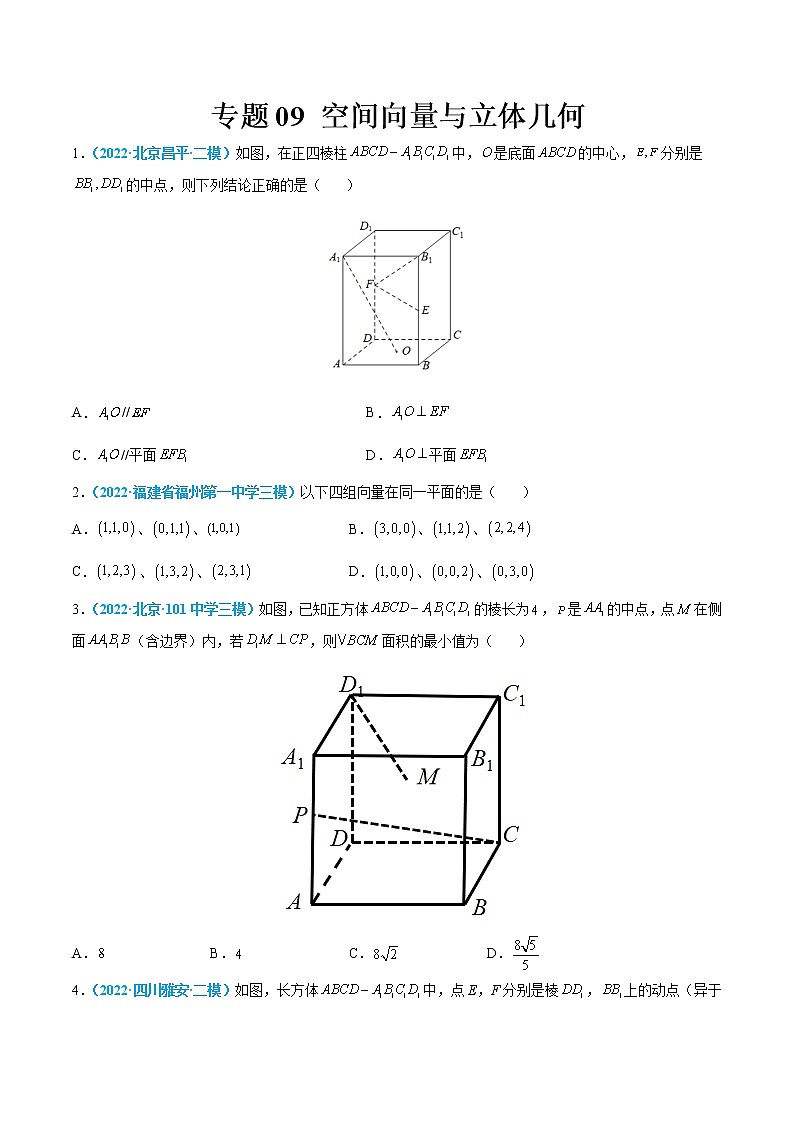
1.(2022·北京昌平·二模)如图,在正四棱柱中,是底面的中心,分别是的中点,则下列结论正确的是( )
A.// B.
C.//平面 D.平面
2.(2022·福建省福州第一中学三模)以下四组向量在同一平面的是( )
A.、、 B.、、
C.、、 D.、、
3.(2022·北京·101中学三模)如图,已知正方体的棱长为,是的中点,点在侧面(含边界)内,若,则面积的最小值为( )
A. B. C. D.
4.(2022·四川雅安·二模)如图,长方体中,点E,F分别是棱,上的动点(异于所在棱的端点).给出以下结论:①在F运动的过程中,直线能与AE平行;②直线与EF必然异面;③设直线AE,AF分别与平面相交于点P,Q,则点可能在直线PQ上.其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
5.(2022·山东泰安·二模)已知A,B两点都在以PC为直径的球O的球面上,AB⊥BC,AB=BC=4,若球O的体积为,则异面直线PB与AC所成角的余弦值为( )
A. B.
C. D.
6.(2022·浙江嘉兴·模拟)如图,在矩形中,,E,F,G,H分别为边的中点,将分别沿直线翻折形成四棱锥,下列说法正确的是( )
A.异面直线所成角的取值范围是
B.异面直线所成角的取值范围是
C.异面直线所成角的取值范围是
D.异面直线所成角的取值范围是
7.(2022·安徽·合肥市第八中学模拟(理))平行六面体中,,则与底面所成的线面角的正弦值是( )
A. B. C. D.
8.(2022·安徽合肥·二模(文))在直三棱柱中,,,为该三棱柱表面上一动点,若,则点的轨迹长度为( )
A. B.
C. D.
9.(2022·湖南·长郡中学模拟)(多选题)已知正方体的边长为2,M为的中点,P为侧面上的动点,且满足平面,则下列结论正确的是( )
A. B.平面
C.与所成角的余弦值为 D.动点P的轨迹长为
10.(2022·江苏淮安·模拟)(多选题)如图,已知正方体ABCD—的棱长为1,P为正方形底面ABCD内一动点,则下列结论正确的有( )
A.三棱锥-的体积为定值
B.存在点P,使得
C.若,则P点在正方形底面ABCD内的运动轨迹是线段AC
D.若点P是AD的中点,点Q是的中点,过P,Q作平面α垂直于平面,则平面α截正方体的截面周长为3
11.(2022·江苏·苏州市第六中学校三模)(多选题)某酒店大堂的壁灯的外观是将两个正三棱锥的底面重合构成的一个六面体(如图),已知,现已知三棱锥的高大于三棱锥的高,则( )
A.∥平面
B.二面角的余弦值小于
C.该六面体存在外接球
D.该六面体存在内切球
12.(2022·山东师范大学附中模拟)(多选题)已知正方体棱长为2,P为空间中一点.下列论述正确的是( )
A.若,则异面直线BP与所成角的余弦值为
B.若,三棱锥的体积为定值
C.若,有且仅有一个点P,使得平面
D.若,则异面直线BP和所成角取值范围是
13.(2022·福建漳州·三模)已知正方体ABCD—的棱长为4,M在棱上,且1,则直线BM与平面所成角的正弦值为___________.
14.(2022·北京西城·一模)如图,在棱长为的正方体中,点为棱的中点,点为底面内一点,给出下列三个论断:
①;②;③.
以其中的一个论断作为条件,另一个论断作为结论,写出一个正确的命题:___________.
15.(2022·重庆八中模拟)如图所示,是棱长为的正方体,、分别是下底面的棱、的中点,是上底面的棱上的一点,,过、、的平面交上底面于,在上,则异面直线与所成角的余弦值为___________.
16.(2022·浙江·湖州市菱湖中学模拟)已知正四面体VABC的棱长为2,E,F分别是棱VA,BC的中点,则该正四面体外接球的表面积为___________.异面直线BE与VF所成角的余弦值为___________.
第33练 椭圆-高考数学一轮复习小题多维练(新高考专用): 这是一份第33练 椭圆-高考数学一轮复习小题多维练(新高考专用),文件包含第33练椭圆-高考数学一轮复习小题多维练新高考专用解析版docx、第33练椭圆-高考数学一轮复习小题多维练新高考专用原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
第09练 函数的应用-高考数学一轮复习小题多维练(新高考专用): 这是一份第09练 函数的应用-高考数学一轮复习小题多维练(新高考专用),文件包含第09练函数的应用-高考数学一轮复习小题多维练新高考专用解析版docx、第09练函数的应用-高考数学一轮复习小题多维练新高考专用原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
专题13 导数及其应用-高考数学一轮复习小题多维练(新高考专用): 这是一份专题13 导数及其应用-高考数学一轮复习小题多维练(新高考专用),文件包含专题13导数及其应用-高考数学一轮复习小题多维练新高考专用解析版docx、专题13导数及其应用-高考数学一轮复习小题多维练新高考专用原卷版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。












