

2023乌鲁木齐第101中学高三下学期3月月考试题数学(文)含解析
展开乌鲁木齐市第101中学2022-2023学年
高三下学期三月月考 文科数学试题
总分150分 考试时间120分钟
一、单选题(共12小题每题5分共60分)
1.已知,,则( )
A. B.
C. D.
2.下列命题是真命题的有( )
A.有甲、乙、丙三种个体按的比例分层抽样调查,如果抽取的乙个体数为9,则样本容量为32
B.数据的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为,则这两组数据中较稳定的是甲
D.一组数的分位数为4
3.已知复数z满足(为虚数单位),则( )
A. B.5 C. D.2
4.某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C. D.
5.将函数的图象向右平移φ个单位,得到的图象关于原点对称,则φ的最小正值为( )
A. B.
C. D.
6.《易传·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化、阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数,若从阳数和阴数中各取一数,则其差的绝对值为3的概率为( )
A. B. C. D.
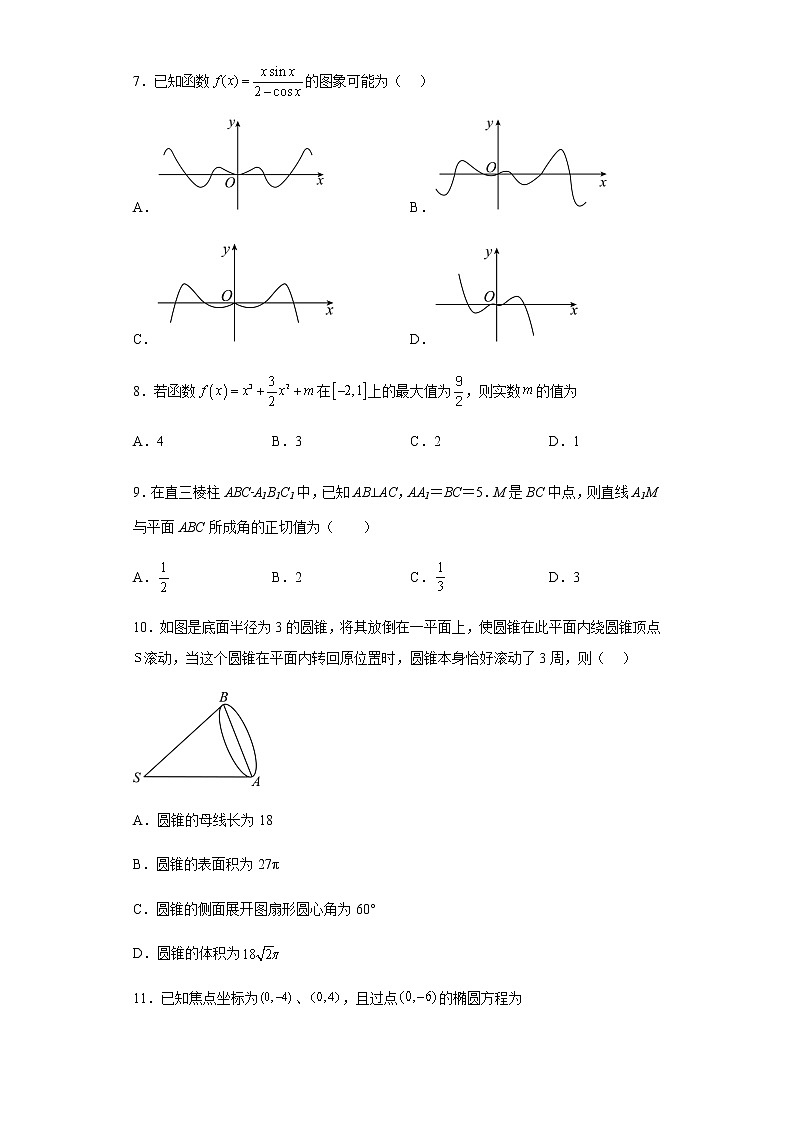
7.已知函数的图象可能为( )
A. B.
C. D.
8.若函数在上的最大值为,则实数的值为
A.4 B.3 C.2 D.1
9.在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AA1=BC=5.M是BC中点,则直线A1M与平面ABC所成角的正切值为( )
A. B.2 C. D.3
10.如图是底面半径为3的圆锥,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点滚动,当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了3周,则( )
A.圆锥的母线长为18
B.圆锥的表面积为27π
C.圆锥的侧面展开图扇形圆心角为60°
D.圆锥的体积为
11.已知焦点坐标为、,且过点的椭圆方程为
A. B.
C. D.
12.下列大小关系正确的是
A. B.
C. D.
二、填空题(共16分)
13.设,若,则实数的值等于__________.
14.设点在直线上,与轴相切,且经过点,则的半径为__________.
15.已知双曲线的两条渐近线与抛物线的准线分别交于两点,为坐标原点,若的面积为,则双曲线的离心率为______.
16.若,则的最大值是 .
三、解答题(共74分,请根据答题卡题号及分值在各题目的答题区域内作答,超出答题区域的答案无效。)
17.为加强素质教育,提升学生综合素养,立德中学为高一年级提供了“书法”和“剪纸”两门选修课.为了了解选择“书法”或“剪纸”是否与性别有关,调查了高一年级1500名学生的选择倾向,随机抽取了100人,统计选择两门课程人数如下表:
(1)补全列联表;
| 选书法 | 选剪纸 | 共计 |
男生 | 40 |
| 50 |
女生 |
|
|
|
共计 |
| 30 |
|
(2)依据小概率值的独立性检验,能否认为选择“书法”或“剪纸”与性别有关?
参考附表:
0.100 | 0.050 | 0.025 | |
2.706 | 3.841 | 5.024 |
参考公式:,其中.
18.已知正项数列的前项和为,且和满足:.
(1)求的通项公式;
(2)设数列,求的前项和.
19.如图所示,在长方体中,已知,.
(1)求:凸多面体的体积;
(2)若为线段的中点,求点到平面的距离;
(3)若点、分别在棱、上滑动,且线段的长恒等于,线段的中点为
①试证:点必落在过线段的中点且平行于底面的平面上;
②试求点的轨迹.
20.已知函数.
(1)若,求函数,的最小值;
(2)若在处的切线斜率与无关,求.
21.已知过点的直线与抛物线交于、两点,且,其中为坐标原点.
(1)求的值;
(2)当最小时,求直线的方程.
22.已知过抛物线的焦点的直线交抛物线于A,B两点,且,求AB所在的直线方程.
23.已知,,.
(1)若,求证:;
(2)若,求证:.
文科数学 月考答案解析:
1.A
【分析】由集合的并运算即可求解.
【解析】由题意得,,
故选:A.
2.B
【分析】根据分层抽样的定义计算可判断A;根据平均数、众数、中位数的定义判断B;根据方差公式计算乙组数据方差判断C;根据百分位数的定义判断D.
【解析】对A:甲、乙、丙三种个体按的比例分层抽样,故乙占了样本容量为,故A不正确;
对B:数据的平均数为,
众数为3,中位数为,故B正确;
对C:乙组数的平均数为,
方差为.
乙组数据更稳定,故C错误;
对D:将这组数据从小到大排列:1,2,2,3,
;又,则这组数据的分位数是第七个数与第八个数的平均数,为,故D错误.
故选:B.
3.A
【分析】由复数除法求得,再由复数模的定义求解.
【解析】由题意,
所以,
故选:A.
4.A
【分析】根据三视图,可知该图形是由一个圆锥和一个圆柱组合而成的,分别求出圆锥和圆柱的体积即可求出答案.
【解析】解:根据三视图,可知该图形是由一个圆锥和一个圆柱组合而成的,
圆锥的底面半径为2,高为2,
圆柱的地面半径为1,高为4,
所以圆锥的体积为,
圆柱的体积为,
所以该几何体的体积是.
故选:A.
5.A
【分析】求出平移后的解析式,得到,,求出φ的最小正值.
【解析】函数的图像向右平移个单位得到,
故,,解得:,,
当时,取得最小正值为,
故选:A.
6.C
【分析】根据古典概型的概率计算公式逐步求解即可.
【解析】因为阳数:1,3,5,7,9,阴数:2,4,6,8,10,所以从阳数和阴数中各取一数有:种,满足差的绝对值为3的有:,,,,,,共7种,则.
故选:C.
7.A
【解析】先利用判断出函数的奇偶性,再结合0右侧附近函数值的正负得到答案.
【解析】因为,所以为偶函数,
又,所以A选项正确.
故选:A.
8.C
【解析】试题分析:,由得,或.又,得.
考点:导数的应用.
9.B
【解析】根据平面,即可找到为直线与平面所成角,计算即可.
【解析】
因为平面,所以为直线与平面所成角.
在中,,,
.
故选
10.D
【分析】由题意可知,再利用圆锥的表面积公式,侧面积公式及体积公式,即可判断.
【解析】设圆锥的母线长为,以为圆心,为半径的圆的面积为,
又圆锥的侧面积,
因为圆锥在平面内转到原位置时,圆锥本身滚动了3周,
所以,解得,
所以圆锥的母线长为9,故选项A错误;
圆锥的表面积,故选项B错误;
因为圆锥的底面周长为,
设圆锥的侧面展开图扇形圆心角为,
则,解得,
所以圆锥的侧面展开图扇形圆心角为120°,故选项C错误;
圆锥的高,
所以圆锥的体积为,故选项D正确.
故选:D.
11.B
【分析】由椭圆焦点坐标,得到椭圆的焦点在轴,且,又由点,则,进而求得的值,即可得到椭圆的标准方程,得到答案.
【解析】由题意,椭圆焦点坐标为、,可得椭圆的焦点在轴,且,
又由过点,则,所以,
所以椭圆的标准方程为.
故选B.
12.A
【解析】∵,∴正确,故选A.
13.-5
【解析】由题意可得:,
结合向量垂直的充要条件可得:,
求解关于实数的方程可得:.
14.1或5##5或1
【分析】由点在直线上设, 圆与轴相切,
应用数形结合可得出与半径的关系,
再根据圆经过点也可写出与半径的关系,求解即可.
【解析】由点在直线上,设.
又与轴相切,且经过点,
半径,且.
解得或.则的半径为1或5.
故答案为: 1或5
15.2
【分析】求出双曲线的渐近线与准线的焦点坐标,利用的面积,找到的关系式,即可求出离心率.
【解析】因为双曲线的两条渐近线为,抛物线的准线为 ,所以 ,因为的面积为,
所以
故答案为:
16.
【解析】设,则,根据面积公式得,①
根据余弦定理得,,
将其代入①式得,
,
由三角形三边关系有,解得,
故当时,取得最大值
考点:解三角形
点评:主要是考查了三角形的面积公式的运用,属于基础题.
17.(1)列联表见解析
(2)能
【分析】(1)根据所给的数据补全列联表即可;
(2)计算卡方,再对比表中数据进行独立性检验即可
(1)
根据题意补全列联表,如下:
| 选书法 | 选剪纸 | 共计 |
男生 | 40 | 10 | 50 |
女生 | 30 | 20 | 50 |
共计 | 70 | 30 | 100 |
(2)
零假设为:选择“书法”或“剪纸”与性别无关.
根据列联表中数据,得,
根据小概率的独立性检验,推断不成立,即有95%的把握认为选“书法”或“剪纸”与性别有关.
18.(1)(2)
【分析】(1)先求出首项,对递推公式再递推一步,两个式子相减,最后可以判断出数列是等差数列,最后求出通项公式即可;
(2)利用错位相减法可以求出的前项和.
【解析】(1)当时,,解得:,
当且时,,
∴,
整理可得:,
∵,∴,∴,
∴数列以2为首项,4为公差的等差数列,
∴.
(2)由(1)知,,.
则,
∴.
19.(1)10;(2)(3)①证明见解析;②点的轨迹为以点M为圆心,为半径的圆在长方体内部的部分.
【分析】(1)根据多面体的体积是长方体的体积与三棱锥体积的差,可得解;
(2)由点M到平面的距离即为点到平面的距离,即为点A到直线BD的距离,由三角形的等面积法可求解;
(3)①由点P到底面ABCD的距离为定值,得点P必在过的中点M,且平行于底面ABCD的平面上;
②由, ,得点的轨迹为以点M为圆心, 为半径的圆在长方体内部的部分.
【解析】解:(1)因为多面体的体积是长方体的体积与三棱锥体积的差,
所以,
所以;
(2)因为点M到平面的距离即为点到平面的距离,即为点A到直线BD的距离,
所以过A作交于N,则由三角形的等面积法得,所以,所以,
于是点M到平面的距离为;
(3)①因为点P到底面ABCD的距离为定值,所以点P必在过的中点M,
且平行于底面ABCD的平面上;
②连接EA,由于, ,
所以点的轨迹为以点M为圆心, 为半径的圆在长方体内部的部分.
故得解.
20.(1)(2)
【分析】(1)求函数的导数,即求得单调区间,从而得到最小值,即可求得答案;
(2)在处的切线斜率与无关,即在处的值与无关,,即分析即的根,即可求得答案.
【解析】(1)当时,
在上单调递减,在上单调递增.
当时,最小值为
(2)
在处的切线斜率与无关
在处的值与无关;
令
在单调递减,在单调递增
当时,(小于趋于),且,
当时,与无关.
故.
21.(1);(2).
【分析】(1)设直线的方程为和抛物线方程联立利用韦达定理代入即可求得;(2)利用抛物线定义结合基本不等式求得取最小值时的值,代入点B坐标,将点代入,求得直线方程.
【解析】(1)设直线的方程为
,得
设,,所以,
因为,所以
又,所以,又因为,所以.
(2)根据抛物线定义,得,
所以,当且仅当时等号成立.
将代入,得(负值舍去).
将代入,得,即点
将点代入,得
所以直线的方程为,即.
22.或
【解析】试题分析:
求出抛物线的焦点坐标,判断直线的斜率是否存在,然后设出直线的方程,与抛物线方程联立消元后得到一元二次方程,根据根与系数的关系和弦长公式求得斜率即可.
试题解析:
由题意得抛物线的焦点为.
当直线的斜率不存在时,由条件可得,不合题意;
所以直线的斜率存在,设其方程为.
由消去x整理得,
∵直线与抛物线交于两点,
∴.
设,
则,
∴,
由条件得,
解得.满足.
∴直线的方程为或.
23.(1)证明见解析(2)证明见解析
【分析】(1)直接利用柯西不等式即可得证.
(2)直接利用三元基本不等式即可得证.
【解析】(1),当且仅当时等号成立,
所以成立;
(2)
又,,,,,,
所以,
则
,当且仅当,即,,时等号成立,
,即得证.
2023维吾尔自治区乌鲁木齐第101中学高三上学期11月月考数学试题含解析: 这是一份2023维吾尔自治区乌鲁木齐第101中学高三上学期11月月考数学试题含解析,文件包含新疆维吾尔自治区乌鲁木齐市第101中学2022-2023学年高三上学期11月月考数学试题含解析docx、新疆维吾尔自治区乌鲁木齐市第101中学2022-2023学年高三上学期11月月考数学试题无答案docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
2023届新疆乌鲁木齐市第101中学高三下学期2月月考数学(理)试题含解析: 这是一份2023届新疆乌鲁木齐市第101中学高三下学期2月月考数学(理)试题含解析,共18页。试卷主要包含了单选题,周四,填空题等内容,欢迎下载使用。
2023届新疆乌鲁木齐市第101中学高三下学期3月月考数学(理)试题含解析: 这是一份2023届新疆乌鲁木齐市第101中学高三下学期3月月考数学(理)试题含解析,共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












