山西大同市2021-2022中考数学一模试题分层-02图形的性质（基础题）

山西大同市2021-2022中考数学一模试题分层-02图形的性质（基础题）

一、单选题

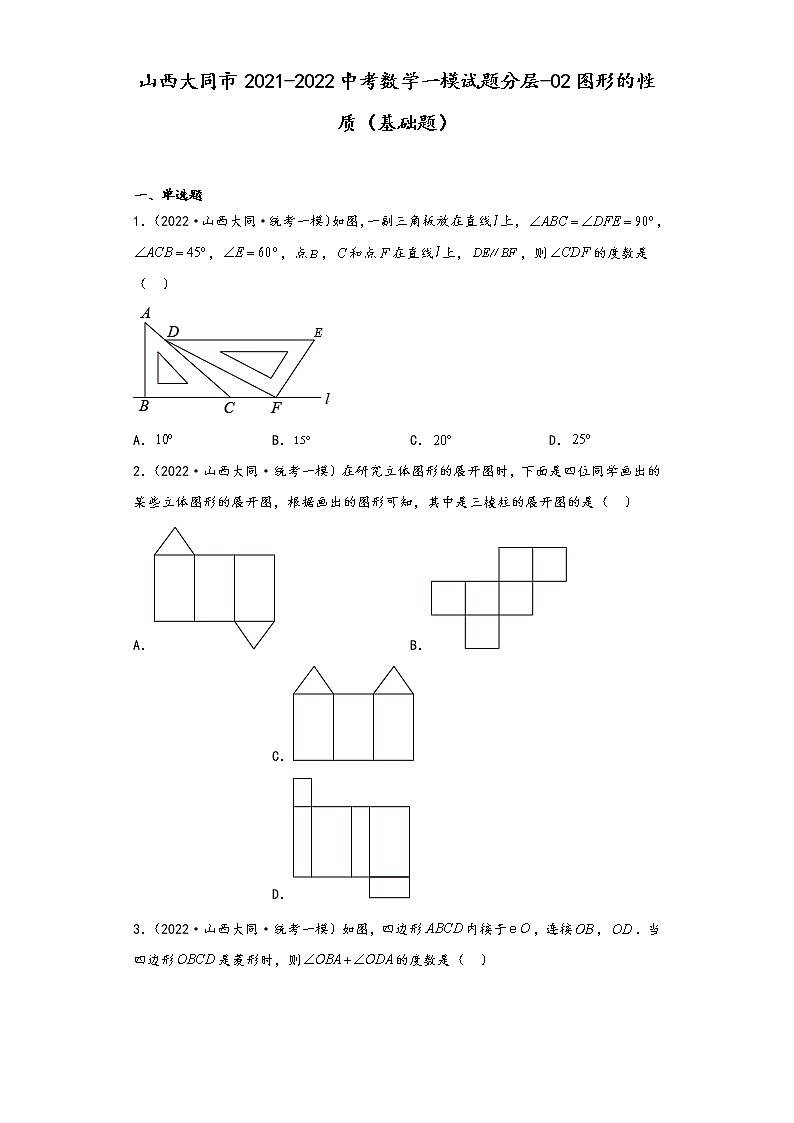
1．（2022·山西大同·统考一模）如图，一副三角板放在直线上，，，，点，和点在直线上，，则的度数是（    ）

A． B． C． D．

2．（2022·山西大同·统考一模）在研究立体图形的展开图时，下面是四位同学画出的某些立体图形的展开图，根据画出的图形可知，其中是三棱柱的展开图的是（    ）

A． B． C． D．

3．（2022·山西大同·统考一模）如图，四边形内接于，连接，．当四边形是菱形时，则的度数是（    ）

A． B． C． D．

4．（2022·山西大同·统考一模）如图，在中，，，，，点在上运动，连接，把沿折叠得到，交于点，，则图中阴影部分的面积是（    ）

A． B． C． D．

5．（2022·山西大同·校考一模）如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（　　）

A．10° B．20° C．25° D．30°

6．（2021·山西大同·统考一模）如图，点E，F分别在线段AB，CD上，连接BC交EF于点G，若AB//CD，∠1＝50°，∠2＝30°，则∠C的度数为（　　）

A．20° B．30° C．40° D．50°

7．（2021·山西大同·统考一模）如图，AB是半圆O的直径，AB＝10，以OB为边作平行四边形OBCE，若CE与半圆O相切于点C，则图中阴影部分的面积为（　　）

A． B． C． D．

二、填空题

8．（2022·山西大同·统考一模）如图，正方形的边长为3，连接对角线，以点为圆心，任意长为半径画弧交于点，与交于点，分别以点和为圆心，大于为半径作弧，两弧交于点，作射线交的延长线于点．过点作的垂线交的延长线于点，则的长为__________．

9．（2022·山西大同·统考一模）如图，在中，，，，在的内部作交边于点，，则的面积是__________．

10．（2022·山西大同·校考一模）在半径为2的⊙O中，弦AB为2，则弦AB所对的圆周角的度数为 ___．

11．（2022·山西大同·校考一模）如图，在中，．的半径为2，点是边上的动点，过点作的一条切线(点为切点)，则线段长的最小值为______．

12．（2021·山西大同·统考一模）若某个正多边形的每一个外角都等于其相邻内角的，则这个正多边形的边数是_____．

13．（2021·山西大同·统考一模）如图，在平面直角坐标系中，菱形ABCD的顶点A，B均在第一象限，D在x轴上，BC⊥x轴于点E，点E是BC的中点，若反比例函数的图象经过A，B两点，菱形ABCD的边长为2，则k的值为_____．

三、解答题

14．（2022·山西大同·统考一模）如图1是太原市新换的一批新能源公交车，图2，图3分别是该公交车双开门关闭、打开时的俯视示意图．、、是门轴的滑动轨道，，两门，的门轴，，，都在涓动轨道上，两门关闭时（图2），，分别在，处，门缝忽略不计（即，重合），两门同时开启，点，分别沿，的方向同时匀速滑动（如图3），当到达时，恰好到达，此时两门完全开启，在门开启的过程中，时，求的度数．

15．（2022·山西大同·统考一模）如图，是半圆的直径，圆心是，点在半圆上，连接，作弦，连接．过点作半圆的切线分别交，的延长线于点、．

(1)求证：；

(2)若，．求弦的长．

16．（2022·山西大同·统考一模）数学是一个不断思考，不断发现，不断归纳的过程，古希腊数学家帕普斯（Pappus，约300﹣350）把三等分的操作如下：

①以点为坐标原点，所在的直线为轴建立平面直角坐标系；

②在平面直角坐标系中，绘制反比例函数的图象，图象与的边交于点；

③以点为圆心，为半径作弧，交函数的图象于点；

④分别过点和作轴和轴的平行线，两线交于点，；

⑤作射线，交于点，得到．

(1)任务一：判断四边形的形状，并证明；

(2)任务二：请证明．

17．（2022·山西大同·统考一模）综合与探究

问题情境：

数学实践课上，老师要求同学们先制作一个透明的菱形塑料板，然后在纸上画一个与透明的菱形相似的菱形，把透明的菱形放在上面记作菱形，它们的锐角顶点重合，且，连接，．

(1)操作发现：

如图1，当边在边所在的射线上，直接写出与的数量关系：

(2)探究发现：

如图2，将菱形绕点按逆时针方向旋转，使点落在边上，连接和．你认为（1）中的结论是否还成立？若成立，请给出证明；若不成立，请说明理由；

(3)探究拓广：

如图3，在（2）的条件下，当时，探究并说明线段和的数量关系和位置关系．

18．（2022·山西大同·统考一模）综合与实践

如图，二次函数的图象与轴交于点和，点的坐标是，与轴交于点，点在抛物线上运动．

(1)求抛物线的表达式；

(2)如图2，当点在第四象限的抛物线上运动时，连接，，，当的面积最大时，求点的坐标及的最大面积；

(3)当点在轴上运动时，借助图1探究以点，，，为顶点的四边形是平行四边形，并直接写出点的坐标．

19．（2022·山西大同·校考一模）如图，为的直径，点在上，过点作的切线交的延长线于点，已知

(1)求的度数；

(2)若弦，垂足为，且，求图中阴影部分的面积．

20．（2022·山西大同·校考一模）如图1，在中，，，点为边的中点，直线经过点，过作，垂足为，过作，垂足为，连接、．

(1)当点、在直线的异侧时，延长交于点，猜想线段和的数量关系为______；

(2)如图2，直线绕点旋转，当点在直线的同侧时，延长交于点，（1）中的结论还成立吗？若成立，请给予证明：若不成立，请说明理由；

(3)直线绕点旋转一周的过程中，当线段的长度最大时，请判断四边形的形状为______，并求出它的面积为______．

21．（2021·山西大同·统考一模）如图，AB是⊙O的直径，C，D是圆上两点，，过D作⊙O的切线与AC的延长交于点E．判断△ADE的形状并说明理由．

22．（2021·山西大同·统考一模）阅读与思考

如图是小亮同学的数学日记，请仔细阅读，并完成相应的任务，

×年×月×目星期日

只用尺规也能判断两条线是否垂直

如图1，点是直线MN上一点，为射线，现在需要判断和是否垂直，然而我手头只有直尺和圆规，该怎么办呢？

我发现在初中三年的学习中很多知识都和直角有关，经过思考我想到了以下三个办法：

办法一：如图2，在射线上任取一点A，以A为圆心，大于长为半径作弧交于点B，点C，连接，若则，即．

办法二：如图3，在，上分别取点A，B，以AB为直径画圆，若点O在圆上，则．

办法三：如图4，在上任取一点A，以为边在作等边，延长交于点C，若，则，即．

还有只用尺规就可以判断和是否垂直的办法吗？……

任务：

（1）填空：“办法一”依据的数学定理是        ；“办法二”依据的数学定理是        ；

（2）请说明“办法三”尺规作图的合理性；

（3）在下图中再设计一种不同的方法探究与是否互相垂直（要求：尺规作图，保留作痕迹并描述探究的方法）

23．（2021·山西大同·统考一模）综合与实践

【问题情境】

在综合实践课上，老师让同学们以“顶角互补的等腰三角形纸片的图形变换”为主题开展数学活动．如图1，两张等腰三角形纸片ABC和AEF，其中AB＝AC＝m，AE＝AF＝n，m＞n，∠BAC＋∠EAF＝180°，△AEF绕点A顺时针旋转，旋转角为，点M为BF的中点．

【特例感知】

（1）如图1，当时，AM和CE的数量关系是       ；

（2）如图2，当时，连接AM，CE，请判断AM和CE的数量关系，并说明理由；

【深入探究】

（3）如图3，当为任意锐角时，连接AM，CE，探究AM和CE的数量关系，并说明理由；

【解决问题】

（4）如图4，△ABC和△AEF都是等腰直角三角形，∠BAC＝∠EAF＝90°，AB＝AC，AE＝AF，M为BF的中点，连接CE，MA，MA的延长线交CE于点N，若，，则AN＝      ．

参考答案：

1．B

【分析】根据可得，，在Rt△DEF中可得，即可求解．

【详解】解：∵，

∴．

在Rt△DEF中，，

∴，

∴．

故选：B．

【点睛】此题考查了平行线的性质以及直角三角形两锐角互余，解题的关键是掌握相关基础性质．

2．A

【分析】根据三棱柱的展开图底面均应是三角形直接判断即可．

【详解】解：根据题意，三棱柱的展开图的是图形A，

故选：A

【点睛】本题考查了立体图形的展开图，解题的关键是熟练掌握各立体图形的展开图．

3．B

【分析】由题意得，连接OA，OC，可知为等边三角形，可得出∠BAD=，根据圆的性质可知OB=OA=OD，∠ABO=∠BAO，∠ODA=∠OAD，即可求出结果．

【详解】解：如图，连接OA，OC，

∵四边形是菱形，

∴OB=BC，

∵OB=OC，

∴为等边三角形，

∴∠OBC=60°，

即：∠BOD=120°，

∴∠BAD=，

∵OB=OA=OD，

∴∠ABO=∠BAO，∠ODA=∠OAD，

∴．

故选：B．

【点睛】本题主要考查的是圆的基本性质，以及菱形的性质，熟练掌握圆中的基本性质是解题的关键．

4．D

【分析】过点A作，交BC于点F；延长，交BC于点G，设，根据勾股定理和等腰直角三角形的性质，通过列一元二次方程并求解，从而推导得AC和；设，根据轴对称、全等三角形和相似三角形的性质，分别计算得CD、AE，从而完成求解．

【详解】解：如图，过点A作，交BC于点F；延长，交BC于点G

设，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

∴，

∴或，

当时，，

，

∵，

∴不符合题意，故舍去；

当时，，

∴，

∵，

∴符合题意；

∴，

设，

∵把沿折叠得到，交于点，

∴，，

在和中，

，

∴，

∴，

∵，

∴，，

∴，

∴，即，

∴，

∴，

∵，，

∴，

∴，即，

∴，

∵，

∴，

∴图中阴影部分的面积，

故选：D．

【点睛】本题考查了轴对称、全等三角形、相似三角形、勾股定理、等腰直角三角形、一元二次方程的知识；解题的关键是熟练掌握轴对称、相似三角形、一元二次方程的性质，从而完成求解．

5．C

【详解】如图，延长AB交CF于E，

∵∠ACB=90°，∠A=30°，

∴∠ABC=60°．

∵∠1=35°，

∴∠AEC=∠ABC﹣∠1=25°．

∵GH//EF，

∴∠2=∠AEC=25°．

故选C．

6．A

【分析】根据平行线的性质求得∠EFD，然后利用三角形外角的性质求解．

【详解】解：∵AB//CD，

∴∠1=∠EFD＝50°

∴∠C=∠EFD-∠2=50°-30°=20°

故选：A．

【点睛】本题考查平行线的性质和三角形外角的性质，掌握相关性质正确推理计算是解题关键．

7．A

【分析】根据题目已知条件OB是⊙O的切线，利用切线的性质，连接OC，构造,又因为EC=CO,可得是等腰直角三角形，用等腰面积减去45°扇形面积即可求出答案．

【详解】

解：设OE与⊙O的交点为F；

如图，连接OC，

∵CE是⊙O的切线，

∴ ，

∵四边形OBCE为平行四边形，

∴,

∴∠COB=∠ECO=90°，∠EOC=∠OCB，

∵CO=OB,

∴∠OCB=45°，

∴∠EOC=45°，

∵ ,

∵S阴影=S△ECO-S扇形COF

= ,

故选：A．

【点睛】本题考查了切线的性质，扇形面积计算，等腰直角三角形的性质，利用切线的性质作辅助线，证明△ECO是等腰直角三角形是解题的关键．

8．

【分析】根据作图可知，BF为∠DBC的平分线，再结合，得出，从而得出，得到DB=DE，从而得出AE的长，利用勾股定理算出BE的长，最后根据得出EF的长即可．

【详解】根据作图可知，BE为∠DBC的平分线，

∴，

∵四边形ABCD为正方形，

，，，

，

∵，

∴，

∴，

∴DE=DB=，

∴，

∴，

∵，

∴，

，，

∴，

，

即．

故答案为：．

【点睛】本题主要考查了正方形的性质、三角形相似的判定和性质、勾股定理、等腰三角形的判定，根据题意得出是解题的关键．

9．54

【分析】过点D作DE⊥AB于E，可求△DEA是等腰直角三角形，DE=AE=AD∙sin∠BAD=，设BE=x，由△BED∽△BCA可得，求得x的值，因△BED∽△BCA，BC>AC得，BE=，勾股定理得到BD的值，进一步求得面积即可．

【详解】解：过点D作DE⊥AB于E，如图，

∵∠ACB=90°，AC=6，CD=3

在Rt△ACD中，

又∵∠BAD=45°，DE⊥AB

∴△DEA是等腰直角三角形

∴DE=AE=AD∙sin∠BAD=

设BE=x

∴AB=BE+EA=x+

在Rt△BDE中，

又∵∠DBE=∠ABC，∠BED=∠BCA=90°

∴△BED∽△BCA

∴

即

∴

解得，，

∵△BED∽△BCA

又∵BC>AC

∴

∴BE>ED=

∴BE=

则

∴BC=BD+DC=18>AC=6

∴，符合题意

若，不符合题意舍去

故答案为：54．

【点睛】本题考查了相似三角形的判定与性质、勾股定理、锐角三角函数、一元二次方程，解题的关键是通过相似三角形的性质求出BE的值．

10．30°或150°

【分析】弦所对的弧有优弧和劣弧，故弦所对的圆周角也有两个，它们的关系是互补关系；弦长等于半径时，弦所对的圆心角为60°，进而即可求解．

【详解】解：如图，弦AB所对的圆周角为∠C，∠D，

连接OA、OB，

因为AB＝OA＝OB＝2，

所以，∠AOB＝60°，

根据圆周角定理知，∠C＝∠AOB＝30°，

根据圆内接四边形的性质可知，∠D＝180°−∠C＝150°，

所以，弦AB所对的圆周角的度数30°或150°．

故答案是：30°或150°．

【点睛】若圆中的一条弦等于圆的半径，则此弦和两条半径构成了等边三角形；在圆中，弦所对的圆周角有两个，不要漏解．

11．

【分析】连接，根据勾股定理知，可得当时，即线段最短，然后由勾股定理即可求得答案．

【详解】连接．

∵是⊙的切线，

∴；

∴，

∴当时，线段OP最短，

∴PQ的长最短，

∵在中，，

∴，

∴，

∴．

故答案为．

【点睛】本题考查了切线的性质、等腰直角三角形的性质以及勾股定理．此题难度适中，注意掌握辅助线的作法，得到时，线段最短是关键．

12．8

【分析】根据每个外角都等于相邻内角的，并且外角与相邻的内角互补，就可求出外角的度数；根据外角度数就可求得边数．

【详解】解：设外角是x度，则相邻的内角是3x度．

根据题意得：x+3x＝180，

解得x＝45．

则多边形的边数是：360°÷45°＝8．

故答案为：8．

【点睛】本题考查了多边形的内角和与外角和的知识．此题难度不大，注意掌握方程思想的应用是解题关键．

13．

【分析】设A（x，2），根据菱形的性质和勾股定理求得CE=BE=1，DE=，则B（x+，1），进而由A、B坐标即可求出k的值．

【详解】解：∵菱形ABCD的边长为2，

∴AD=DC=BC=2，AD∥BC，

∵点E为BC的中点，

∴BE=CE=1，

∵BC⊥x轴，

∴AD⊥x轴，

在Rt△DEC中，DC=2，CE=1，

由勾股定理得DE= =，

设A（x，2），则B（x+，1），

∵反比例函数的图象经过A，B两点，

∴2x= x+，解得：x= ，

∴k=2 ，

故答案为：2 ．

【点睛】本题考查菱形的性质、反比例函数的图象与性质、平行线的性质、勾股定理、坐标与图形，熟练掌握菱形的性质和反比例函数的性质是解答的关键．

14．

【分析】由题设条件可得Rt△AEB≌Rt△DFC，进而可得线段之间的倍数关系，在三角形中，根据锐角三角函数值，可求得角的度数．

【详解】解：∵点，分别沿，的方向匀速滑动，当到达时，恰好到达，

∴．

∵，

在和中，

，

∴．

∴．

∵，

∴．

∵，

∴．

∴在中，．

∴．

∴的度数是．

【点睛】本题是数学知识在实际生活中的应用，准确理解题意，选择用到的数学知识进行解答是解题的关键．

15．(1)见解析

(2)

【分析】（1）连接OC，如图，先证明OC∥AF，再根据切线的性质得OC⊥EF，从而得到AF⊥EF；

（2）先利用OC∥AF得到∠COE=∠DAB，在Rt△OCE中，利用余弦的定义得到，解得OB=4，连接BD，如图，根据圆周角定理得到∠ADB=90°，然后根据余弦的定义可计算出AD的长．

（1）

证明：如图，连接，和，和交于点．

∵过点作半圆的切线交的延长线于点，

∴．

∴．

∵，

∴．

∴．

∵，

∴．

∴．

∵是半圆的直径，

∴．

∴．

∴．

∴．

（2）

解：∵，

∴．

∵，，

∴在中，．

∴．

∵，，

∴．

∴．

∵是半圆的直径，

∴，∠ADB=90°

∴在中，．

∴．

∴．

∴弦的长是．

【点睛】本题主要考查了圆周角定理，切线的性质，解直角三角形，掌握圆周角定理，切线的性质，解直角三角形是解题的关键．

16．(1)矩形，证明见解析

(2)见解析

【分析】（1）根据题意可知，，，由此即可证明四边形是矩形；

（2）先证明，则，再由．推出．推出．即可得到．则．

（1）

解： 结论：四边形是矩形．

证明：∵分别过点和作轴和轴的平行线，两线交于点，，

∴，，．

∴四边形是平行四边形．

∵，

∴四边形是矩形．

（2）

证明：∵矩形的对角线与相交于点，

∴，，．

∴．

∴．

∵是的外角，

∴．

∵以点为圆心，为半径作弧，交函数的图象于点，

∴．

∴．

∴．

∵，

∴．

∴．

∴．

【点睛】本题主要考查了矩形的性质与判定，坐标与图形，反比例函数与几何综合，等腰三角形的性质与判定，三角形外角的性质等等，正确理解题意是解题的关键．

17．(1)，理由见解析

(2)成立，理由见解析

(3)，，理由见解析

【分析】（1）只需要利用SAS证明△BAE≌△DAG即可得到BE=DG；

（2）同（1）求解即可；

（3）如图，延长与的延长线交于点，证明，得到，，则．再证明．即可得到．

（1）

解：，理由如下：

∵四边形ABCD和四边形AEFG都是菱形，

∴AB=AD，AE=AG，

又∵∠BAE=∠DAG，

∴△BAE≌△DAG（SAS），

∴BE=DG；

（2）

解：（1）中结论成立，理由如下：

证明：∵四边形和四边形是菱形，

∴，．

∵，

∴．

∴．

在和中，

，

∴．

∴．

（3）

解：，，理由如下：

理由如下：如图，延长与的延长线交于点．

∵四边形和四边形是菱形，，

∴菱形和菱形是正方形．

∴，，，．

∴，．

∴．

在和中，

，

∴．

∴，．

∴．

∵，

∴．

∴．

在中，．

∴．

【点睛】本题主要考查了菱形的性质，全等三角形的性质与判定，三角形内角和定理等等，熟知菱形的性质和全等三角形的性质与判定是解题的关键．

18．(1)

(2)，6

(3)，，，

【分析】（1）根据待定系数法即可求得抛物线的表达式；

（2）连接，过点作轴，作轴，设点的坐标是，然后根据表示出的面积，然后利用利用二次函数的性质即可求得结果；

（3）根据题意，设点的坐标为：（a，0），点的坐标是．由以点，，，为顶点的四边形是平行四边形，根据中点坐标公式分三种情况：①当BC为对角线时，②当BD为对角线时，③当BE为对角线时，列出方程，即可求得结果．

（1）

解：点和点代入二次函数，

得：

解得．

∴抛物线的表达式是．

（2）

解：如图，连接，过点作轴，作轴．

设点的坐标是．

∴，．

∵，，

∴，．

∴

．

∵，

∴当时，的面积最大且为6．

当时，．

∴点的坐标是，的最大面积是6．

（3）

解：∵点在轴上，

∴设点的坐标为：（a，0），点的坐标是．

∵以点，，，为顶点的四边形是平行四边形，

①当BC为对角线时，由中点公式可得

解得：，

点的坐标为：（4，0）时与点重合，应舍去，

此时，点的坐标为：（1，0）；

②当BD为对角线时，由中点公式可得

解得：，

点的坐标为：（4，0）时与点重合，应舍去，

③当BE为对角线时，由中点公式可得

解得：，

此时，点的坐标为：（，0），（，0）；

综上所述，点的坐标为：（1，0），（7，0），（，0），（，0）．

【点睛】本题主要考查了求二次函数的解析式、图形面积的求法、平行四边形的性质、二次函数的应用等，综合性强、难度较大，熟练应用二次函数模型求三角形面积的最大值是解题的关键．

19．(1)

(2)

【分析】（1）连接OC，则△OCD是直角三角形，可求出∠COD的度数；由于∠A与∠COD是同弧所对的圆周角与圆心角．根据圆周角定理即可求得∠A的度数；

（2）由图可知：阴影部分的面积是扇形OCB和Rt△OEC的面积差；那么解决问题的关键是求出半径和OE的长；在Rt△OCE中，∠OCE=∠D=30°，已知了CE的长，通过解直角三角形，即可求出OC、OE的长，由此得解．

(1)

解：（1）连接OC，

∵CD切⊙O于点C，

∴∠OCD=90°，

∵∠D=30°，

∴∠COD=60°，

∵OA=OC，

∴∠A=∠ACO=30°；

(2)

解：∵CF⊥直径AB，，

∴CE=，

∴在Rt△OCE中，tan∠COE= ， OE=，

∴OC=2OE=4 ，

∴S扇形BOC=，S△EOC＝，

∴S阴影=S扇形BOC-S△EOC=．

【点睛】本题主要考查了切线的性质、垂径定理以及扇形面积的计算方法．不规则图形的面积，可以转化为几个规则图形的面积的和或差来求．

20．(1)PF=EG

(2)成立，理由见解析

(3)矩形，2

【分析】（1）证△PBE≌△PCG（AAS），得PE=PG，再由直角三角形斜边上的中线性质即可得出结论；

（2）延长EP交FC的延长线于G，同（1）得△PBE≌△PCG（AAS），得PE=PG，再由直角三角形斜边上的中线性质即可得出结论；

（3）连接AP，由等腰三角形的性质得∠APC=90°=∠CFA，设线段AC的中点为M，得点P、F都在以线段AC为直径的圆上，当PF=AC=2时，PF取得最大值，此时四边形APCF是正方形，则四边形BEFC是矩形，即可求解．

(1)

解：PF=EG，理由如下：

∵BE⊥a，CF⊥a，

∴，

∴∠PBE=∠PCG，∠PEB=∠PGC，

∵点P为BC边的中点，

∴PB=PC，

∴△PBE≌△PCG（AAS），

∴PE=PG，

∵CF⊥a，

∴∠EFG=90°，

∴PF=EG， 故答案为：PF=EG；

(2)

解：（1）中的结论还成立，

证明如下： 延长EP交FC的延长线于G，如图所示：

同（1）得：△PBE≌△PCG（AAS），

∴PE=PG，

∵CF⊥a，

∴∠EFG=90°，

∴PF= EG；

(3)

解：连接AP，如图所示：

∵AB=AC，点P为BC边的中点，

∴BP=CP，AP⊥BC，

∴∠APC=90°， 设线段AC的中点为M，

∵CF⊥a， ∴∠CFA=90°，

∴点P、F都在以线段AC为直径的圆上，

当PF=AC=2时，PF取得最大值，此时四边形APCF是正方形，

则四边形BEFC是矩形，AF=，

∴四边形BEFC的面积=2正方形APCF的面积=2×AF2=2×2=4．

【点睛】本题是四边形综合题目，考查了矩形的判定、正方形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质、直角三角形斜边上的中线性质、平行线的判定与性质，圆的基本性质等知识；本题综合性强，熟练掌握等腰直角三角形的性质和直角三角形斜边上的中线性质，证明三角形全等是解题的关键，属于中考常考题型．

21．△ADE为直角三角形．理由见解析．

【分析】根据同圆中相等的弧所对的圆周角相等，得出∠EAD=∠DAB，连接OD，由圆的切线性质可得∠EDO=90°，即∠EDA+∠ADO=90°，再由∠DAO=∠ADO，等量代换出∠EAD=∠ADO，即可求出∠E=90°．

【详解】△ADE为直角三角形．理由如下：

如图，连接OD，

∵DE与⊙O相切于点D，

∴DE⊥OD，

∴∠ADO＋∠ADE＝90°

∵，

∴∠CAD＝∠DAO．

∵OA＝OD，

∴∠OAD＝∠ODA，

∴∠CAD＝∠ODA，

∴∠CAD＋∠ADE＝90°．

在△ADE中，∠CAD＋∠ADE＋∠AED＝180°

∴∠AED＝90°，

∴△ADE为直角三角形．

【点睛】本题考查了同圆中相等的弧所对的圆周角相等，切线的性质，解题关键是利用切线的性质得出垂直关系．

22．（1）等腰三角形三线合一；直径所对的圆周角是直角；（2）见解析；（3）答案不唯一，作图及描述见解析．

【分析】（1）第一空：利用等腰三角形三线合一；第二空：根据直径所对的圆周角是直角，可以判断；

（2）根据等边三角形及等腰三角形的性质，利用等量代换，可以证明；

（3）可以利用全等三角形的判定及性质来证明．

【详解】（1）“办法一”依据的数学定理是：等腰三角形三线合一，

“办法二”依据的数学定理是：直径所对的圆周角是直角；

（2）∵是等边三角形，

,

，

，

是的一个外角，

，

，

，

即．

（3）答案不唯一，如：

以为圆心，任意长为半径作弧，交与B，C两点，在上任取一点A，若，则，即．

【点睛】本题考查来如何证明两条直线垂直的多种方法，解题的关键是：回顾与直角有关的知识来证明．

23．（1）；（2），理由见解析；（3），理由见解析；（4）．

【分析】（1）利用等腰三角形两腰相等和M为中点，得到，，，则可推出两线段的数量关系；

（2）利用已知条件求出∠BAF＝90°，再根据直角三角形斜边上的中线等于斜边的一半，推出，再证明，即可得到；

（3）添加辅助线，延长AM至点G，使得MG＝AM．利用对角相互相平分得到ABGF是平行四边形，利用角的关系推出∠AFG＝∠CAE，再证明，即可得到；

（4）与（3）中添加辅助线的方法相同，延长AM至点G，使得MG＝AM．利用对角相互相平分得到ABGF是平行四边形，则．利用角的关系推出，证明得到，则，，又因为，所以，进而推出．又，则．由和即可求出的值．

【详解】（1）∵两张等腰三角形纸片ABC和AEF，其中AB＝AC，AE＝AF

∴，

又∵点M为BF的中点

∴

∴

∴

（2）

理由：∵∠BAC＋∠EAF＝180°，∠CAE＝90°，

∴∠BAF＝90°．

∵在Rt△BAF中，∠BAF＝90°，M是BF的中点，

在△ACE和△ABF中

．

．

．

（3）．

理由：如图，延长AM至点G，使得MG＝AM．

∵M是BF的中点，

∴BM＝FM．

又∵MG＝AM，

∴四边形ABGF是平行四边形

∴AC＝AB＝FG，AB//GF．

∴∠BAF＋∠AFG＝180°．

∵∠BAC＋∠EAF＝180°，

∴∠BAF＋∠CAE＝180°．

∴∠AFG＝∠CAE．

在△ACE和△FGA中

．

．

．

（4）如图所示，延长AM至点G，使得，连接、．

∵M是BF的中点，

∴BM＝FM．

又∵MG＝AM，

∴四边形ABGF是平行四边形

∴AC＝AB＝FG，AB//GF， ．

∴∠BAF＋∠AFG＝180°．

∵∠BAC＋∠EAF＝180°，

∴∠BAF＋∠CAE＝180°．

∴∠AFG＝∠CAE．

在△ACE和△FGA中

．

，，．

，

∴．

又∵

∴，

∴，

∴．

∴

∴．

【点睛】本题是与四边形相关的综合性题目，主要考查平行四边形的性质和判定，全等三角形的性质和判定，以及旋转，直角三角形斜边上的直线等于斜边的一半等相关知识．