

2022-2023学年广东省梅州市平远县河头中学九年级(下)开学数学试卷(含解析)
展开2022-2023学年广东省梅州市平远县河头中学九年级(下)开学数学试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
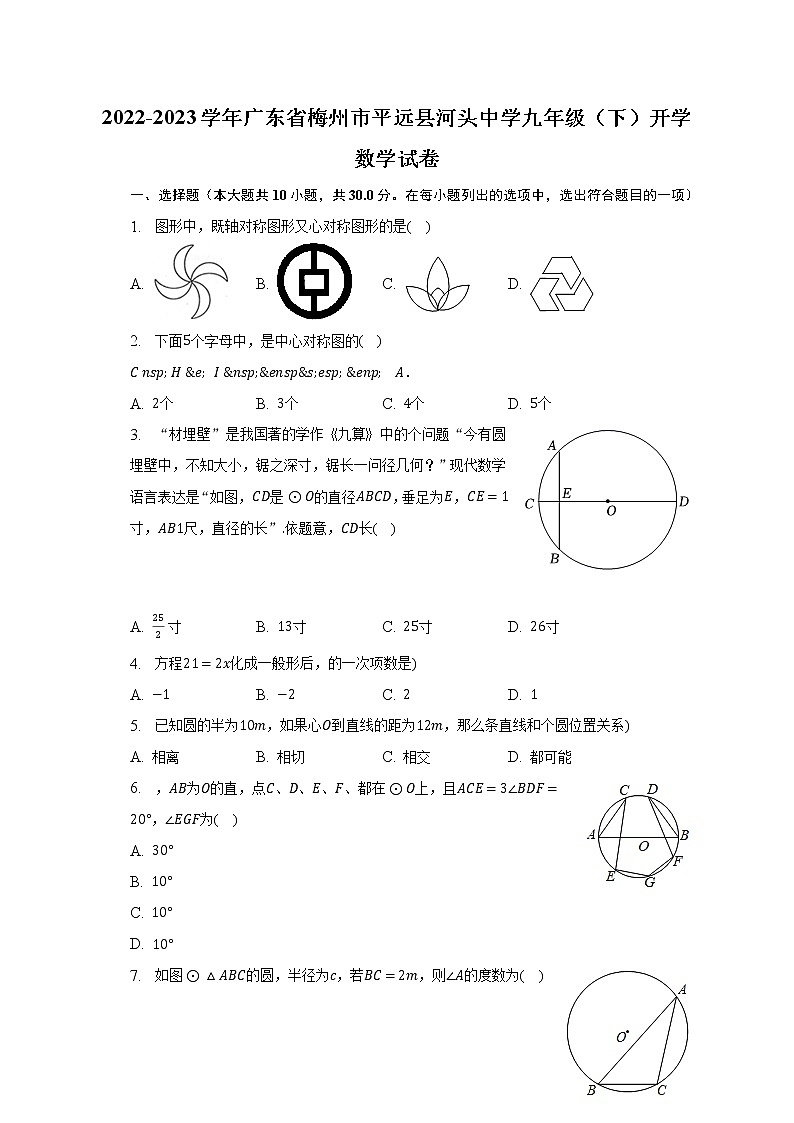
1. 图形中,既轴对称图形又心对称图形的是( )
A. B. C. D.
2. 下面个字母中,是中心对称图的( )
.
A. 个 B. 个 C. 个 D. 个
3. “材埋壁”是我国著的学作九算中的个问题“今有圆埋壁中,不知大小,锯之深寸,锯长一问径几何?”现代数学语言表达是“如图,是的直径,垂足为,寸,尺,直径的长”依题意,长( )
A. 寸 B. 寸 C. 寸 D. 寸
4. 方程化成一般形后,的一次项数是
A. B. C. D.
5. 已知圆的半为,如果心到直线的距为,那么条直线和个圆位置关系
A. 相离 B. 相切 C. 相交 D. 都可能
6. ,为的直,点、、、、都在上,且,为( )
A.
B.
C.
D.
7. 如图的圆,半径为,若,则的度数为( )
A.
B.
C.
D.
8. 如将抛物线向上平移单位长度,得到的抛物线的表达是
A. B. C. D.
9. 用证证明:中,、、不能有两个角是钝时,假,、、中有两个是钝令,,则所结论与列四选项相矛盾的( )
A. 已知 B. 三角形内和等于
C. 钝角三形的定义 D. 上结论都不对
10. 函数的部象所示,象点,对称轴为直线下列结论:若点点、点在该数图象,则若方的两根为和,且,则;其中正的结论有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共7小题,共28.0分)
11. 二次函数,当时,随的增大而 填增大”或减小”
12. 方程的为 .
13. 在半径为的圆中,挖去个径为圆面剩下一圆环积则与的函数关系式为 其中自变量的值范围是 .
14. 已知点是物线的图象的点.
过点作于点,以为斜边和,使得,则的最小值为 ;
15. 如图抛物线经过平得到抛物:,抛线对称轴与两段抛物线所围成影部分的面积是 .
16. 章算术国代著名数著作,书中载:“有圆,埋在壁中,不知大小以锯,深一,道长一尺问径几何?”用学语言可表述为“如图,的直径弦于寸,寸,求直径长”则 寸
17. 如图所示从高为的点处向右上抛一个小球,小球路线呈物形,小球过时达到最大高,后在下台阶上弹起,,小球弹形一条与形状同抛物线,且点与,在同一直线,则小起时最大高度是
三、解答题(本大题共8小题,共65.0分。解答应写出文字说明,证明过程或演算步骤)
18. 本小题分
有完全相同的小球,把们分为,,,在一袋中,随机地摸出一个小球放回,再机地摸出一个小.
求出的两个球号码之和等的概率.
19. 本小题分
小明在上学的路上要过多路口每个路口都设有红、黄三号灯,假设在各路口遇号相互独立的如果有个路口,求小明学路上到二路口时一次遇红灯的概率请用“画树状图”或“表等方写出分析过
20. 本小题分
个口袋中放有球,红球个,白球和球各若个,每个球除了颜色以外有任何别取出的一个是白色,它在桌上,闭上眼睛从中余下的再任意取出一个球,取出红的概率是多少?
21. 本小题分
已知次三式,圆同其进行变形如:
圆的答确吗?果不正确,写出正确的解答.
22. 本小题分
若关方程有根,求的取值围.
23. 本小题分
已是的二函数,求出它的解式.
24. 本小题分
如图,正的边长,、分别是边上点,且,将绕点逆时针旋转,得到若,求的长.
25. 本小题分
如图,当,求;
图,在中,,,,不动,绕点连接、,为的中点,连接.
答案和解析
1.【答案】
【解析】解:是中心对称图形;既是对称图又是中心对称;是对称图形;既是轴称图又不是中心对图形.
故选:
观察四个选中的图形,找出既是轴对称图形是中对称图形那个得出结.
题考查心称图形以及轴对称图形记轴对称及中心称图形的特点解题的关键.
2.【答案】
【解析】解:不是中心对称形,
所以,是称图形的有、、共个字母.
不是中心称形,
中心称图形,
是中心对形,
故选:
根据中心图形概念对各字母分析判断可解.
本题考查了对图形的念:中心对称图形是寻对中心,旋转度后与原图合.
3.【答案】
【解析】解:连,
在直角中,,寸,
,
则寸,
解得,
圆径是寸,尺寸,
故选:
连接,圆的径是,在角中,,,在直角中勾股定即可列方求得半径,进而求得直径的长.
题考垂径定理和股定理,正确作辅助线是解题关键.
4.【答案】
【解析】解:方程化成一般形式为,一次项数是.
故选:
一元二次方程的般形式,是常数且其中,,分别叫次数,一次项数,常项.据此作答.
本考了一元二的一形式:是常数且特别要意的条件.这是在做题程中容忽视的点.在一般形式中二次项,次项,是常数项.其中,分叫二项系数,一次项系数,常.
5.【答案】
【解析】解:半径为,
圆心到一条直线的距离为,
故选:
根据圆心到直线的距离大于的半,则直和相离.
本题考查了直线和圆位置关和数量的关系:时,直线和圆相离.
6.【答案】
【解析】解:如图,接,.
,
,
是径,
,
,
故选:
利用圆周角理求出,再用圆内接四边形的对角互性求解即可.
本考周角定理圆内接四边形性质等识解题的关键是学添加常用线,灵活运用所学知识解决问题.
7.【答案】
【解析】解:连接和,
为等边三角,
,
,
,
故选:
连接和,证明为等三,得到的度,再利用圆周角定理出.
本题考查了圆角定和等边三的判定和性质,解题的关是确的作辅助线.
8.【答案】
【解析】解:将抛物线上平个位得到的物线表达式是.
故选:
根据函数图左加右减得答案.
本考查了图象与几何变换,用平规律“左加右减,上加下减”代入函数式求得平移后的函解析式.
9.【答案】
【解析】解:假设、、中两个角是钝,
这与三角内角和等相矛,
则,
故选:
根据反证的一般步骤判即.
本查的是反证法的用证法的一般骤是:假设命题的结论不成立从假设出,经过推理论证,出;由判定假设不正确,从而肯定原命题的结论正确.
10.【答案】
【解析】解:由题意可知:称轴,
由,
程的根为和,
,正确;
由于图可:直线与抛物线有交,
当时,,此时大值,
故正确;
,误;
直线的对称点为,
设,,
,故正;
,
,
故选:
根据二函的图与性质即可出答案.
本考查二次函数的象,题的关键是练运用次函数的图象与性,本题于等题型.
11.【答案】减小
【解析】解:在直角标系中画出二函数的示意图如下:
当,即在对称轴的左,的增而减小,
故答案:减小.
利用二次数的解式出意图,根图象解答即可.
本题主考了二次函数的质,结数的图象利用数形结合的思想答单明了.
12.【答案】或
【解析】解:,
则
,
,
故答案为:或.
利用因式分法求可得.
本题主考查解元二次方程能力,熟练握解元二方程的几常用方法:直接开平方法、因式分解法、式法、配方法,结合程特择适、简方法是解题的键.
13.【答案】
【解析】解:半径为的圆的面积为,径为的圆的面积为:,则函析式:且.
根据圆环的面积半径的圆的面积半径为的的面积线段,应大于,不能外圆的径,可得量的取围.
根据题意,找到所量等量关系是问题的关键.应注据实际义得变量的取值范围.
14.【答案】
【解析】解:当函数为.
当点在顶处短,
的最为,
,
轴于点,
,
,
抛物线的顶点坐标为,.
是点纵坐,
最小值,
,
答案为:.
利用方法将抛物线解转化为顶点式,可以直得答案;
易证得四形是矩形,根据矩形性得到当最小最小,根抛物最小值即求得经过.
考了待数法求二次函数解,二次函数图象的质,二数的最值,证得四边是矩形解的关键.
15.【答案】
【解析】解:抛物线:的顶点标为,
当时,
平后抛物线顶点标为,对称轴为直,
平移后阴影部分面积等于图三角形的面为:,
故答案为:.
确定出物线的点坐标然后求出物线对称与原抛物的交坐标,从判断出阴影分面积等于三角的面积,再根据三角形面公式列式算即得解.
本题考查了二函数图象几变换确定与阴部分面积相等的三形是解题关键.
16.【答案】
【解析】解:设的半径为寸,则寸寸,
解得,
寸,
直径的长寸.
在中,
故答案为.
连接,设的半径为寸,则寸,寸先根据径理得寸,再利勾股定理得然解方程出从而得直长.
本题考了径定理的应把垂径定理勾股定理结合,构造角角,可解决计算弦长、半径、弦心距等题.
17.【答案】
【解析】解:如图以点为原点,在直轴所在直线为轴建立直角坐标,
,
抛物线顶点为,,
解得,
把点代入,,得,
小球起时的最大度为
抛物线的对称轴为线,
,
弹起后的抛物线的解析式为,
与点关于称轴称的点为在平台上,
,
设析式为,
则,,,,,,,
,
故案为:.
以原所在直线为轴,在直线轴建立直角坐标系,则,,,,分别求出出时物线的解析式,直的解析式;刻求出第次小球落台阶时点的坐标及点的坐,进求弹起后抛物线的析式,则可得论.
本题属于二次函数的用,考查了二函数的质,定系数法识,解题的关键是学会寻特殊点解.
18.【答案】解:据题意,可以画出如下树形:
设个号码和等于为事件 ,
从树形图可以出,两次摸球出现的所有可结种.
出的个球号码之等的概率为.
【解析】画状图列举出所情况;
出的两个球号码和等于情况数除以总情数即为所的概率.
本题考查借助树状图或列表法求概率.果个事有种可能,而且这些件的可性相,中事件现结果,那么的概率.
19.【答案】解:画状图为:
明在上学路上到第二路口时第一遇到红灯的概率.
【解析】画树状展示所有种可能结果数,再找明在上学路到第二个路口时第一次遇红灯的结果数然后据概公式求.
题查列表法树状图法:利用列表或树状图法展示所等能的果,再选出符事件或的结果数目,然后利用率公计算事件或事的概率.
20.【答案】解:由于球的数目减少了个,故总减小为,所以取球概率加了,变为,
故答为:.
【解析】让红球个除以剩余球的总数,即为求概率.
考查用频率估概量反复试验下频率定值即概率.用到的知识点概所求情数与总情况数之比.部分的具体数目体数目率.
21.【答案】解:圆圆的解答误.
,
所以当,这个二次三项式有最小为.
【解析】由可知圆圆的解答错根据配方的题步骤改写为再用非负数的性质求解.
题考的应用配方法理论据是公式这里次项系数不是,所以需要先提出二次项系数,使得二次项系数变为然后一次项系数一半的方.考查了非的性质.
22.【答案】解:若,则方程为,显然方程有解;
,,
上,.
【解析】分和分别求,其中是利用判别式列出等式,解之可.
本题主要考查根判式,一元二次方程的根与有如关:
时,方程两个相的两实数根;
当,方无实数根.
23.【答案】解:根据次函数定义可得,且,
当,;
解得或;
上所述,该次函数解析式为:.
【解析】据二次函数定义可得,,之得的值,而可得数解析式.
本题要考查二次函数的定义,根据二次数定义得出关于方,解之得出的值是的关.
24.【答案】解:逆时针旋转得到,
,且,
,
,
在中,勾股定理得,
,
,
,,
,
≌,
、、三共,
在中,,
,
解得,
.
【解析】由旋可得,为角,得,,得为可出再由,利用可得三角形与三角全等,由全等三角对应边相可得出;可得到正方形的边长为,求出的长再由求出的长,设,得出在三角形,利用股定理列出关于的方程,求出方程的解到的,即为的长.
此题考查了正方形的质,旋转的质,全等三角形的判定与性质,以及勾股定理.此题度中,注意握后的应关系,注意掌握数结合思想方思的应.
25.【答案】,
,
,
,
.
,
,
,
证明如图,
,
≌
≌,
,
在中,为的中点,
,,
在与中
成立,
.
【解析】为直角形中线,所以然通过≌即可求得.
长交在上取,证≌从而证得,然根据三角形的中位线等于底边的半,求,即求得.
考查三角形等的判定和性质等腰三性质,三角形中位的性质等.作出正确的辅线是解题关键
2022-2023学年广东省梅州市平远县七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年广东省梅州市平远县七年级(下)期中数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年广东省梅州市五华县华东中学九年级(下)开学数学试卷(含解析): 这是一份2022-2023学年广东省梅州市五华县华东中学九年级(下)开学数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省梅州市平远县铁民中学八年级(下)开学数学试卷(含解析): 这是一份2022-2023学年广东省梅州市平远县铁民中学八年级(下)开学数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












