【全套】中考卷数学复习专题（知识梳理+含答案）-动点问题专题训练

这是一份【全套】中考卷数学复习专题（知识梳理+含答案）-动点问题专题训练，共14页。
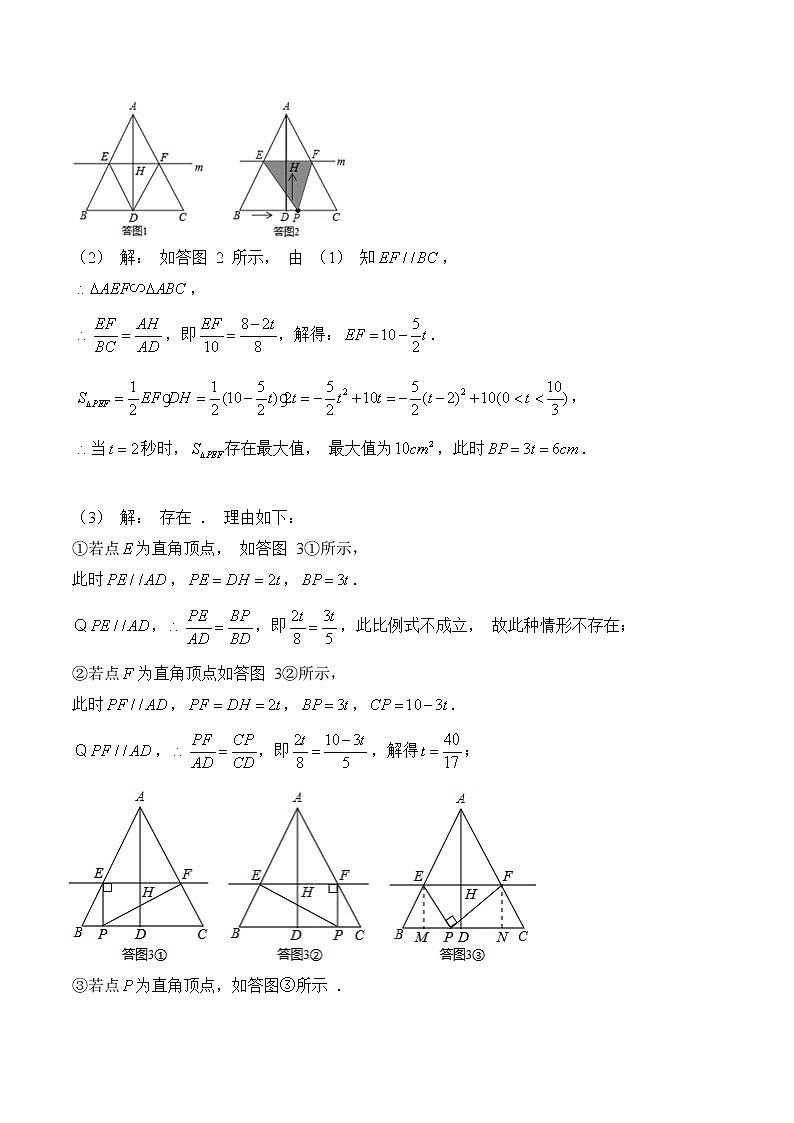
 中考专题训练 动点问题 例1.              如图， 在中，，于点，，． 点从点出发， 在线段上以每秒的速度向点匀速运动， 与此同时， 垂直于的直线从底边出发， 以每秒的速度沿方向匀速平移， 分别交、、于、、，当点到达点时， 点与直线同时停止运动， 设运动时间为秒．（1） 当时， 连接、，求证： 四边形为菱形；（2） 在整个运动过程中， 所形成的的面积存在最大值， 当的面积最大时， 求线段的长；（3） 是否存在某一时刻，使为直角三角形？若存在， 请求出此时刻的值；若不存在， 请说明理由 ．【解答】（1） 证明： 当时，，则为的中点， 如答图 1 所示 ．又，为的垂直平分线，，．，于点，，．，，，，，，即四边形为菱形 ．（2） 解： 如答图 2 所示， 由 （1） 知，，，即，解得：．，当秒时，存在最大值， 最大值为，此时． （3） 解： 存在 ． 理由如下：①若点为直角顶点， 如答图 3①所示，此时，，．，，即，此比例式不成立， 故此种情形不存在；②若点为直角顶点如答图 3②所示，此时，，，．，，即，解得；③若点为直角顶点，如答图③所示 ．过点作于点，过点作于点，则，．，，即，解得，．在中， 由勾股定理得：．，，即，解得，．在中， 由勾股定理得：．在中， 由勾股定理得：，即：化简得：，解得：或（舍 去）．综上所述， 当秒或秒时，为直角三角形 ．
例2.              如图， 在同一平面上， 两块斜边相等的直角三角板和拼在一起， 使斜边完全重合， 且顶点，分别在的两旁，，，（1） 填空：　　，　   　（2） 点，分别从点，点同时以每秒的速度等速出发， 且分别在，上沿，方向运动， 当点运动到点时，、两点同时停止运动， 连接，求当、点运动了秒时， 点到的距离 （用 含的式子表示）（3） 在 （2） 的条件下， 取中点，连接，，设的面积为，在整个运动过程中，的面积存在最大值， 请求出的最大值 ．（参考数据，【解答】解： （1），，，，，，；故答案为：，；（2） 过点作于，作，交的延长线于，如图所示：则，，，，，，，，，，，，点到的距离为；（3），，为的中点，，，的面积梯形的面积的面积的面积，即是的二次函数，，有最大值，当时，有最大值为．
例3.              如图，是正方形的对角线，，边在其所在的直线上平移， 将通过平移得到的线段记为，连接、，并过点作，垂足为，连接、．（1） 请直接写出线段在平移过程中， 四边形是什么四边形？（2） 请判断、之间的数量关系和位置关系， 并加以证明；（3） 在平移变换过程中， 设，，求与之间的函数关系式， 并求出的最大值 ．【解答】（1） 四边形为平行四边形；（2），，理由如下：四边形是正方形，，，，，，，在和中， ，，，，；（3） 如图， 过作于．①如图 1 ，当点在点右侧时，则，，，即，又，当时，有最大值为 2 ；②如图 2 ，当点在点左侧时，则，，，即，又，当时，有最大值为；综上所述，当时，有最大值为 2 ． 例4.              如图， 在平面直角坐标系中，为原点， 四边形是矩形， 点，的坐标分别是和，，点是对角线上一动点 （不 与，重合） ，连结，作，交轴于点，以线段，为邻边作矩形．（1） 填空： 点的坐标为　，　；（2） 是否存在这样的点，使得是等腰三角形？若存在， 请求出的长度；若不存在， 请说明理由；（3）①求证：；②设，矩形的面积为，求关于的函数关系式 （可 利用①的结论） ，并求出的最小值 ．【解答】解： （1）四边形是矩形，，，，，．故答案为，． （2） 存在 ． 理由如下：，，，，①如图 1 中， 当在线段上时，是等腰三角形， 观察图象可知， 只有，，，是等边三角形，，在中，，，，．当时，是等腰三角形 ．②如图 2 中， 当在的延长线上时，是等腰三角形， 只有，，，，综上所述， 满足条件的的值为 2 或． （3）①如图 1 ，过点作交于，交于，和，，直线的解析式为，设，，，，，，，，． ②如图 2 中， 作于．在中，，，，，，在中，，，矩形的面积为，即，，，时，有最小值． 例5.              已知，，，斜边，将绕点顺时针旋转，如图 1 ，连接．（1） 填空：　 60 　；（2） 如图 1 ，连接，作，垂足为，求的长度；（3） 如图 2 ，点，同时从点出发， 在边上运动，沿路径匀速运动，沿路径匀速运动， 当两点相遇时运动停止， 已知点的运动速度为 1.5 单位秒， 点的运动速度为 1 单位秒， 设运动时间为秒，的面积为，求当为何值时取得最大值？最大值为多少？【解答】解： （1） 由旋转性质可知：，，是等边三角形，．故答案为 60 ． （2） 如图 1 中， ，，，，，是等边三角形，，，，． （3）①当时，在上运动，在上运动， 此时过点作且交于点．则，，．时，有最大值， 最大值． ②当时，在上运动，在上运动 ．作于． 则，，．当时，取最大值，， ③当时，、都在上运动， 作于．，，，当时，有最大值， 最大值，综上所述，有最大值， 最大值为．