


数学八年级下册第九章 图形的相似9 利用位似放缩图形说课ppt课件
展开1. 前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
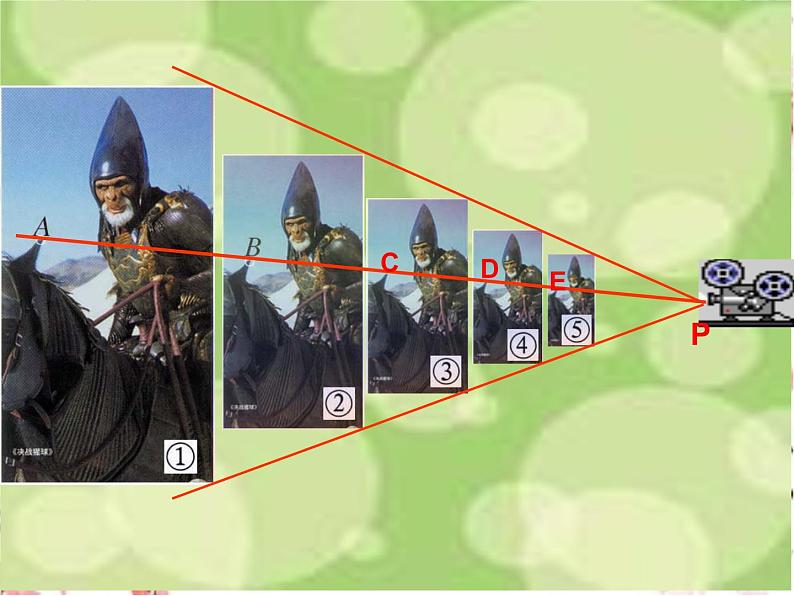
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
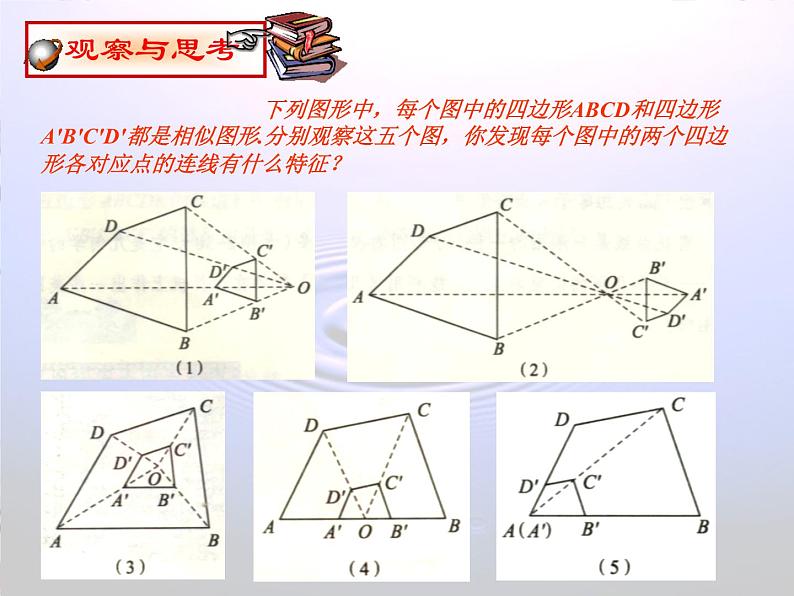
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
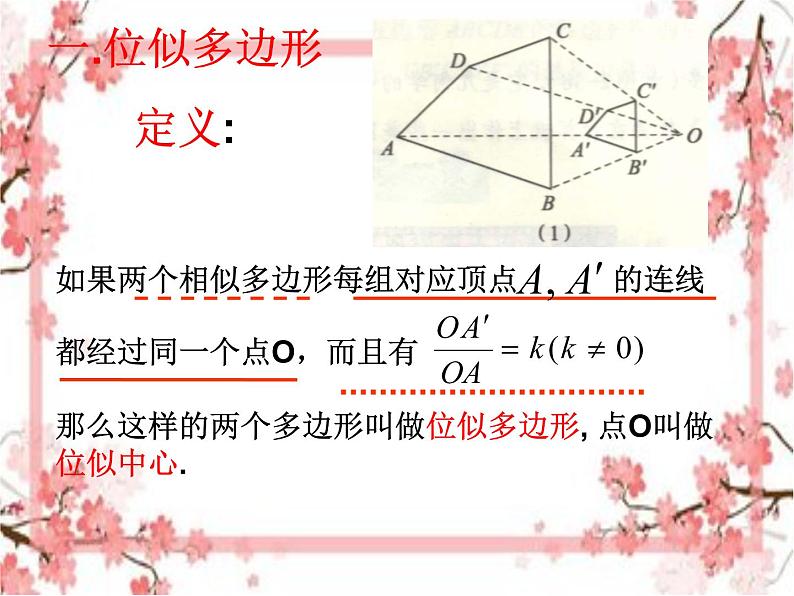
如果两个相似多边形每组对应顶点 的连线都经过同一个点O,而且有 那么这样的两个多边形叫做位似多边形, 点O叫做位似中心.
1.定义即判断方法:以下三条件缺一不可.
(2)每组对应顶点所在直线都经过同一点.
(3)每组对应顶点到交点的距离的比值相等
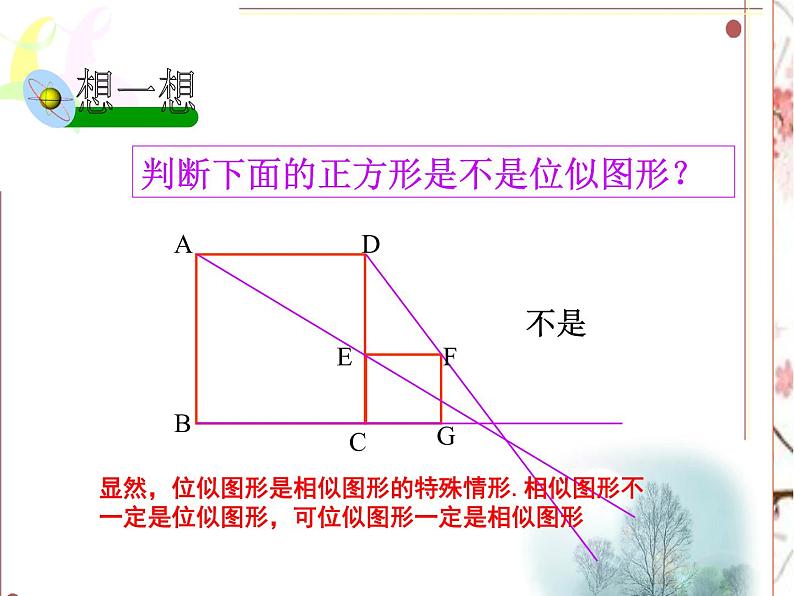
判断下面的正方形是不是位似图形?
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
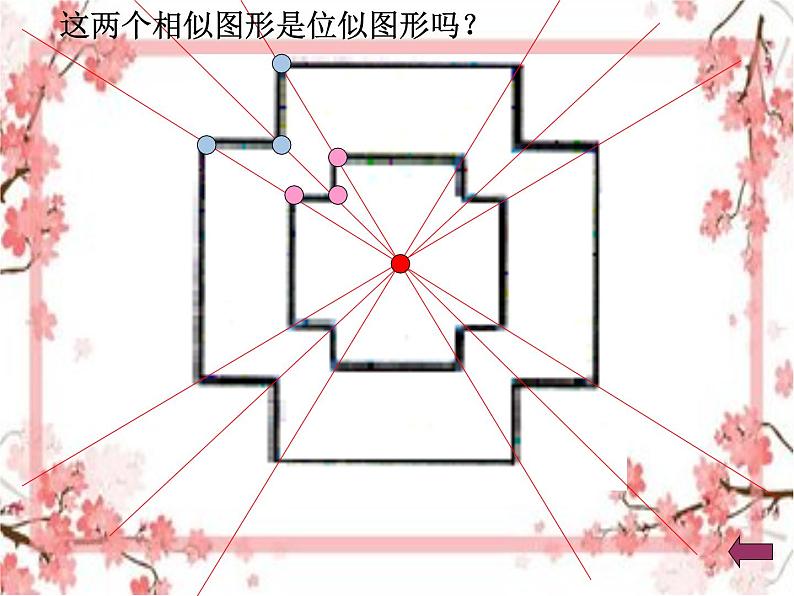
这两个相似图形是位似图形吗?
. 判断下列各对多边形是不是位似多边形.
1.正五边形ABCDE与正五边形A′B′C′D′E′;
2. 相似△ABC与△ A′B′C′.
3、判断下列各对图形哪些是位似图形,哪些不是. 为什么?
2.两个位似多边形的对应边有什么位置关系?为什么?
3.位似多边形一定是相似多边形吗?反过来呢?
位似多边形一定是相似多边形,相似多边形不一定是位似多边形,
4.观察下图中的五个图,位似图形的位似中心与这两个图形有什么位置关系?
两个图形可以在位似中心的同侧或异侧,位似中心可以在图形内还可以在一个图形的边上或顶点.
2. 位似多边形定义即性质
(2)位似多边形上任意一对对应点到位似中心的距离之比等于相似比.
(3)位似多边形中的对应线段平行(或在一条直线上).
(1)位似多边形是相似多边形,
你能作出下列位似图形的位似中心吗?:
二.利用位似放缩图形
如图,已知△ABC和点O.以O为位似中心,画△ABC的位似图形,使它△ABC的相似比为2.
如何对一个图形进行放大或缩小呢?
2.如果位似中心在三角形内部呢?
1.用上面的方法画出的三角形为何与△ABC相似?
第一步:在原图上找若干个关键点,并任取一点作为位似中心。第二步:作位似中心与各关键点连线。第三步:在连线上取关键点的对应点,使之满足放缩比例。第四步:顺次连接截取点。
利用作位似图形的方法,你能将下面的三角形缩小,使缩小后的三角形与原三角形对应线段的比为1 : 2 吗?试一试。
将黄色五角星缩小为原来的一半
作位似图形,要用尺规作图:1、若指定位似中心,一般可作两个, 位于位似中心两侧;2、若不指定位似中心,一般可作无数个。
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在图所示的图案中,你能找到这些变换吗?
鲁教版 (五四制)八年级下册2 矩形的性质与判定说课课件ppt: 这是一份鲁教版 (五四制)八年级下册2 矩形的性质与判定说课课件ppt,共12页。PPT课件主要包含了矩形的四个角都是直角,对角线,矩形的性质,知识回顾,矩形的判定方法,教学目标,例题引领,当堂达标,见导学案等内容,欢迎下载使用。
数学八年级下册2 矩形的性质与判定图片ppt课件: 这是一份数学八年级下册2 矩形的性质与判定图片ppt课件,共14页。PPT课件主要包含了矩形的性质,知识回顾,教学目标,定义判定,∠A900,四边形ABCD是矩形,矩形的定义,几何语言,合作探究,你能证明上述结论吗等内容,欢迎下载使用。
鲁教版 (五四制)八年级下册2 矩形的性质与判定备课课件ppt: 这是一份鲁教版 (五四制)八年级下册2 矩形的性质与判定备课课件ppt,共13页。PPT课件主要包含了对边平行且相等,对角相等且邻角互补,互相平分,复习导入,教学目标,合作探究,一般性质,特殊性质,自主探究1,比一比知关系等内容,欢迎下载使用。













