数学1.2 向量的基本关系图片ppt课件

这是一份数学1.2 向量的基本关系图片ppt课件，共25页。PPT课件主要包含了新知探究，存在夹角，初步应用，课堂练习，作业布置，目标检测，∵AB∥CD，∴A正确等内容，欢迎下载使用。

向量集数与形于一身，有着极其丰富的实际背景，在现实生活中随处可见的位移、速度、力等既有大小又有方向的量都是它的物理背景，有向线段是它的几何背景．向量就是从这些实际对象中抽象概括出来的数学概念．
由平面内的所有向量可以构成一个平面内的向量集合，和研究一般的集合一样，我们常常要研究这个集合中的特殊元素，以及它们之间的关系，这是我们本节的任务．
问题1　前面我们已经学习了平面向量的概念、表示方法及两个特殊向量，请你回忆一下形成这些平面向量相关概念的基本方法和途径是什么？
以鲜明的表象（力、速度、位移等）作为过渡，
在鲜活的感知、抽象的过程中经历概念的抽象、概括和符号化的过程．
认识到向量的两个本质属性（大小和方向）；
用实数中的特殊数0与1，类比得到向量中长度为0的向量（零向量），
长度为1的向量（单位向量）这两个特殊向量．
问题2　任意两个单位向量都相等吗？
单位向量的模相同，但方向不一定相同．
线段与线段间有数量关系（等与不等），还有位置关系（平行、重合、相交）．
向量与向量之间有关系．
问题3　类比线段与线段间的基本关系，我们自然会提出这样的问题：向量与向量之间有没有“关系”呢？如果有，这种新的关系又是什么呢？
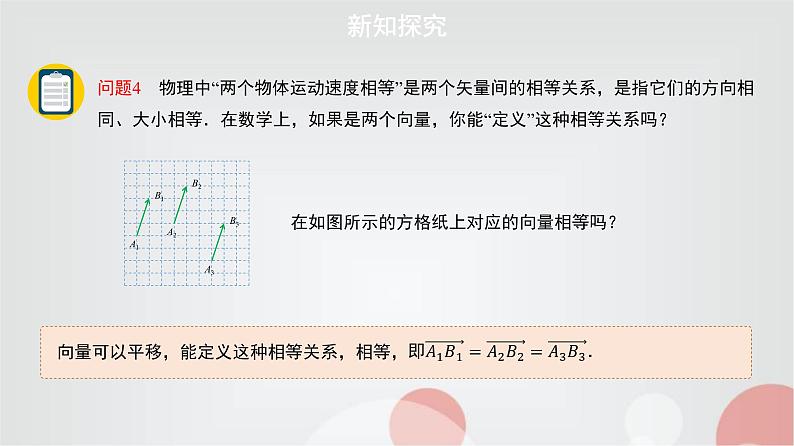
向量可以平移，能定义这种相等关系，相等，
问题4　物理中“两个物体运动速度相等”是两个矢量间的相等关系，是指它们的方向相同、大小相等．在数学上，如果是两个向量，你能“定义”这种相等关系吗？
在如图所示的方格纸上对应的向量相等吗？
问题5　若两个有向线段方向相同、长度相等，则它们表示的向量相等吗？若相等，那么代表相等向量的有向线段与起点位置有关吗？请举例说明．
它们表示的向量相等，且与有向线段的起点无关．
问题6　你能给相等向量下一个定义吗？
长度相等且方向相同的向量，叫做相等向量．
向量a与b相等，记作a＝b．
又表示它们的有向线段在同一直线上，所以两向量共线．
问题8　你能给出共线向量的定义吗？零向量与哪一个向量共线？
两个非零向量a，b的方向相同或相反，称这两个向量为共线向量或平行向量．
规定：零向量与任一向量共线．
也称这两个向量共线或平行，记作a∥b．
问题9　若a∥b，b∥c，那么一定有a∥c吗？
因为当b＝0时，a，c可以是任意向量．
不相同，由相等向量定义可知，向量可以任意移动．
由于任意一组平行向量都可以移动到同一直线上，
因此共线向量所在的直线可以平行，也可以重合．
所以平行向量也叫做共线向量．
问题10　如图所示，在△OAB中，OA⊥AB，向量c与向量a是否共线？向量a和向量b相等吗？它们之间形成了怎样的特殊关系？特殊之处是什么？
图中向量c与向量a不共线，
向量a和向量b不相等，
因为OA⊥AB，所以向量a和向量b垂直，
特殊之处在于向量a和向量b所成的角是90°．
向量的夹角与直线的夹角不一样，向量的夹角与向量的方向有关．
问题11　平面中的任意两个向量都可以平移至起点，它们存在夹角吗？若存在，向量的夹角与直线的夹角一样吗？
问题12　你能说出向量的夹角情况吗？
则θ＝∠AOB（0°≤θ≤180°）称为向量a与b的夹角．
当θ＝0°时，a与b同向；
当θ＝180°时，a与b反向；
当θ＝90°时，a与b垂直，记为：a⊥b．
规定：零向量与任一向量垂直，即对于任意向量a，都有0⊥a．
例1　如图，点D，E，F分别是等边三角形ABC的三边AB，BC，AC的中点．在以点A，B，C，D，E，F为起点或终点的向量中：
例2　一辆汽车从A点出发向西行驶了100千米到达B点，然后又改变方向向西偏北50°走了200千米到达C点，最后又改变方向，向东行驶了100千米到达D点．
四边形ABCD为平行四边形，
练习：教科书第83页练习1，2，3，4，5．
作业：教科书第78页，A组4，5，6．
如图，等腰梯形ABCD中，对角线AC与BD交于点P，点E，F分别在两腰AD，BC上，EF过点P，且EF∥AB，则（　　）
设点O是正方形ABCD的中心，则下列结论错误的是（　　）
∵B，O，D三点在一条直线上，