

湘教版初中数学七年级下册期末测试卷(困难)(含答案解析)
展开第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 小杨在商店购买了a件甲种商品,b件乙种商品,共用213元,已知甲种商品每件5元,乙种商品每件19元,那么a+b的最大值是
( )
A. 37B. 27C. 23D. 20
2. 商家常将单价不同的A、B两种糖混合成“什锦糖”出售,记“什锦糖”的单价为:A、B两种糖的总价与A、B两种糖的总质量的比.现有两种“什锦糖”:一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖甲,另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖乙.若B种糖比A种糖的单价贵40元/千克,“什锦糖”甲比“什锦糖”乙的单价贵5元/千克,则A种糖的单价为( )
A. 50元/千克B. 60元/千克C. 70元/千克D. 80元/千克
3. 已知实数x、y、z满足x2+y2+z2=4,则(2x−y)2+(2y−z)2+(2z−x)2的最大值是( )
A. 12B. 20C. 28D. 36
4. 设a,b是实数,定义@的一种运算如下:a@b=(a+b)2−(a−b)2 ,则下列结论:①若a@b =0,则a=0或b=0;②a@(b+c)= a@b+ a@c ; ③不存在实数a,b,满足a@b=a2+5b2;④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.其中正确的是. ( )
A. ②③④B. ①③④C. ①②④D. ①②③
5. 设681×2019−681×2018=a,2015×2016−2013×2018=b,6782+1358+690+678=c,则a,b,c的大小关系是( )
A. b
A. 3(ax2+8axy+16ay2)B. 3a(x+4y)2
C. 3a(x+16y)2D. 3a(x2+8xy+16y2)
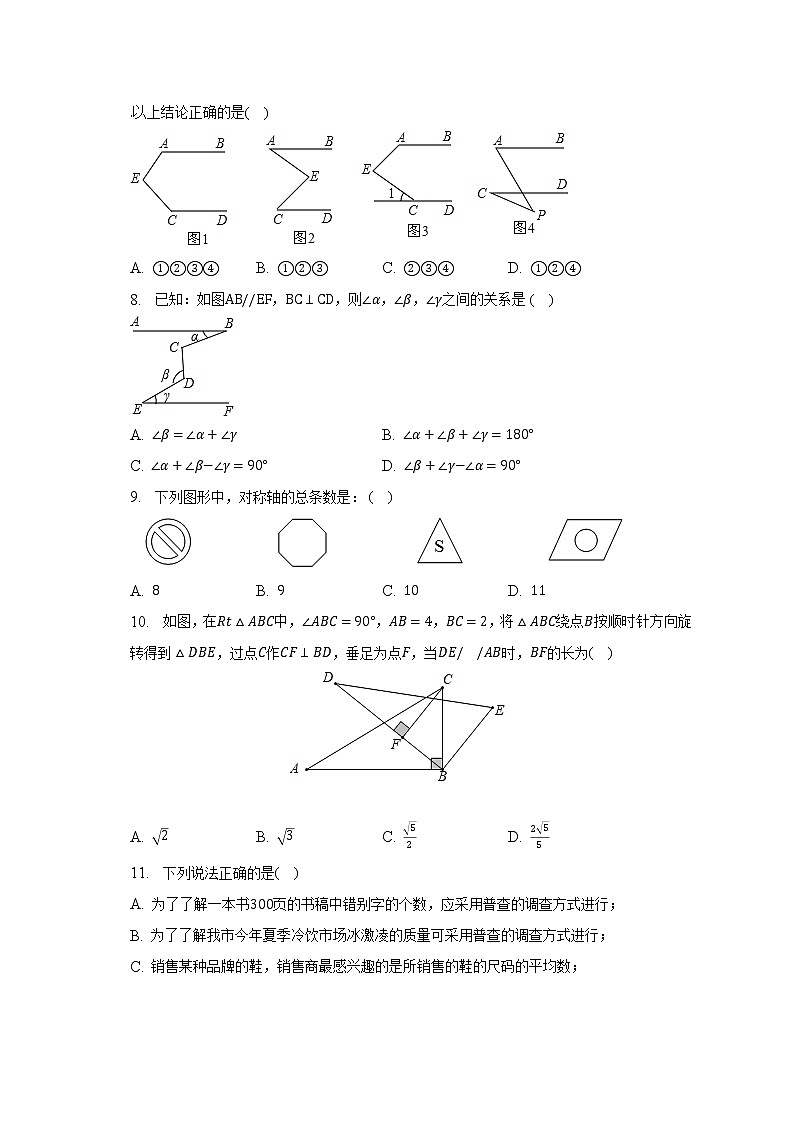
7. ①如图1,AB//CD,则∠A+∠E+∠C=180°;②如图2,AB//CD,则∠E=∠A+∠C;③如图3,AB//CD,则∠A+∠E−∠1=180°;④如图4,AB//CD,则∠A=∠C+∠P.以上结论正确的是( )
A. ①②③④B. ①②③C. ②③④D. ①②④
8. 已知:如图AB//EF,BC⊥CD,则∠α,∠β,∠γ之间的关系是( )
A. ∠β=∠α+∠γB. ∠α+∠β+∠γ=180°
C. ∠α+∠β−∠γ=90°D. ∠β+∠γ−∠α=90°
9. 下列图形中,对称轴的总条数是:( )
A. 8B. 9C. 10D. 11
10. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,将△ABC绕点B按顺时针方向旋转得到△DBE,过点C作CF⊥BD,垂足为点F,当DE//AB时,BF的长为( )
A. 2B. 3C. 52D. 255
11. 下列说法正确的是( )
A. 为了了解一本书300页的书稿中错别字的个数,应采用普查的调查方式进行;
B. 为了了解我市今年夏季冷饮市场冰激凌的质量可采用普查的调查方式进行;
C. 销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的平均数;
D. 为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取1000份试卷进行统计分析,在这个问题中,样本是被抽取的1000名学生;
12. 如下图是根据某班40名同学一周的体育锻炼情况绘制的统计图,该班40名同学一周参加体育锻炼时间的中位数,众数分别是( )
A. 10.5,16B. 8.5,16C. 8.5,8D. 9,8
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 2023年是中国农历癸卯(兔)年。某商场推出“鸿福兔”、“吉祥兔”两种限量礼盒,每种礼盒均装有紫色、白色、红色三种颜色的兔公仔,每一种礼盒的成本是该礼盒中所有兔公仔的成本之和(包装费用不计).其中,“鸿福兔”礼盒分别装有3个紫色,1个白色,1个红色兔公仔,“吉祥兔”礼盒分别装有2个紫色,3个白色,3个红色兔公仔.每个“鸿福兔”礼盒中所有兔公仔的成本之和为1个紫色兔公仔的5倍,每个“吉祥兔”礼盒的利润率为50%,且每个“吉祥兔”礼盒的售价比每个“鸿福兔”礼盒高20%.店庆当天销售这两种礼盒的总销售额为60万元,总利润率为60%,则这天销售“鸿福兔”礼盒的总利润是____万元.
14. 如果4x2−(a+1)x+9是一个完全平方式,则a的值是_____
15. 如图,直线EF上有两点A、C,分别引两条射线AB 、CD . ∠DCF=60°,∠EAB=70°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD与AB平行所有满足条件的时间t=_____.
16. 数据1,4,6,9,a,其中整数a是这组数据的中位数,则该组数据的平均数是______.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车m辆,B型车n辆,一次运完,且恰好每辆车都装满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案,且分别求出m,n的值;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
18. (本小题8.0分)
甲、乙两个同时解方程组ax+5y=15, ①4x−by=−2, ②甲看错了方程 ①中的a,得到方程组的解为x=−3,y=−1,乙看错了方程 ②中的b,得到方程组的解为x=5,y=4,试计算a2017+(−110b)2016
的值.
19. (本小题8.0分)
已知13x2−6xy+y2−4x+1=0,求(x+y)13·x10的值.
20. (本小题8.0分)
利用我们学过的知识,可以推导出下面这种形式的优美等式:a2+b2+c2−ab−ac−bc=12[(a−b)2+(b−c)2+(c−a)2],该等式从左到右的变形中,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
(1)请你检验这个等式的正确性;
(2)若a=2014,b=2015,c=2016,你能很快求出a2+b2+c2−ab−ac−bc的值吗?
21. (本小题8.0分)
材料一:对于个位数字不为零的任意三位数M,将其个位数字与百位数字对调得到M′,则称M′为M的“倒序数”,将一个数与它的“倒序数”的差的绝对值与99的商记为F(M).
例如523为325的“倒序数”,F(325)=|325−523|99=2;
材料二:对于任意三位数abc−满足,c>a且a+c=2b,则称这个数为“登高数”.
(1)F(935)=______;F(147)=______;
(2)任意三位数M=abc−,求F(M)的值;
(3)已知S、T均为“登高数”,且2F(S)+3F(T)=24,求S+T的最大值.
22. (本小题8.0分)
已知:射线OP//AE
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO−∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn−1OP的角平分线OBn,其中点B,B1,B2,…,Bn−1,Bn都在射线AE上,试求∠ABnO的度数.
23. (本小题8.0分)
完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE//AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE//AB(已知),
∴∠A=∠CED(______)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(______)
∴DF//AE(______)
∴∠EGF+∠AEG=180°(______)
24. (本小题8.0分)
如图①,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(5,0),(9,0),点D是x轴正半轴上一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.
(Ⅰ)直接写出点C的坐标,并判断△CDE的形状,说明理由;
(Ⅱ)如图②,当点D在线段AB上运动时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长及此时点D的坐标;若不存在,说明理由;
(Ⅲ)当△BDE是直角三角形时,求点D的坐标.(直接写出结果即可)
25. (本小题8.0分)
八(5)班五位同学参加学校举办的“社会主义核心价值观”知识竞赛,试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如表所示
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
答案和解析
1.【答案】A
【解析】解:由题意得,5a+19b=213,
∴a=213−19b5,
∴a+b=213−19b5+b=213−14b5,
∵a+b是关于b的一次函数且a+b随b的增大而减小,
∴当b最小时,a+b取最大值,
又∵a,b是正整数,
∴当b=2时,a+b的最大值=37.
故选:A.
根据题意得出关于a和b的二元一次方程,然后用b表示出a,继而用b表示出a+b,然后可以利用函数的思想得出a+b取得最值的条件,即能得出答案.
本题考查二元一次不定方程的应用,技巧性较强,解答本题的关键是函数思想的应用,同学们要注意掌握这种解题思想,它会在以后的解题中经常用到.
2.【答案】B
【解析】解:设A种糖的单价为x元/千克,则B种糖的单价为(x+40)元/千克,
“什锦糖”甲的单价为12(x+x+40)元/千克,
“什锦糖”乙的单价为2÷(1 x+1x+40)元/千克,
根据题意,得
12(x+x+40)−2÷(1 x+1x+40)=5,
解得x=60,
经检验x=60是分式方程的解,也符合题意,
所以A种糖的单价为60元/千克.
故选:B.
设A种糖的单价为x元/千克,则B种糖的单价为(x+40)元/千克,“什锦糖”甲的单价为12(x+x+40)元/千克,“什锦糖”乙的单价为2÷(1 x+1x+40)元/千克,根据题意列出方程即可求解.
本题考查了二元一次方程组的应用,解决本题的关键是根据题意找到等量关系.
3.【答案】C
【解析】解:∵实数x、y、z满足x2+y2+z2=4,
∴(2x−y)2+(2y−z)2+(2z−x)2=5(x2+y2+z2)−4(xy+yz+xz)=20−2[(x+y+z)2−(x2+y2+z2)]=28−2(x+y+z)2≤28
∴当x+y+z=0时(2x−y)2+(2y−z)2+(2z−x)2的最大值是28.
故选:C.
由题意实数x、y、z满足x2+y2+z2=4,可以将(2x−y)2+(2y−z)2+(2z−x)2,用x2+y2+z2和(xy+yz+xz)表示出来,然后根据完全平方式的基本性质进行求解.
此题主要考查完全平方式的性质及代数式的求值,要学会拼凑多项式.
4.【答案】C
【解析】解:①根据题意得:a@b=(a+b)2−(a−b)2
∴(a+b)2−(a−b)2=0,
整理得:(a+b+a−b)(a+b−a+b)=0,即4ab=0,
解得:a=0或b=0,正确;
②∵a@(b+c)
=(a+b+c)2−(a−b−c)2
=4ab+4ac
a@b+a@c
=(a+b)2−(a−b)2+(a+c)2−(a−c)2
=4ab+4ac,
∴a@(b+c)=a@b+a@c正确;
③a@b=a2+5b2,a@b=(a+b)2−(a−b)2,
令a2+5b2=(a+b)2−(a−b)2,
a2−4ab+5b2=0,即(a−2b)2+b2=0
解得,a=0,b=0,故错误;
④∵a@b=(a+b)2−(a−b)2=4ab,
(a−b)2≥0,则a2−2ab+b2≥0,即a2+b2≥2ab,
∴a2+b2+2ab≥4ab,
∴4ab的最大值是a2+b2+2ab,此时a2+b2+2ab=4ab,
解得,a=b,
∴a@b最大时,a=b,故④正确,
故选C.
根据新定义可以计算出各个小题中的结论是否成立,从而可以得到哪个选项是正确的.
本题考查因式分解的应用、整式的混合运算、完全平方公式,解题的关键是明确题意,找出所求问题需要的条件.
5.【答案】A
【解析】
【分析】
本题考查了因式分解的应用.注意整体思想的运用.
根据乘法分配律可求a,将b变形为2015×2016−(2015−2)×(2016+2),再注意整体思想进行计算,根据提取公因式、完全平方公式和算术平方根可求c,再比较大小即可求解.
【解答】
解:∵a=681×2019−681×2018
=681×(2019−2018)
=681×1
=681,
b=2015×2016−2013×2018
=2015×2016−(2015−2)×(2016+2)
=2015×2016−2015×2016−2×2015+2×2016+2×2
=−4030+4032+4
=6,
c=6782+1358+690+678
=678×(678+1)+679×2+690
=679×(678+2)+690
=680×680−680+690
=680×680+2×680+1−1351
=(680+1)2−1351
=6812−1351,
6<6812−1351<681,
∴b
6.【答案】B
【解析】
【分析】
本题考查了因式分解的方法,掌握因式分解的方法是解决问题的关键.先提出公因式3a,然后用完全平方公式分解因式即可.
【解答】
解:3ax2+24axy+48ay2,
=3a(x2+8xy+16y2),
=3a(x+4y)2.
故选B.
7.【答案】C
【解析】解:①过点E作直线EF//AB,
∵AB//CD,
∴AB//CD//EF,
∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,故本小题错误;
②过点E作直线EF//AB,
∵AB//CD,
∴AB//CD//EF,
∴∠A=∠1,∠2=∠C,
∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C,即∠E=∠A+∠C,故本小题正确;
③过点E作直线EF//AB,
∵AB//CD,
∴AB//CD//EF,
∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC−∠1=180°,即∠A+∠E−∠1=180°,故本选项正确;
④∵∠1+∠CEP=180°,∠CEP+∠C+∠P=180°,∴∠1=∠C+∠P,
∵AB//CD,
∴∠A=∠1,即∠A=∠C+∠P,故本小题正确.
综上所述,正确的小题有②③④共3个.
故选:C.
①过点E作直线EF//AB,由平行线的性质即可得出结论;
②过点E作直线EF//AB,由平行线的性质即可得出结论;
③过点E作直线EF//AB,由平行线的性质可得出∠A+∠E−∠1=180°;
④先得出∠1=∠C+∠P,再根据两直线平行,内错角相等即可作出判断.
本题考查的是平行线的性质,根据题意作出辅助线是解答此题的关键.
8.【答案】C
【解析】
【分析】
本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a//b,b//c⇒a//c.分别过C、D作AB的平行线CM和DN,由平行线的性质可得到∠α+∠β=∠BCD+∠γ,可求得答案
【解答】
解:如图,分别过C、D作AB的平行线CM和DN,
∵AB//EF,
∴AB//CM//DN//EF,
∴∠α=∠BCM,∠MCD=∠NDC,∠NDE=∠γ,
∴∠α+∠β=∠BCM+∠NDC+∠NDE=∠BCM+∠MCD+∠γ,
又BC⊥CD,
∴∠BCD=90°,
又∠BCM+∠MCD=∠BCD,
∴∠BCM+∠MCD=90°,
∴∠α+∠β=90°+∠γ,
即∠α+∠β−∠γ=90°.
故选C.
9.【答案】C
【解析】
【分析】
本题主要考查的知识点是轴对称图形,顺利的找出所有图形的对称轴条数是解题的关键,首先将四个图形的对称轴条数分别找出,再将对称轴条数的和找出即可得到答案.
【解答】
解:∵第一个图形有2条对称轴,第二个图形有8条对称轴,第三个图形没有对称轴,第四个图形没有对称轴,
∴对称轴条数之和为2+8=10(条).
故选C.
10.【答案】D
【解析】解:如图:
∵∠ABC=90°,AB=4,BC=2,
∴AC=AB2+BC2=25,
∵DE//AB,
∴∠EDB=∠DBA,
∵∠EDB=∠BAC,
∴∠DBA=∠BAC,
∵∠ABC=90°,
∴∠CBG=90°−∠DBA=90°−∠BAC=∠ACB,即∠CBF=∠ACB,
∵∠ABC=∠BFC=90°,
∴△BFC∽△CBA,
∴BFBC=BCAC,即BF2=225,
∴BF=255,
故选:D.
由∠ABC=90°,AB=4,BC=2,得AC=25,根据DE//AB,得∠EDB=∠DBA,而∠EDB=∠BAC,即得∠DBA=∠BAC,又∠ABC=90°,可得∠CBF=∠ACB,从而△BFC∽△CBA,即得BF2=225,故BF=255.
本题主要考查直角三角形中的旋转,涉及勾股定理、相似三角形的判定与性质等知识,解题的关键是证明△BFC∽△CBA,利用相似三角形对应边成比例解决问题.
11.【答案】A
【解析】
【分析】
此题主要考查了全面调查和抽样调查,正确把握相关定义是解题关键,直接利用全面调查与抽样调查的意义分析得出答案.
【解答】
解:A.为了了解一本书300页的书稿中错别字的个数,应采用普查的调查方式进行,此选项正确;
B.为了了解我市今年夏季冷饮市场冰激凌的质量可采用抽样的调查方式进行,此选项错误;
C.销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的众数,此选项错误;
D.为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取1000份试卷进行统计分析,在这个问题中,样本是被抽取的1000名学生的成绩,此选项错误;
故选A.
12.【答案】D
【解析】
【分析】
本题考查的是折线统计图,中位数,众数,由折线统计图中所提供的数据,根据中位数,众数的概念分别求得这组数据的中位数,众数即可.
【解答】
解:众数是一组数据中出现次数最多的数,即这组数据的众数是8;
将这组数据从小到大的顺序排列后,第20个和第21个数都是9,所以这组数据的中位数是9.
故选D.
13.【答案】7.5
【解析】解:设紫色、白色、红色三种颜色的兔公仔的成本分别为x元,y元,z元,
根据题意可知,“鸿福兔”礼盒的成本为:(3x+y+z)元,“吉祥兔”礼盒的成本为:(2x+3y+3z)元,
∵每个“鸿福兔”礼盒中所有兔公仔的成本之和为1个紫色兔公仔的5倍,
∴3x+y+z=5x,
∴2x=y+z,
∴2x+3y+3z=2x+3(y+z)=8x,
∵每个“吉祥兔”礼盒的利润率为50%,
∴每个“吉祥兔”礼盒的售价为:8x(1+50%)=12x(元),
∵每个“吉祥兔”礼盒的售价比每个“鸿福兔”礼盒高20%,
∴每个“鸿福兔”礼盒的售价为10x元,
设当天销售“鸿福兔”、“吉祥兔”两种礼盒的数量分别为m个,n个,
∴总销售额为:10xm+12xn=600000①,
∵两种礼盒的总销售额为60万元,总利润率为60%,
∴总成本为:600000÷(1+60%)=375000(元),
∴5xm+8xn=375000②,
联立①②可得4nx=150000,5mx=75000,
∴“鸿福兔”礼盒的总利润是(10x−5x)m=75000=7.5(万元),
故答案为:7.5.
本题考查了三元一次方程组的应用,整体思想的应用,销售问题中各个量之间的关系,解题关键是设出相关未知数,列出方程.
设紫色、白色、红色三种颜色的兔公仔的成本分别为x元,y元,z元,继而表示出“鸿福兔”礼盒的成本,“吉祥兔”礼盒的成本,再根据每个“鸿福兔”礼盒中所有兔公仔的成本之和为1个紫色兔公仔的5倍,用含x的代数式表示出每个“吉祥兔”礼盒的售价,每个“鸿福兔”礼盒的售价,再设当天销售“鸿福兔”、“吉祥兔”两种礼盒的数量分别为m个,n个,结合题意得到4nx=150000,5mx=75000,继而得到“鸿福兔”礼盒的总利润是(10x−5x)m,代入计算即可.
14.【答案】11或−13
【解析】
【分析】
此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
利用完全平方公式的结构特征判断即可求出a的值.
【解答】
解:∵4x2−(a+1)x+9是一个完全平方式,
∴−(a+1)=±2×2×3,
∴−(a+1)=±12
则a=11或−13,
故答案为:11或−13.
15.【答案】5秒或95秒
【解析】
【分析】
本题考查了平行线的判定,读懂题意并熟练掌握平行线的判定方法是解题的关键,要注意分情况讨论.
分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据内错角相等两直线平行,列式计算即可得解;
②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解;
③CD旋转到与AB都在EF的左侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解.
【解答】
解:∵∠EAB=70°,∠DCF=60°,
∴∠BAC=110°,∠ACD=120°,
分三种情况:
如图①,AB与CD在EF的两侧时,
∠ACD=120°−(3t)°,∠BAC=110°−t°,
要使AB//CD,则∠ACD=∠BAC,
即120°−(3t)°=110°−t°,
解得t=5;
②CD旋转到与AB都在EF的右侧时,
∠DCF=360°−(3t)°−60°=300°−(3t)°,∠BAC=110°−t°,
要使AB//CD,则∠DCF=∠BAC,
即300°−(3t)°=110°−t°,
解得t=95;
③CD旋转到与AB都在EF的左侧时,
∠DCF=(3t)°−(180°−60°+180°)=(3t)°−300°,∠BAC=t°−110°,
要使AB//CD,则∠DCF=∠BAC,
即(3t)°−300°=t°−110°,
解得t=95,
∴此情况不存在.
综上所述,当时间t的值为5秒或95秒时,CD与AB平行.
16.【答案】245或5或265
【解析】解:∵1,4,6,9,a的中位数是整数a,
∴a=4或5或6,
当a=4时,这组数据的平均数为15(1+4+6+9+4)=245
当a=5时,这组数据的平均数为15(1+4+6+9+5)=5,
当a=6时,这组数据的平均数为15(1+4+6+9+6)=265,
故答案为:245或5或265.
根据中位数的定义确定整数a的值,由平均数的定义即可得出答案.
本题主要考查了中位数和平均数,解题的关键是根据中位数的定义确定a的值.
17.【答案】解:(1)设一辆A型车装满货物可运货x吨,一辆B型车装满货物可运货y吨,
根据题意,得:2x+y=10x+2y=11,
解得:x=3y=4,
答:一辆A型车装满货物可运货3吨,一辆B型车装满货物可运货4吨;
(2)由题意得:3m+4n=31,
∵m、n均为正整数,
∴m=1n=7或m=5n=4或m=9n=1,
∴该物流公司共有以下三种租车方案,
方案一:租A型车1辆,B型车7辆;
方案二:租A型车5辆,B型车4辆;
方案三:租A型车9辆,B型车1辆.
(3)方案一费用:100×1+120×7=940(元),
方案二费用:100×5+120×4=980(元),
方案三费用:100×9+120×1=1020(元),
∵940<980<1020,
∴方案一:租A型车1辆,B型车7辆,最省钱,最少租车费为940元.
【解析】本题考查了二元一次方程组的应用以及二元一次方程的应用,找准等量关系,正确列出二元一次方程组和二元一次方程是解题的关键.
(1)设一辆A型车装满货物可运货x吨,一辆B型车装满货物可运货y吨,由题意:用两辆A型车和一辆B型车装满货物一次可运货10吨;用一辆A型车和两辆B型车装满货物一次可运货11吨.列出二元一次方程组,解方程组即可;
(2)由题意:某物流公司现有31吨货物,计划同时租用A型车和B型车,一次运完,且恰好每辆车都装满货物.列出二元一次方程,求出正整数解即可.
(3)分别计算三种方案的费用,比较大小即可.
18.【答案】0
【解析】略
19.【答案】解:∵13x2−6xy+y2−4x+1=0,
∴9x2−6xy+y2+4x2−4x+1=0,
即(3x−y)2+(2x−1)2=0,
∴3x−y=0,2x−1=0,
解得x=12,y=32,
当x=12,y=32时,
原式=(12+32)13⋅(12)10=(2×12)10×23=8.
【解析】把13x2分成9x2+4x2,然后分别与剩余的项组成完全平方形式,从而出现两个非负数的和等于0的形式,那么每一个非负数都等于0,从而求出x、y的值,再把x、y的值代入所求式子,计算即可.
本题主要考查完全平方公式、非负数的性质.完全平方公式:(a±b)2=a2±2ab+b2.注意会正确的拆项.
20.【答案】(1)略(2)3
【解析】略
21.【答案】4 6
【解析】解:(1)由题意得:F(935)=|935−539|99=4,F(147)=|147−741|99=6,
故答案为:4,6;
(2)由题意得:M=abc−=100a+10b+c,M′=100c+10b+a,
则F(M)=|100a+10b+c−100c−10b−a|99=|a−c|,
故F (M)=|c−a|;
(3)设S=abc−,T=a′b′c′−,
由(2)知,F(s)=c−a=A,F(T)=c′−a′=B,
由题意得:2A+3B=24,
∵a+c=2b,则c、a同奇或同偶,
故c−a和c′−a′为偶数,
∵2×6+3×4=24,
故A=6,B=4,
要使S+T尽可能大,则a的百位数要尽可能大,
对S而言,c−a=6,
故S最大取369,
对T而言,c′−a′=4,
则T最大可取579,
故S+T的最大值=369+579=948.
(1)根据“倒序数”的定义即可求解;
(2)由题意得:M=abc−=100a+10b+c,M′=100c+10b+a,则F(M)=|100a+10b+c−100c−10b−a|99=|a−c|,进而求解;
(3)由(2)知,F(s)=c−a=A,F(T)=c′−a′,而a+c=2b,则c、a同奇或同偶,求出A=6,B=4,进而求解.
因式分解的应用,主要考查用字母表示数,整式的加减运算、绝对值的意义等,正确理解题意是本题解题的关键.
22.【答案】解:(1)如图1,∵OP//AE,
∴∠A=∠1,
∵∠BOP=58°,OB是∠AOP的角平分线,
∴∠AOP=2∠BOP=116°
∴∠1=180°−116°=64°,
∴∠A=∠1=64°;
(2)如图2,
∵OP//AE,
∴∠POD=∠ADO=39°,
∵OB平分∠AOC,
∴∠AOB=∠BOC,
∵OD平分∠COP,
∴∠COP=2∠DOP=78°,
∴∠ABO−∠AOB=∠COP=78°;
(3)如图3,由(1)可知,∠ABO=12(180°−m),∠AB1O=12(180°−∠OBB1)=12∠ABO=14(180°−m),∠AB2O=18(180°−m),…
则∠ABnO=180°−m2n+1.
【解析】(1)根据平行线的性质得出∠A=∠1,根据平角的定义求得∠AOP=116°,根据角平分线的性质和平行线的性质求得∠A的度数;
(2)利用已知条件和平行线的性质、角平分线的性质解答即可.
(3)根据(1)(2)的规律即可求得.
本题考查了平行线的性质,三角形外角的性质,三角形内角和定理,角平分线的性质,熟练掌握性质定理是解题的关键.
23.【答案】两直线平行,同位角相等 ;
等量代换;
同位角相等,两直线平行;
两直线平行,同旁内角互补 .
【解析】证明:∵DE//AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF//AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
依据两直线平行,同位角相等以及等量代换,即可得到∠A=∠BFD,再根据同位角相等,两直线平行,即可得出DF//AF,进而得出∠EGF+∠AEG=180°.
本题主要考查了平行线的性质与判定,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
24.【答案】解:(Ⅰ)C(7,23),△CDE是等边三角形,
如图1,过点C作CH⊥AB于H,
∵△ABC是等边三角形,CH⊥AB于点H,
∴∠AHC=90°,AH=12AB=12(9−5)=2,
∴OH=OA+AH=7,
∵AC=AB=4,
∴在Rt△ACH中,CH=42−22=23,
∴ C(7,23);
∵△CBE是由△CAD绕点C逆时针旋转60°得到的,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(Ⅱ)存在;
理由如下:如图2,由(Ⅰ)知,△CDE是等边三角形,
∴DE=CD,
由旋转知,BE=AD,
∴C△DBE=BE+DB+DE=AB+DE=4+DE=4+CD,
由垂线段最短可知,CD⊥AB于D时,△BDE的周长最小,此时,由(1)可知CD=23,OD=7,
∴△BDE的周长最小值为4+23,点D(7,0);
(Ⅲ)D(1,0)或(13,0).
【解析】
【分析】
此题是几何变换综合题,主要考查了等边三角形的性质和判定,含30度角的直角三角形,直角三角形的性质,解本题的关键是根据题意作出图形.
(1)如图1,过点C作CH⊥x轴于点H,由△ABC是等边三角形易得AH=12AB=2,结合AC=AB=4、OA=5,可得CH=23,OH=7,由此即可得到点C的坐标;由旋转的性质可知CE=CD,结合旋转角∠DCE=60°可知△CDE是等边三角形;
(2)如图2,由(1)可知△CDE是等边三角形,由此可得DE=CD,由△CDE是由△CAD绕点C旋转得到的,由此可得BE=AD,从而可得△BDE的周长=BD+BE+DE=BD+AD+CD=AB+CD=4+CD,由此可知,当CD⊥AB时,CD最小,此时△BDE的周长最小,由(1)可知,此时CD=23,OD=7,即当点D的坐标为(7,0)时,△BDE的周长最小,最小值为4+23;
(3)如图3,由∠CBE=∠CAD=120°可得∠ABC=60°,由此可得∠DBE=60°≠90°,结合△BDE是直角三角形,可知:存在①∠BED=90°;②∠BDE=90°(如图3,∠BD′E′=90°)两种情况,分两种情况画出符合要求的图形,并结合已知条件进行分析计算即可.
【解答】
解:(Ⅰ)见答案;
(Ⅱ)见答案;
(Ⅲ)如图3,
∵由旋转知,∠CBE=∠CAD=120°,
∵∠ABC=60°,
∴∠DBE=60°≠90°,
∵△BDE是直角三角形,
∴存在∠BED=90°或∠BDE=90°(如图3,∠BD′E′=90°)两种情况,
①当∠BED=90°时,
∵△CDE是等边三角形,
∴∠CED=60°,
∴∠BEC=30°,
∵∠CBE=∠CAD=120°,
∴∠BCE=30°,
∴BE=BC=AB=4,
在Rt△BDE中,∠DBE=∠CBE−∠ABC=60°,
∴BD=2BE=8,
∵OB=9,
∴OD=OB−BD=1,
∴D(1,0);
②当∠BD′E′=90°时,
∵△CD′E′是等边三角形,
∴∠CD′E′=60°,
∴∠BD′C=30°,
∵∠ABC=60°,
∴∠BCD′=30°=∠BD′E,
∴BD′=BC=6,
∵OB=9,
∴OD′=OB+BD′=13,
∴D′(13,0),
即:存在点D使△BDE是直角三角形,此时点D的坐标分别为:(1,0)或(13,0).
25.【答案】解:(1)x−=(19+17+15+17)×5+(2+2+1)×(−2)4=82.5(分),
答:A,B,C,D四位同学成绩的平均分是82.5分.
(2)①设E同学答对x题,答错y题,由题意得
5x−2y=58x+y=13,
解得x=12y=1,
答:E同学答对12题,答错1题.
②C同学,他实际答对14题,答错3题,未答3题.
【解析】(1)直接算出A,B,C,D四位同学成绩的总成绩,再进一步求得平均数即可;
(2)①设E同学答对x题,答错y题,根据对错共20−7=13和总共得分58列出方程组成方程组即可;
②根据表格分别算出每一个人的总成绩,与实际成绩对比:A为19×5=95分正确,B为17×5+2×(−2)=81分正确,C为15×5+2×(−2)=71错误,D为17×5+1×(−2)=83正确,E正确;所以错误的是C,多算7分,也就是答对的少一题,打错的多一题,由此得出答案即可.
此题考查加权平均数的求法,二元一次方程组的实际运用,以及有理数的混合运算等知识,注意理解题意,正确列式解答.
参赛同学
答对题数
答错题数
未答题数
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
湘教版初中数学七年级下册期中测试卷(困难)(含详细答案解析): 这是一份湘教版初中数学七年级下册期中测试卷(困难)(含详细答案解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湘教版初中数学八年级下册期末测试卷(困难)(含答案解析): 这是一份湘教版初中数学八年级下册期末测试卷(困难)(含答案解析),共35页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湘教版初中数学九年级上册期末测试卷(困难)(含答案解析): 这是一份湘教版初中数学九年级上册期末测试卷(困难)(含答案解析),共37页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












