

2022-2023学年重庆市巴南区九年级(上)期末数学试卷
展开2022-2023学年重庆市巴南区九年级(上)期末数学试卷
一、选择题:(本大题共12个小题,每小题4分,共48分.)在每小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请使用2B铅笔将答题卡上对应题目右侧正确答案所在的方框涂黑.
1.(4分)若点A(1,2)在反比例函数y=kx(k≠0)的图象上,则k的值为( )
A.2 B.﹣2 C.3 D.﹣3
2.(4分)下列垃圾分类标识图案,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.(4分)下列事件是必然事件的是( )
A.两个负数的和为正数
B.疫情期间参加聚会不会感染新冠病毒
C.过马路时恰好遇到红灯
D.一个盒子中只装有5个红球,从中摸出一个球是红球
4.(4分)如图,OA是⊙O的半径,点B,C,D是圆上三点,AD=BD,若∠AOD=64°,则∠BCD的度数为( )
A.26° B.30° C.32° D.36°
5.(4分)若a,b是方程x2﹣x﹣2=0的两个根,则a+b的值为( )
A.1 B.﹣1 C.2 D.﹣2
6.(4分)某种药品经过两次降价后,由每盒50元下调至32元,若每次平均降价的百分率是x,则由题意可列方程为( )
A.32(1+x2)=50 B.32(1+x)2=50
C.50(1﹣x2)=32 D.50(1﹣x)2=32
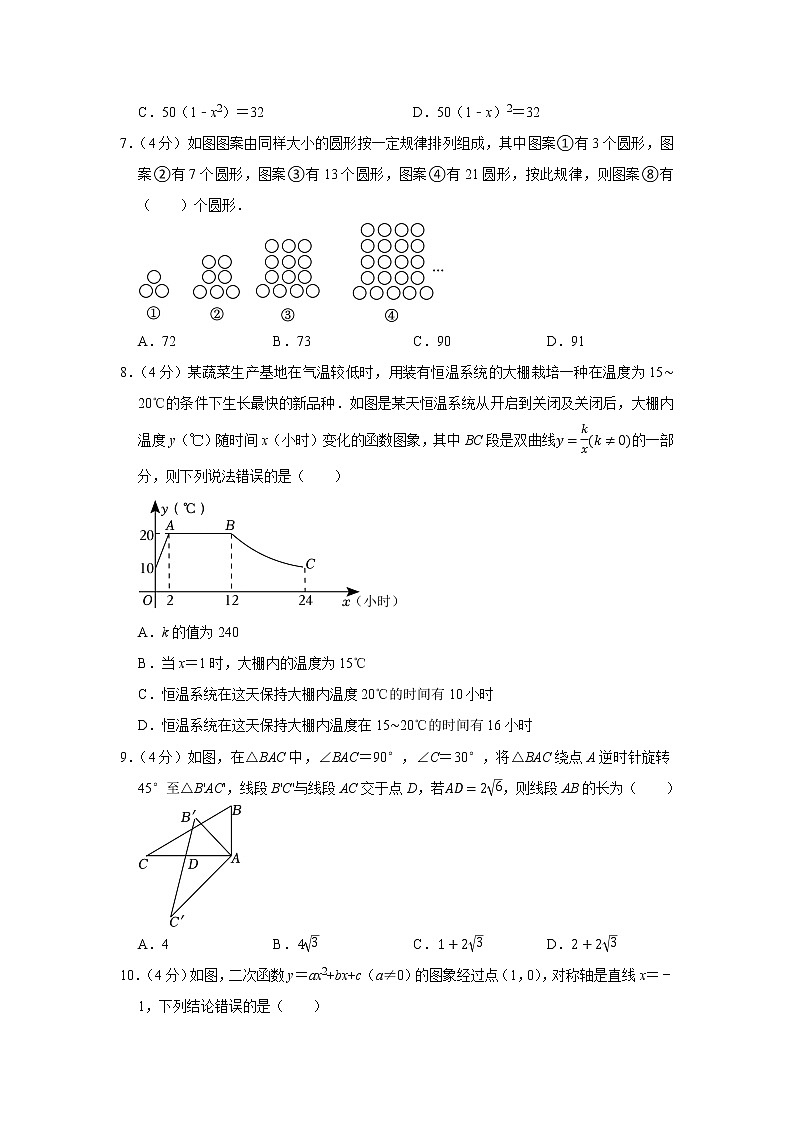
7.(4分)如图图案由同样大小的圆形按一定规律排列组成,其中图案①有3个圆形,图案②有7个圆形,图案③有13个圆形,图案④有21圆形,按此规律,则图案⑧有( )个圆形.
A.72 B.73 C.90 D.91
8.(4分)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为15∼20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=kx(k≠0)的一部分,则下列说法错误的是( )
A.k的值为240
B.当x=1时,大棚内的温度为15℃
C.恒温系统在这天保持大棚内温度20℃的时间有10小时
D.恒温系统在这天保持大棚内温度在15∼20℃的时间有16小时
9.(4分)如图,在△BAC中,∠BAC=90°,∠C=30°,将△BAC绕点A逆时针旋转45°至△B'AC',线段B'C'与线段AC交于点D,若AD=26,则线段AB的长为( )
A.4 B.43 C.1+23 D.2+23
10.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),对称轴是直线x=﹣1,下列结论错误的是( )
A.abc>0 B.2a﹣b=0 C.3a+2c<0 D.9a﹣3b+c=0
11.(4分)如果关于x的分式方程mx−1x−2=2+12−x有整数解,且二次函数y=(m−1)x2+2x+12的图象与x轴有交点,那么符合条件的所有整数m的个数有( )
A.2个 B.3个 C.4个 D.5个
12.(4分)有依次排列的两个整式x﹣y,x+y;第1次操作后得到整式串x﹣y,x+y,2y;第2次操作后得到整式串x﹣y,x+y,2y,y﹣x;其操作规律为:每次操作增加的项为前两项的差(后一项﹣前一项),下列说法:
①第4次操作后的整式串为x﹣y,x+y,2y,y﹣x,﹣x﹣y,﹣2y;
②第101次操作后的整式串各项之和为0;
③第2023次操作后增加的项与第2020次操作后增加的项的和为0.
其中正确的个数是( )
A.3 B.2 C.1 D.0
二、填空题:(本大题共4个小题,每小题4分,共16分.)请将每小题的答案直接填写在答题卡中对应的横线上.
13.(4分)若点A(﹣4,2)与点B(m,n)关于原点对称,则m﹣n= .
14.(4分)在﹣2,﹣1,3,0四个数中,随机选取一个数作为二次函数y=x2+bx+3中b的值,则该二次函数的对称轴在y轴右侧的概率是 .
15.(4分)如图,在扇形AOB中,∠AOB=120°,以点A为圆心,OA为半径画弧交AB于点C.若OA=2,则图中阴影部分的面积为 .
16.(4分)汤圆象征合家团圆美,每年元宵节家家户户都会吃汤圆.为迎接元宵节的到来,某超市12月份购进黑芝麻汤圆、花生汤圆、红糖汤圆三种不同口味的汤圆进行销售.其中每袋黑芝麻汤圆的进价是每袋红糖汤圆的2倍,销售每袋黑芝麻汤圆、花生汤圆、红糖汤圆的利润率分别是20%、30%、20%.该超市12月份销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量之比为3:5:4,销售的总利润率为25%.若1月份三种口味汤圆的进价和售价均保持不变,且1月份该超市销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量之比为5:4:2,则1月份销售的总利润率为 .
三、解答题:(本大题共2个小题,每小题8分,共16分.)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
17.(8分)解下列方程:
(1)(x+2)2=x+2;
(2)3x2+2x﹣3=0.
18.(8分)如图,已知AC为⊙O的直径,B为⊙O上一点.
(1)用尺规作图:过点O作AB的垂线,垂足为D,交劣弧AB于点E;(只保留作图痕迹);
(2)根据(1)中作图,若BC=6,AB=8,求DE的长,请回答下列解答过程中的序号①、②、③、④所对应的内容.
解:∵AC为⊙O的直径,B为⊙O上一点,
∴∠ABC= ;
在Rt△ABC中,BC=6,AB=8,
∴AC=AB2+BC2=10,
∴OE=12AC=5,
∵OE为半径,OE⊥AB,
∴AD= ;
又∵CO=AO,
∴OD是△ABC的中位线,
∴ =12BC=3;
∴DE=OE﹣OD= .
四、解答题:(本大题共7个小题,每小题10分,共70分.)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
19.(10分)如图,在等腰△ABC中,∠BAC=120°,点D为边BC上一点,将线段AD绕点A逆时针旋转120°得到线段AE,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AE∥BC,AE=2,求BC的长.
20.(10分)某校七、八年级学生各有500人,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试.统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:
七年级抽取学生的测试成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
七年级抽取学生的测试成绩统计表
年级
平均数
中位数
众数
优秀率
七年级
8
a
8
80%
八年级
8
8
b
c
(1)直接写出a、b、c的值;
(2)根据所给数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);
(3)现从七、八年级获得10分的4名学生中随机抽取2人参加区党史知识竞赛,请用画树状图或列表的方法求出被选中的2人恰好是七、八年级各1人的概率.
21.(10分)已知一次函数y=2x+4的图象与反比例函数y=kx(k≠0)的图象相交于点A(m,6)和点B(﹣3,n).
(1)求k的值,并在图中画出函数y=kx的图象;
(2)直接写出不等式2x+4>kx的解集;
(3)若点C是点B关于原点的对称点,连接AC、BC,求△ABC的面积.
22.(10分)接种疫苗是阻断新冠病毒传播的有效途径.现有甲、乙两个社区疫苗接种点,已知甲社区接种点平均每天接种疫苗的人数是乙社区接种点平均每天接种疫苗的人数的1.25倍,且甲社区接种点完成3000人的疫苗接种所需的时间比乙社区接种点完成4000人的疫苗接种所需的时间少2天.
(1)求甲、乙两个社区疫苗接种点平均每天接种疫苗的人数;
(2)一段时间后,乙社区疫苗接种点加大了宣传力度.该接种点平均每天接种疫苗的人数比原来平均每天接种疫苗的人数增加了25%,受乙社区疫苗接种点宣传的影响,甲社区疫苗接种点平均每天接种疫苗的人数比原来平均每天接种疫苗的人数减少了5m人,但不低于800人,这样乙社区接种点(m+15)天接种疫苗的人数比甲社区接种点2m天接种疫苗的人数多6000人,求m的值.
23.(10分)对任意的一个正的三位数M,如果其各个数位上的数字均不为零,且满足任意两个数位上的数字之和大于余下数位上的数字,那么称这个三位数M为“三角形数”.把“三角形数”M的任意一个数位上的数字去掉,得到三个两位数,这三个两位数之和记为F(M);把M的百位数字、十位数字、个位数字的和记为G(M).
例如:
146,因为1+4<6,所以146不是“三角形数”;
345,因为3+4>5,3+5>4,4+5>3,所以345是“三角形数”;
所以F(345)=34+35+45=114,G(345)=3+4+5=12.
(1)判断123和298是否为“三角形数”,并说明理由;
(2)已知“三角形数”M满足十位数字比个位数字小3,当20F(M)+22G(M)能被9整除时,求所有满足条件的M的值.
24.(10分)在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于点A、点B(1,0),与y轴交于点C(0,4).
(1)求b,c的值;
(2)如图,设点P为直线AC上方抛物线上的一个动点,过点P作x轴的平行线交AC于点D,过点P作y轴的平行线交x轴于点E,求PD+PE的最大值;
(3)在(2)中PD+PE取得最大值的条件下,将该抛物线向左平移32个单位长度,点F是点P的对应点,平移后的抛物线交y轴于点G,M为平移后的抛物线的对称轴上一点,在平移后的抛物线上确定一点N,使得以点F,G,M,N为顶点的四边形为平行四边形,直接写出所有符合条件的点M的坐标.
25.(10分)如图,在△ABC中,∠BAC=90°,∠C=45°,点D,E分别为边BC,AC上一点,BE与AD相交于点F,将线段AC绕点A顺时针旋转得到线段AG,点G恰好在线段BE的延长线上.
(1)若AG∥BC,AE=2,求CE的长;
(2)若BD=AE,F为BE的中点,猜想线段BE和AD之间存在的数量关系,并证明你的猜想;
(3)在(2)的条件下,将△ABC沿直线BC翻折至△ABC所在平面内得到△PBC,点H在线段PC上,且PH=BD,点M是线段PD上一动点,将△PMH沿直线HM翻折至△PMH所在平面内得到△QMH,点N为线段AB上一动点,当QN+EN取得最小值时,请直接写出AN:MQ的值.
2022-2023学年重庆市巴南区九年级(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共12个小题,每小题4分,共48分.)在每小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请使用2B铅笔将答题卡上对应题目右侧正确答案所在的方框涂黑.
1.(4分)若点A(1,2)在反比例函数y=kx(k≠0)的图象上,则k的值为( )
A.2 B.﹣2 C.3 D.﹣3
【分析】直接把P(1,2)代入反比例函数y=kx(k≠0)中,即可求得.
【解答】解:∵点A(1,2)在反比例函数y=kx(k≠0)的图象上,
∴k=1×2=2,
故选:A.
2.(4分)下列垃圾分类标识图案,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
【解答】解:A、不是中心对称图形,不是轴对称图形,故此选项不合题意;
B、不是中心对称图形,是轴对称图形,故此选项不合题意;
C、既是中心对称图形,也是轴对称图形,故此选项符合题意;
D、不是中心对称图形,不是轴对称图形,故此选项不合题意;
故选:C.
3.(4分)下列事件是必然事件的是( )
A.两个负数的和为正数
B.疫情期间参加聚会不会感染新冠病毒
C.过马路时恰好遇到红灯
D.一个盒子中只装有5个红球,从中摸出一个球是红球
【分析】必然事件就是一定发生的事件,根据定义即可判断.
【解答】解:A、两个负数的和为正数,是不可能事件,故此选项不符合题意;
B、疫情期间参加聚会不会感染新冠病毒,是不可能事件,故此选项不符合题意;
C、过马路时恰好遇到红灯,是随机事件,故此选项不符合题意;
D、一个盒子中只装有5个红球,从中摸出一个球是红球,是必然事件,故此选项符合题意.
故选:D.
4.(4分)如图,OA是⊙O的半径,点B,C,D是圆上三点,AD=BD,若∠AOD=64°,则∠BCD的度数为( )
A.26° B.30° C.32° D.36°
【分析】由AD=BD,根据圆周角定理可得∠AOD=2∠BCD,进而可得答案.
【解答】解:∵AD=BD,
∴∠AOD=2∠BCD,
∴∠BCD=12∠AOD=32°,
故选:C.
5.(4分)若a,b是方程x2﹣x﹣2=0的两个根,则a+b的值为( )
A.1 B.﹣1 C.2 D.﹣2
【分析】根据根与系数的关系可直接得出答案.
【解答】解:∵a,b是方程x2﹣x﹣2=0的两个根,
∴a+b=1.
故选:A.
6.(4分)某种药品经过两次降价后,由每盒50元下调至32元,若每次平均降价的百分率是x,则由题意可列方程为( )
A.32(1+x2)=50 B.32(1+x)2=50
C.50(1﹣x2)=32 D.50(1﹣x)2=32
【分析】关系式为:原价×(1﹣降低的百分率)2=现价.
【解答】解:第一次降低后的价格为:50(1﹣x),
第二次降低后的价格为60(1﹣x)2,
∴可列方程为50(1﹣x)2=32.
故答案为50(1﹣x)2=32,
故选:D.
7.(4分)如图图案由同样大小的圆形按一定规律排列组成,其中图案①有3个圆形,图案②有7个圆形,图案③有13个圆形,图案④有21圆形,按此规律,则图案⑧有( )个圆形.
A.72 B.73 C.90 D.91
【分析】根据已知图形中圆形的个数得出规律,从而得出第⑧个图案的圆形个数.
【解答】解:∵第①个图案有(1+2)个圆形,
第②个图案有(4+3)个圆形,
第③个图案有(9+4)个圆形,
第④个图案有(16+5)个圆形,
......,
∴第n个图案的个数为:(n2+n+1)圆形,
∴第⑧个图案有(82+8+1=73)个圆形,
故选:B.
8.(4分)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为15∼20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=kx(k≠0)的一部分,则下列说法错误的是( )
A.k的值为240
B.当x=1时,大棚内的温度为15℃
C.恒温系统在这天保持大棚内温度20℃的时间有10小时
D.恒温系统在这天保持大棚内温度在15∼20℃的时间有16小时
【分析】根据点B在在在双曲线y=kx上,求出k的值可以判断A;先用待定系数法求出在升温过程中,温度y与时间x的函数解析式,再把x=1代入即可判断B;根据图像即可判断C;把Y=15代入解析式做差即可判断D.
【解答】解:∵点B(12,20)在在双曲线y=kx上,
∴20=k12,
∴k=240,
故A正确;
设在升温过程中,温度y与时间x的函数解析式为y=kx+b,
则2k+b=20b=10,
解得k=5b=10,
∴在升温过程中,温度y与时间x的函数解析式为y=5x+10,
当x=1时,y=15,
故B正确;
根据图象可知,恒温系统在这天保持大棚内温度20℃的时间有12﹣2=10小时,
故C正确;
当y=15时,y=24015=16,
∴恒温系统在这天保持大棚内温度在15∼20℃的时间为16﹣2=14小时,
故D错误.
故选:D.
9.(4分)如图,在△BAC中,∠BAC=90°,∠C=30°,将△BAC绕点A逆时针旋转45°至△B'AC',线段B'C'与线段AC交于点D,若AD=26,则线段AB的长为( )
A.4 B.43 C.1+23 D.2+23
【分析】作DH⊥AB'于H,利用旋转的性质得∠CAB'=∠BAB'=45°,∠B=∠B',再解△ADB'即可.
【解答】解:作DH⊥AB'于H,
∵将△BAC绕点A逆时针旋转45°至△B'AC',
∴∠CAB'=∠BAB'=45°,∠B=∠B',
∵AD=26,
∴DH=AH=23,
∵∠BAC=90°,∠C=30°,
∴∠B=∠B'=60°,
∴B'H=2,
∴AB'=AH+B'H=23+2,
故选:D.
10.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),对称轴是直线x=﹣1,下列结论错误的是( )
A.abc>0 B.2a﹣b=0 C.3a+2c<0 D.9a﹣3b+c=0
【分析】由图可知开口向下,即a<0,图象交于y轴正半轴,可得c>0,对称轴x=−b2a=−1,可得b<0和2a﹣b=0,可判断A选项和C选项;
由图可得当x=1时,y=a+b+c=0,由2a﹣b=0可得b=2a,即a+2a+c=0,可得3a+2c>0,即可判断C选项;
由抛物线的对称性可知点(﹣3,0)在二次函数y=ax2+bx+c(a≠0)的图象上,可得9a﹣3b+c=0,即可判断D选项.
【解答】解:∵二次函数开口向下,
∴a<0,
∵图象交于y轴正半轴,
∴c>0,
∵对称轴x=−b2a=−1,
∴b<0,
∴abc>0,
故A选项正确,不符合题意;
∵对称轴x=−b2a=−1,
∴﹣b=﹣2a,
∴2a﹣b=0,
故B选项正确,不符合题意;
∵2a﹣b=0,
∴b=2a,
∵当x=1时,y=a+b+c=0,
即a+2a+c=0,
∴3a+c=0,
∵c>0,
∴3a+2c>0,
故C选项错误,符合题意;
∵二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),对称轴是直线x=﹣1,
∴(﹣3,0)在二次函数y=ax2+bx+c(a≠0)的图象上,
∴9a﹣3b+c=0,
故D选项正确,不符合题意;
故选:C.
11.(4分)如果关于x的分式方程mx−1x−2=2+12−x有整数解,且二次函数y=(m−1)x2+2x+12的图象与x轴有交点,那么符合条件的所有整数m的个数有( )
A.2个 B.3个 C.4个 D.5个
【分析】先利用二次函数y=(m−1)x2+2x+12的图象与x轴无交点得到m的取值范围,解分式方程,结合m的取值范围与题意求出所有符合条件的m值.
【解答】解:∵二次函数y=(m−1)x2+2x+12的图象与x轴无交点,
∴22﹣4(m﹣1)×12<0,
解得:m>3,
分式方程mx−1x−2=2+12−x的解为x=42−m,
∵关于x的分式方程mx−1x−2=2+12−x有整数解,
∴m=4或6,
故选:A.
12.(4分)有依次排列的两个整式x﹣y,x+y;第1次操作后得到整式串x﹣y,x+y,2y;第2次操作后得到整式串x﹣y,x+y,2y,y﹣x;其操作规律为:每次操作增加的项为前两项的差(后一项﹣前一项),下列说法:
①第4次操作后的整式串为x﹣y,x+y,2y,y﹣x,﹣x﹣y,﹣2y;
②第101次操作后的整式串各项之和为0;
③第2023次操作后增加的项与第2020次操作后增加的项的和为0.
其中正确的个数是( )
A.3 B.2 C.1 D.0
【分析】根据题意,可以写出第4次操作后的整式串,从而可以判断①;然后再写出第5次和第6次操作的整式串,从而可以发现变化特点,从而可以判断②③.
【解答】解:由题意可得,
第4次操作后的整式串为x﹣y,x+y,2y,y﹣x,﹣x﹣y,﹣2y,故①正确,符合题意;
第4次操作后的整式串为x﹣y,x+y,2y,y﹣x,﹣x﹣y,﹣2y,这些整式的和为0,
第5次操作后的整式串为x﹣y,x+y,2y,y﹣x,﹣x﹣y,﹣2y,x﹣y,
第6次操作后的整式串为x﹣y,x+y,2y,y﹣x,﹣x﹣y,﹣2y,x﹣y,x+y,
则第5次的最后一项和第一次的的第一次的第一项一眼,故从第5次开始,每6次一个循环,
∵(101﹣4)÷6=97÷6=16……1,
则第101次操作后的整式串各项之和为x﹣y,故②错误,不符合题意;
∵(2020﹣4)÷6=336,(2023﹣4)÷6=336……3,
∴第2020次操作后增加的项为﹣2y,第2023次操作后增加的项为2y,
∴第2023次操作后增加的项与第2020次操作后增加的项的和为:2y+(﹣2y)=0,故③正确,符合题意;
故选:B.
二、填空题:(本大题共4个小题,每小题4分,共16分.)请将每小题的答案直接填写在答题卡中对应的横线上.
13.(4分)若点A(﹣4,2)与点B(m,n)关于原点对称,则m﹣n= 6 .
【分析】直接利用关于原点对称点的性质得出m,n的值,进而得出答案.
【解答】解:∵点A(﹣4,2)与点B(m,n)关于原点对称,
∴m=4,n=﹣2,
∴m﹣n=4﹣(﹣2)=6.
故答案为:6.
14.(4分)在﹣2,﹣1,3,0四个数中,随机选取一个数作为二次函数y=x2+bx+3中b的值,则该二次函数的对称轴在y轴右侧的概率是 12 .
【分析】二次函数的对称轴在y轴的右侧得出a<0,从所列4个数中找到a<0的个数,再根据概率公式求解可得.
【解答】解:∵从﹣2,﹣1,3,0四个数中随机选取一个数,共有4种等可能结果,其中使该二次函数的对称轴在y轴的右侧的有﹣1、﹣2这2种结果,
∴该二次函数的对称轴在y轴的右侧的概率为24=12.
故答案为:12.
15.(4分)如图,在扇形AOB中,∠AOB=120°,以点A为圆心,OA为半径画弧交AB于点C.若OA=2,则图中阴影部分的面积为 3 .
【分析】阴影的面积=扇形OBC的面积+△AOC的面积﹣扇形AOC的面积,由扇形面积公式,三角形面积公式,即可解决问题.
【解答】解:连接OC,AC,
由题意得:△AOC是等边三角形,
∴∠AOC=∠CAO=60°,∠BOC=120°﹣60°=60°,AO=OC=2,
∴扇形OBC的面积=扇形AOC的面积=60×π×22360=2π3,△AOC的面积=34AO2=34×22=3,
∴阴影的面积=扇形OBC的面积+△AOC的面积﹣扇形AOC的面积=2π3+3−2π3=3.
故答案为:3.
16.(4分)汤圆象征合家团圆美,每年元宵节家家户户都会吃汤圆.为迎接元宵节的到来,某超市12月份购进黑芝麻汤圆、花生汤圆、红糖汤圆三种不同口味的汤圆进行销售.其中每袋黑芝麻汤圆的进价是每袋红糖汤圆的2倍,销售每袋黑芝麻汤圆、花生汤圆、红糖汤圆的利润率分别是20%、30%、20%.该超市12月份销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量之比为3:5:4,销售的总利润率为25%.若1月份三种口味汤圆的进价和售价均保持不变,且1月份该超市销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量之比为5:4:2,则1月份销售的总利润率为 24% .
【分析】根据题意设出每种汤圆每袋的进价,即可得出销售销售每袋黑芝麻汤圆、花生汤圆、红糖汤圆的利润分别为0.4x元、0.3y元、0.2x元,然后根据题意设出12月份销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量分别为3a、5a、4a袋,根据题意列出∴1.2ax+1.5ay+0.8ax6ax+5ay+4ax×100%=25%,得出y与x的关系,然后在设出1月份该超市销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量分别为5b、4b、2b袋,即可得出1月份销售的总利润率=2bx+1.2by+0.4bx10bx+4by+2bx×100%=24%.
【解答】解:设每袋红糖汤圆的进价为x元,每袋花生汤圆的进价为y元,则每袋黑芝麻汤圆的进价为2x元,
∵销售每袋黑芝麻汤圆、花生汤圆、红糖汤圆的利润率分别是20%、30%、20%,
∴销售每袋黑芝麻汤圆、花生汤圆、红糖汤圆的利润分别为0.4x元、0.3y元、0.2x元,
设12月份销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量分别为3a、5a、4a袋,
∵12月份销售的总利润率为25%,
∴1.2ax+1.5ay+0.8ax6ax+5ay+4ax×100%=25%,整理得:2x+1.5y10x+5y=14,
解得:y=2x,
根据题意可设1月份该超市销售黑芝麻汤圆、花生汤圆、红糖汤圆三种汤圆的数量分别为5b、4b、2b袋,
则1月份销售的总利润率=2bx+1.2by+0.4bx10bx+4by+2bx×100%=4.8x20x×100%=24%;
故答案为:24%.
三、解答题:(本大题共2个小题,每小题8分,共16分.)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
17.(8分)解下列方程:
(1)(x+2)2=x+2;
(2)3x2+2x﹣3=0.
【分析】(1)利用因式分解法求解即可;
(2)利用公式法求解即可.
【解答】解:(1)(x+2)2=x+2,
(x+2)2﹣(x+2)=0,
(x+2)(x+1)=0,
∵x+2=0或x+1=0,
∴x1=﹣2,x2=﹣1;
(2)3x2+2x﹣3=0,
∵a=3,b=2,c=﹣3,
∴Δ=22﹣4×3×(﹣3)=40>0,
∴x=−2±402×3=−1±103,
∴x1=−1+103,x2=−1−103.
18.(8分)如图,已知AC为⊙O的直径,B为⊙O上一点.
(1)用尺规作图:过点O作AB的垂线,垂足为D,交劣弧AB于点E;(只保留作图痕迹);
(2)根据(1)中作图,若BC=6,AB=8,求DE的长,请回答下列解答过程中的序号①、②、③、④所对应的内容.
解:∵AC为⊙O的直径,B为⊙O上一点,
∴∠ABC= 90° ;
在Rt△ABC中,BC=6,AB=8,
∴AC=AB2+BC2=10,
∴OE=12AC=5,
∵OE为半径,OE⊥AB,
∴AD= BD(或12AB) ;
又∵CO=AO,
∴OD是△ABC的中位线,
∴ OD =12BC=3;
∴DE=OE﹣OD= 2 .
【分析】(1)根据作图过程即可完成作图;
(2)结合(1)根据三角形中位线定理即可完成填空.
【解答】解:(1)如图所示,即为所求;
(2)∵AC为⊙O的直径,B为⊙O上一点,
∴∠ABC=90°;
在Rt△ABC中,BC=6,AB=8,
∴AC==AB2+BC2=10,
∴OE=12AC=5,
∵OE为半径,OE⊥AB,
∴AD=BD(或12AB);
又∵CO=AO,
∴OD是△ABC的中位线,
∴OD=12BC=3;
∴DE=OE﹣OD=2.
故答案为:90°,BD(或12AB),OD,2.
四、解答题:(本大题共7个小题,每小题10分,共70分.)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
19.(10分)如图,在等腰△ABC中,∠BAC=120°,点D为边BC上一点,将线段AD绕点A逆时针旋转120°得到线段AE,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AE∥BC,AE=2,求BC的长.
【分析】(1)根据旋转的性质得∠BAC=∠DAE,可得∠BAD=∠CAE,再利用SAS即可证明△ABD≅△ACE;
(2)根据平行线的性质和等腰三角形的判定可得AD=BD=2,再利用含30°角的直角三角形的性质求出CD的长,进而解决问题.
【解答】(1)证明:由旋转,得AD=AE,∠DAE=120°,
∵∠BAC=120°,
∴∠BAC=∠DAE,
∴∠BAD+∠DAC=∠DAC+∠CAE,
即∠BAD=∠CAE,
∵△ABC为等腰三角形,
∴AB=AC,
在△ABD和△ACE中,
AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≅△ACE(SAS);
(2)解:∵AB=AC,∠BAC=120°,
∴∠B=∠ACB=30°,
∵AE∥BC,
∴∠EAC=∠ACB=30°,
∴∠BAD=∠EAC=30°,
∴∠B=∠BAD,
∴BD=AD,
∵∠DAE=120°,∠EAC=30°,
∴∠CAD=90°,
在Rt△ACD中,
∵∠ACD=30°,DC=2AD,
∵AE=AD=2,
∴BC=BD+DC=3AD=6.
20.(10分)某校七、八年级学生各有500人,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试.统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:
七年级抽取学生的测试成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
七年级抽取学生的测试成绩统计表
年级
平均数
中位数
众数
优秀率
七年级
8
a
8
80%
八年级
8
8
b
c
(1)直接写出a、b、c的值;
(2)根据所给数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);
(3)现从七、八年级获得10分的4名学生中随机抽取2人参加区党史知识竞赛,请用画树状图或列表的方法求出被选中的2人恰好是七、八年级各1人的概率.
【分析】(1)由众数和中位数的定义求解即可;
(2)七、八年级的平均数和中位数相同,七年级的众数大于八年级的优秀率,即可求解;
(3)画树状图,共有12种等可能的结果,被选中的2人恰好是七、八年级各1人的结果有6种,再由概率公式求解即可.
【解答】解:(1)a=8,b=7,c=60%;
(2)七年级的学生党史知识掌握得较好.
理由:七年级、八年级学生的平均测试成绩均为(8分),且七年级学生的测试成绩的众数(8分)高于八年级学生的测试成绩的众数(7分).
(3)把七年获得(10分)的学生记为A,八年级获得(10分)的学生记为B,画树状图如下:
共有12种等可能的结果,其中被选中的2人恰好是七、八年级各1人的结果有6种,
所以,P(被选中的2人恰好是七、八年级各1人)=612=12.
21.(10分)已知一次函数y=2x+4的图象与反比例函数y=kx(k≠0)的图象相交于点A(m,6)和点B(﹣3,n).
(1)求k的值,并在图中画出函数y=kx的图象;
(2)直接写出不等式2x+4>kx的解集;
(3)若点C是点B关于原点的对称点,连接AC、BC,求△ABC的面积.
【分析】(1)根据一次函数解析式求出A点和B点的坐标,然后用待定系数法求出反比例函数的表达式即可;
(2)根据图象直接得出不等式的解集即可;
(3)根据对称求出C点坐标,根据A点、B点和C点坐标确定三角形的底和高,进而求出三角形的面积即可.
【解答】解:(1)将点A(m,6)代入一次函数y=2x+4得,
∴m=1,
∴点A的坐标为(1,6),
把点A(1,6)代入反比例函数y=kx得,解得k=6,
∴反比例函数的解析式为y=6x;
∴反比例函数y=6x的图象如图;
(2)不等式2x+4>kx的解集为:﹣3<x<0或x>1;
(3)将点B(﹣3,n)代入反比例函数y=6x得,n=﹣2;
∵点C是点B关于原点的对称点,
∴点C的坐标为(3,2),
∴△ABC的面积=6×8−12×8×4−12×2×4−12×4×6=16.
22.(10分)接种疫苗是阻断新冠病毒传播的有效途径.现有甲、乙两个社区疫苗接种点,已知甲社区接种点平均每天接种疫苗的人数是乙社区接种点平均每天接种疫苗的人数的1.25倍,且甲社区接种点完成3000人的疫苗接种所需的时间比乙社区接种点完成4000人的疫苗接种所需的时间少2天.
(1)求甲、乙两个社区疫苗接种点平均每天接种疫苗的人数;
(2)一段时间后,乙社区疫苗接种点加大了宣传力度.该接种点平均每天接种疫苗的人数比原来平均每天接种疫苗的人数增加了25%,受乙社区疫苗接种点宣传的影响,甲社区疫苗接种点平均每天接种疫苗的人数比原来平均每天接种疫苗的人数减少了5m人,但不低于800人,这样乙社区接种点(m+15)天接种疫苗的人数比甲社区接种点2m天接种疫苗的人数多6000人,求m的值.
【分析】(1)设乙社区疫苗接种点平均每天接种x人,则甲社区疫苗接种点平均每天接种1.25x人,根据题意:甲社区接种点完成3000人的疫苗接种所需的时间比乙社区接种点完成4000人的疫苗接种所需的时间少2天.即可列出关于x的分式方程,解分式方程即可;
(2)根据题意:乙社区接种点(m+15)天接种疫苗的人数比甲社区接种点2m天接种疫苗的人数多6000人,列出关于m的一元二次方程,解方程,即可解决问题.
【解答】解:(1)设乙社区疫苗接种点平均每天接种x人,则甲社区疫苗接种点平均每天接种1.25x人,
由题意得:30001.25x=4000x−2,
解得:x=800,
经检验,x=800是原分式方程的解,且符合题意,
∴1.25x=1.25×800=1000,
答:甲社区疫苗接种点平均每天接种1000人,乙社区疫苗接种点平均每天接种800人;
(2)由题意得:(1000﹣5m)×2m+6000=800×(1+25%)×(m+15),
整理得:m2﹣100m+900=0,
解得:m1=90,m2=10,
∵1000﹣5m≥800,
∴m≤40,
∴m1=90不符合题意舍去,
答:m的值为10.
23.(10分)对任意的一个正的三位数M,如果其各个数位上的数字均不为零,且满足任意两个数位上的数字之和大于余下数位上的数字,那么称这个三位数M为“三角形数”.把“三角形数”M的任意一个数位上的数字去掉,得到三个两位数,这三个两位数之和记为F(M);把M的百位数字、十位数字、个位数字的和记为G(M).
例如:
146,因为1+4<6,所以146不是“三角形数”;
345,因为3+4>5,3+5>4,4+5>3,所以345是“三角形数”;
所以F(345)=34+35+45=114,G(345)=3+4+5=12.
(1)判断123和298是否为“三角形数”,并说明理由;
(2)已知“三角形数”M满足十位数字比个位数字小3,当20F(M)+22G(M)能被9整除时,求所有满足条件的M的值.
【分析】(1)根据“三角形数”的概念求解即可;
(2)设“三角形数”M的百位上的数字为a,十位上的数字为b,个位上的数字为c,知M=abc,且c=b+3,根据题意得F(M)=ab+ac+bc=20a+11b+2c,G(M)=a+b+c,继而得20F(M)+22G(M)=20(20a+11b+2c)+22(a+b+c)=47×9a+27×9b+7×9c﹣(a+b+c),根据20F(M)+22G(M)能被9整除,知a+b+c能被9整除,结合c=b+3知a+b+c=a+2b+3;由1≤a≤9,1≤b≤6,1≤c≤9,且a,b,c为整数得a+2b+3=9或18,再分别讨论求解即可.
【解答】解:(1)∵1+2=3,
∴123不是“三角形数”;
∵2+9>8,8+9>2,2+8>9,
∴298是“三角形数”.
(2)设“三角形数”M的百位上的数字为a,十位上的数字为b,个位上的数字为c,
则M=abc,且c=b+3,
根据题意得,F(M)=ab+ac+bc=20a+11b+2c,G(M)=a+b+c,
∴20F(M)+22G(M)
=20(20a+11b+2c)+22(a+b+c)
=47×9a+27×9b+7×9c﹣(a+b+c),
∵20F(M)+22G(M)能被9整除,
∴a+b+c能被9整除,
∵c=b+3,
∴a+b+c=a+2b+3;
∵1≤a≤9,1≤b≤6,1≤c≤9,且a,b,c为整数,
∴a+2b+3=9或18,
当a+2b+3=9时,
∴a=2,b=2,c=5;a=4,b=1,c=4;
当a+2b+3=18时,
∴a=3,b=6,c=9;a=5,b=5,c=8;a=7,b=4,c=7;a=9,b=3,c=6;
∴M=225,414,369,558,747,936;
∵其中225,369,936不是“三角形数”,
∴满足条件的M的值为414,558,747.
24.(10分)在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于点A、点B(1,0),与y轴交于点C(0,4).
(1)求b,c的值;
(2)如图,设点P为直线AC上方抛物线上的一个动点,过点P作x轴的平行线交AC于点D,过点P作y轴的平行线交x轴于点E,求PD+PE的最大值;
(3)在(2)中PD+PE取得最大值的条件下,将该抛物线向左平移32个单位长度,点F是点P的对应点,平移后的抛物线交y轴于点G,M为平移后的抛物线的对称轴上一点,在平移后的抛物线上确定一点N,使得以点F,G,M,N为顶点的四边形为平行四边形,直接写出所有符合条件的点M的坐标.
【分析】(1)用待定系数法可得b的值为﹣3,c的值为4;
(2)由y=﹣x2﹣3x+4,可得点A(﹣4,0),从而可得直线AC的解析式为y=x+4,设点P(m,﹣m2﹣3m+4),则PD+PE=﹣m2﹣4m+(﹣m2﹣3m+4)=﹣2m2﹣7m+4=﹣2(m+74)2+818,由二次函数性质可得答案;
(3)由(2)得P(−74,9916),将抛物线y=﹣x2﹣3x+4向左平移32个单位长度得y=﹣(x+32)2﹣3(x+32)+4=﹣x2﹣6x−114=−(x+3)2+254,可得F(−134,9916),G(0,−114),设M(﹣3,n),N(t,﹣t2﹣6t−114),分三种情况:①若FG,MN为对角线,则FG的中点与MN的中点重合,−134=−3+t9916−114=n−t2−6t−114,②若FM,GN为对角线,则FM的中点与GN的中点重合,−134−3=t9916+n=−t2−6t−114−114,③若FN,GM为对角线,则FN的中点与GM的中点重合,−134+t=−39916−t2−6t−114=n−114,解方程组即得答案.
【解答】解:(1)把点B(1,0),C(0,4)代入抛物线y=﹣x2+bx+c得,
−1+b+c=0c=4,
解得b=−3c=4,
∴b的值为﹣3,c的值为4;
(2)由(1)知y=﹣x2﹣3x+4,
把y=0代入y=﹣x2﹣3x+4,得﹣x2﹣3x+4=0,
解得x1=﹣4,x2=1,
∴点A(﹣4,0),
设直线AC的解析式为y=px+q,把A(﹣4,0),C(0,4)代入得,
∴−4p+q=0q=4,
解得p=1q=4,
∴直线AC的解析式为y=x+4,
设点P(m,﹣m2﹣3m+4),则PE=﹣m2﹣3m+4,
在y=x+4中,令y=﹣m2﹣3m+4,得x=﹣m2﹣3m;
∴D(﹣m2﹣3m,﹣m2﹣3m+4),
∴PD=﹣m2﹣3m﹣m=﹣m2﹣4m;
∴PD+PE=﹣m2﹣4m+(﹣m2﹣3m+4)=﹣2m2﹣7m+4=﹣2(m+74)2+818,
∵﹣2<0,
∴当m=−74时,PD+PE有最大值818;
(3)由(2)知,PD+PE取得最大值时,P(−74,9916),
将抛物线y=﹣x2﹣3x+4向左平移32个单位长度得y=﹣(x+32)2﹣3(x+32)+4=﹣x2﹣6x−114=−(x+3)2+254,
∴F(−134,9916),G(0,−114),平移后抛物线对称轴是直线x=﹣3,
设M(﹣3,n),N(t,﹣t2﹣6t−114),
①若FG,MN为对角线,则FG的中点与MN的中点重合,
∴−134=−3+t9916−114=n−t2−6t−114,
解得t=−14n=194;
∴M(﹣3,194);
②若FM,GN为对角线,则FM的中点与GN的中点重合,
∴−134−3=t9916+n=−t2−6t−114−114,
解得t=−254n=−534,
∴M(﹣3,−534);
③若FN,GM为对角线,则FN的中点与GM的中点重合,
−134+t=−39916−t2−6t−114=n−114,
解得t=14n=378,
∴M(﹣3,378),
综上所述,点M的坐标分别为:(−3,378)或(−3,−534)或(−3,194).
25.(10分)如图,在△ABC中,∠BAC=90°,∠C=45°,点D,E分别为边BC,AC上一点,BE与AD相交于点F,将线段AC绕点A顺时针旋转得到线段AG,点G恰好在线段BE的延长线上.
(1)若AG∥BC,AE=2,求CE的长;
(2)若BD=AE,F为BE的中点,猜想线段BE和AD之间存在的数量关系,并证明你的猜想;
(3)在(2)的条件下,将△ABC沿直线BC翻折至△ABC所在平面内得到△PBC,点H在线段PC上,且PH=BD,点M是线段PD上一动点,将△PMH沿直线HM翻折至△PMH所在平面内得到△QMH,点N为线段AB上一动点,当QN+EN取得最小值时,请直接写出AN:MQ的值.
【分析】(1)可证明△AGE∽△CBE,从而CEAE=BCAG,进一步得出结果;
(2)作BT∥AC,交AD的延长线于T,作AR⊥BC于R,△AEF≌△TBF,进而得出BD=BT,进而推出∠ADC=∠BDT,可证明∠AEB=∠FAE,从而∠AEB=∠ADC,进而证明△ARD∽△BAE,进一步得出结论;
(3)可推出点Q在以H为圆心,2−1为半径的圆上运动,作点E关于AB的对称点R,连接RH交⊙H于点Q,则QN+EN最小,设AC=1,可推出MQ=PM=PH=BD=2−1,AN=(2−1)2,进而得出结果.
【解答】解:(1)∵∠BAC=90°,∠C=45°,∠C=∠ABC=45°,
∴AB=AC,BC=2AC,
∵线段AC绕点A顺时针旋转得到线段AG,
∴AG=AC,
∴BC=2AG,
∵AG∥BC,
∴∠G=∠CBE,∠C=∠GAE,
∴△AGE∽△CBE,
∴CEAE=BCAG,
∴CE2=2,
∴CE=22;
(2)如图1,
结论:BE=2AD,理由如下:
作BT∥AC,交AD的延长线于T,作AR⊥BC于R,
∴∠T=∠EAF,∠TBF=∠AEF,∠ARD=90°,
∵点F是BE的中点,
∴EF=BF,
∴△AEF≌△TBF(AAS),
∴BT=AE,
∵BD=AE,
∴BT=BD,
∴∠T=∠BDT,
∵∠ADC=∠BDT,
∴∠ADC=∠FAE,
在Rt△ABE中,点F是BE的中点,
∴AF=EF,
∴∠AEB=∠FAE,
∴∠AEB=∠ADC,
∵∠ARD=∠BAE=90°,
∴△ARD∽△BAE,
∴BEAD=ABAR=2,
∴BE=2AD;
(3)如图2,
可得四边形ABPC是正方形,
设CD=AB=AC=PC=1,则BC=2,BD=AE=PH=HQ=2−1,CH=2−2,
∴点Q在以H为圆心,2−1为半径的圆上运动,作点E关于AB的对称点R,连接RH交⊙H于点Q,
则QN+EN最小,
∵AR=AE=2−1,
∴CR=AR+AC=2,
∴tanR=CHCR=2−22=2−1,
由(1)中知:AB=AG,
∴∠G=∠ABE,
∵AG∥BC,
∴∠G=∠CBE,
∴∠ABE=∠CBE=12∠ABC=22.5°,
∴tan22.5°=AEAB=2−1,
∴∠R=22.5°,
∴∠CHR=90°﹣∠R=67.5°,
∵CD=PC,∠PCB=45°,
∴∠CPD=∠CDP=67.5°,
∴RH∥PD,
∴∠MHQ=∠PMH,
∵∠PHM=∠QHM,
∴∠PHM=∠PMH,
∴MQ=PM=PH=BD=2−1,
∵tanR=ANAR,
∴tan15°=AN2−1=2−1,
∴AN=(2−1)2,
∴AN:MQ的值为2−1.
重庆市巴南区2022-2023学年七年级(上)期末数学试卷(含答案 人教版): 这是一份重庆市巴南区2022-2023学年七年级(上)期末数学试卷(含答案 人教版),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年重庆市巴南区科学城中学九年级(上)开学数学试卷(含解析): 这是一份2023-2024学年重庆市巴南区科学城中学九年级(上)开学数学试卷(含解析),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年重庆市巴南区八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年重庆市巴南区八年级(下)期末数学试卷(含解析),共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












