高中数学湘教版（2019）必修 第一册4.4 函数与方程公开课ppt课件

这是一份高中数学湘教版（2019）必修 第一册4.4 函数与方程公开课ppt课件，共24页。PPT课件主要包含了函数的零点，即时巩固，求函数的零点，反思感悟等内容，欢迎下载使用。

1.根据二次函数零点了解一般函数的零点,并会求简单函数的零点.2.了解函数的零点与方程解的关系.3.结合具体连续函数及其图象的特点,了解函数求零点的方法（零点存在定理）.核心素养：数学抽象，逻辑推理
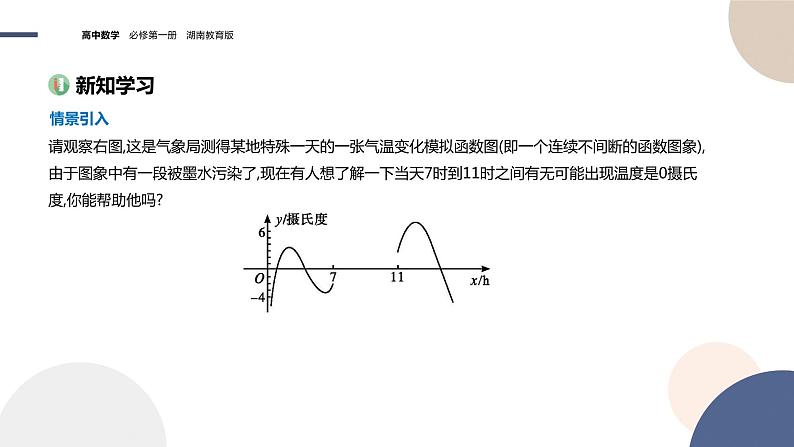
请观察右图,这是气象局测得某地特殊一天的一张气温变化模拟函数图(即一个连续不间断的函数图象),由于图象中有一段被墨水污染了,现在有人想了解一下当天7时到11时之间有无可能出现温度是0摄氏度,你能帮助他吗?
二、函数零点的判断方法（零点存在定理）
跟踪训练　已知函数f(x)=x2+3(m+1)x+n的零点是1和2,求函数y=lgn(mx+1)的零点.
二、函数零点个数的判断
三、已知零点个数求参数的取值范围
答案 (1,+∞)
四、二次函数的零点综合问题
1.如下图四个函数图象,在区间(-∞,0)内存在零点的函数是(　　)
4.已知函数y=ax2-x-1只有一个零点,则实数a的值为　　　　　.