(新高考)高考数学一轮基础复习讲义11.1随机事件的概率(2份打包，教师版+原卷版)

判断下列结论是否正确(请在括号中打“√”或“×”)

(1)事件发生频率与概率是相同的．(　 　)

(2)随机事件和随机试验是一回事．(　 　)

(3)在大量重复试验中，概率是频率的稳定值．(　 　)

(4)两个事件的和事件是指两个事件都得发生．(　 　)

(5)对立事件一定是互斥事件，互斥事件不一定是对立事件．(　 　)

(6)两互斥事件的概率和为1. (  　)

无

题型一　事件关系的判断

例1　(1)从1,2,3，…，7这7个数中任取两个数，其中：

①恰有一个是偶数和恰有一个是奇数；

②至少有一个是奇数和两个都是奇数；

③至少有一个是奇数和两个都是偶数；

④至少有一个是奇数和至少有一个是偶数．

上述事件中，是对立事件的是(　　)

A．①  B．②④  C．③  D．①③

(2)设条件甲：“事件A与事件B是对立事件”，结论乙：“概率满足P(A)＋P(B)＝1”，则甲是乙的(　　)

A．充分不必要条件   B．必要不充分条件

C．充要条件   D．既不充分也不必要条件

(3)在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是，那么概率是的事件是(　　)

A．至多有一张移动卡   B．恰有一张移动卡

C．都不是移动卡   D．至少有一张移动卡

　从装有两个白球和两个黄球的口袋中任取2个球，以下给出了四组事件：

①至少有1个白球与至少有1个黄球；

②至少有1个黄球与都是黄球；

③恰有1个白球与恰有1个黄球；

④恰有1个白球与都是黄球．

其中互斥而不对立的事件共有(　　)

A．0组  B．1组  C．2组  D．3组

题型二　随机事件的频率与概率

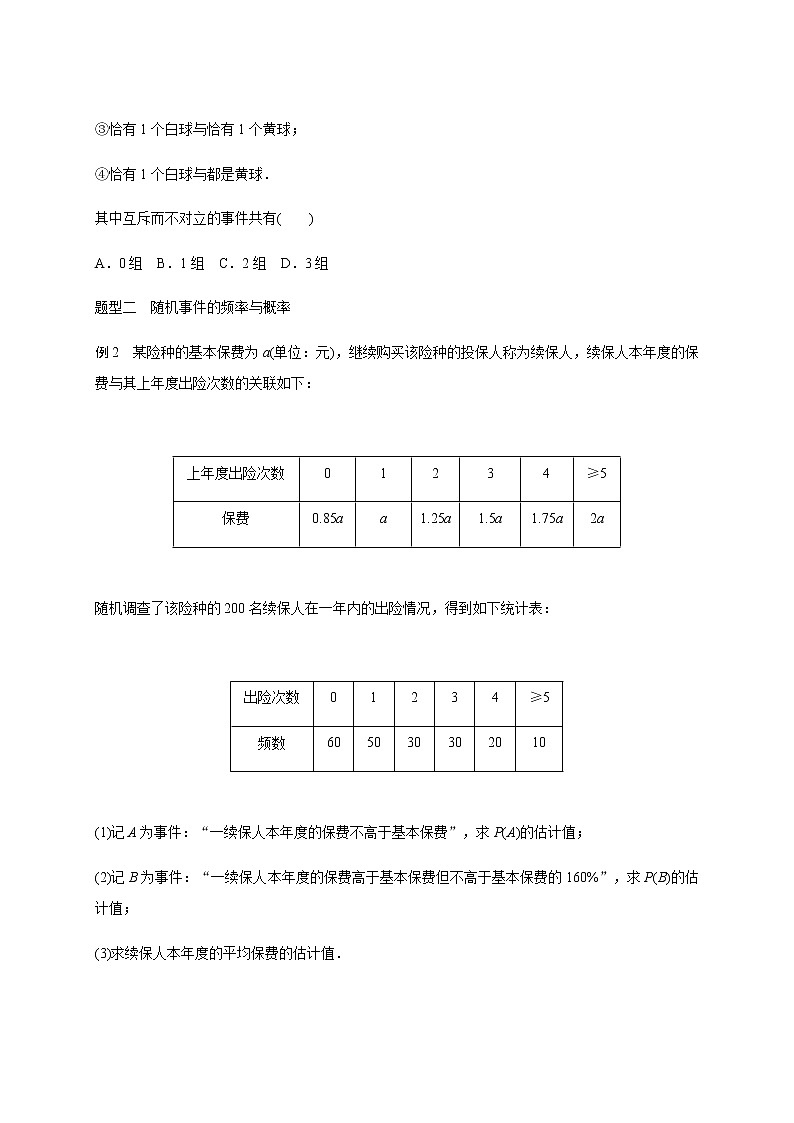
例2　某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：

(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；

(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；

(3)求续保人本年度的平均保费的估计值．

　某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买.

(1)估计顾客同时购买乙和丙的概率；

(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；

(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？

题型三　互斥事件、对立事件的概率

命题点1　互斥事件的概率

例3　袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，试求得到黑球、黄球和绿球的概率各是多少？

命题点2　对立事件的概率

例4　某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个．设1张奖券中特等奖，一等奖，二等奖的事件分别为A，B，C，求：

(1)P(A)，P(B)，P(C)；

(2)1张奖券的中奖概率；

(3)1张奖券不中特等奖且不中一等奖的概率．

　经统计，在某储蓄所一个营业窗口等候的人数相应的概率如下：

求：(1)至多2人排队等候的概率；

(2)至少3人排队等候的概率．

1．概率和频率

(1)在相同的条件S下重复n次试验，观察某一事件A是否出现，称n次试验中事件A出现的次数nA为事件A出现的频数，称事件A出现的比例fn(A)＝为事件A出现的频率．

(2)对于给定的随机事件A，在相同条件下，随着试验次数的增加，事件A发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画随机事件A发生的可能性大小，并把这个常数称为随机事件A的概率，记作P(A)．

2．事件的关系与运算

3.概率的几个基本性质

(1)概率的取值范围：0≤P(A)≤1.

(2)必然事件的概率P(E)＝1.

(3)不可能事件的概率P(F)＝0.

(4)概率的加法公式

如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B)．

(5)对立事件的概率

若事件A与事件B互为对立事件，则P(A)＝1－P(B)．

【知识拓展】

互斥事件与对立事件的区别与联系

互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件．

典例　某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.

已知这100位顾客中一次购物量超过8件的顾客占55%.

(1)确定x，y的值，并估计顾客一次购物的结算时间的平均值；

(2)求一位顾客一次购物的结算时间不超过2分钟的概率．(将频率视为概率)

1．从{1,2,3,4,5}中随机选取一个数a，从{1,2,3}中随机选取一个数b，则b>a的概率是(　　)

A.  B.  C.  D.

2．将一枚硬币向上抛掷10次，其中“正面向上恰有5次”是(　　)

A．必然事件   B．随机事件

C．不可能事件   D．无法确定

3．某射手在一次射击中，射中10环，9环，8环的概率分别为0.2,0.3,0.1，则此射手在一次射击中不超过8环的概率为(　　)

A．0.5  B．0.3  C．0.6  D．0.9

4．袋中装有9个白球，2个红球，从中任取3个球，则①恰有1个红球和全是白球；②至少有1个红球和全是白球；③至少有1个红球和至少有2个白球；④至少有1个白球和至少有1个红球．在上述事件中，是对立事件的为________．

1．甲、乙两人下棋，两人下成和棋的概率是，甲获胜的概率是，则甲不输的概率为(　　)

A.   B.

C.   D.

2．袋中装有3个白球，4个黑球，从中任取3个球，则①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球．

在上述事件中，是对立事件的为(　　)

A．①  B．②  C．③  D．④

3．从一箱产品中随机地抽取一件，设事件A＝{抽到一等品}，事件B＝{抽到二等品}，事件C＝{抽到三等品}，且已知P(A)＝0.65，P(B)＝0.2，P(C)＝0.1，则事件“抽到的产品不是一等品”的概率为(　　)

A．0.7  B．0.65  C．0.35  D．0.5

4．有一个游戏，其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进，每人一个方向．事件“甲向南”与事件“乙向南”是(　　)

A．互斥但非对立事件   B．对立事件

C．相互独立事件   D．以上都不对

5．从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30,40]克的概率为0.5，那么重量不小于30克的概率为(　　)

A．0.8  B．0.5  C．0.7  D．0.3

6．从存放的号码分别为1,2,3，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：

则取到号码为奇数的卡片的频率是(　　)

A．0.53  B．0.5  C．0.47  D．0.37

7．在200件产品中，有192件一级品，8件二级品，则下列事件：

①在这200件产品中任意选出9件，全部是一级品；

②在这200件产品中任意选出9件，全部是二级品；

③在这200件产品中任意选出9件，不全是二级品．

其中________是必然事件；________是不可能事件；________是随机事件．

8．若随机事件A，B互斥，A，B发生的概率均不等于0，且P(A)＝2－a，P(B)＝4a－5，则实数a的取值范围是________________．

9．在5张卡片上分别写有数字1,2,3,4,5，然后将它们混合，再任意排列成一行，则得到的数能被2或5整除的概率是________．

10．一个口袋内装有大小相同的红球，白球和黑球，从中摸出一个球，摸出红球或白球的概率为0.58，摸出红球或黑球的概率为0.62，那么摸出红球的概率为________．

11．某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：

(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；

(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率．

12．国家射击队的队员为在射击世锦赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次命中7～10环的概率如下表所示：

求该射击队员射击一次：

(1)射中9环或10环的概率；

(2)命中不足8环的概率．

*13.一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：

(1)取出1球是红球或黑球的概率；

(2)取出1球是红球或黑球或白球的概率．