2022-2023学年广东省广州市黄埔军校中学八年级（上）期末数学试卷

2022-2023学年广东省广州市黄埔军校中学八年级（上）期末数学试卷

一、单选题（本大题共10小题，每小题3分，共30分）

1．（3分）据《央视网》2021年10月26日报道，我国成功研制出超导量子计算原型机“祖冲之二号”．截至报道时，根据已公开的最优经典算法，在处理“量子随机线路取样”问题时，全球其他最快的超级计算机用时2.3秒的计算量，“祖冲之二号”用时大约为0.00000023秒，将数字0.00000023用科学记数法表示应为　　

A． B． C． D．

2．（3分）下列变形是因式分解的是　　

A． B． 

C． D．

3．（3分）已知图中的两个三角形全等，则等于　　

A． B． C． D．

4．（3分）如果把分式中的，都扩大到原来的5倍，那么分式的值　　

A．扩大到原来的25倍 B．扩大到原来的5倍 

C．值不变 D．缩小为原来的

5．（3分）如图，点，，，在同一条直线上，点，在直线的两侧，，，添加下列哪个条件后，仍不能判定出　　

A． B． C． D．

6．（3分）下列计算正确的是　　

A． B． C． D．

7．（3分）下列长度的三条线段，能组成三角形的是　　

A．3，4，8 B．5，6，11 C．5，8，15 D．3，4，6

8．（3分）一个多边形的外角和等于，则这个多边形的边数为　　

A．3 B．4 C．5 D．以上均有可能

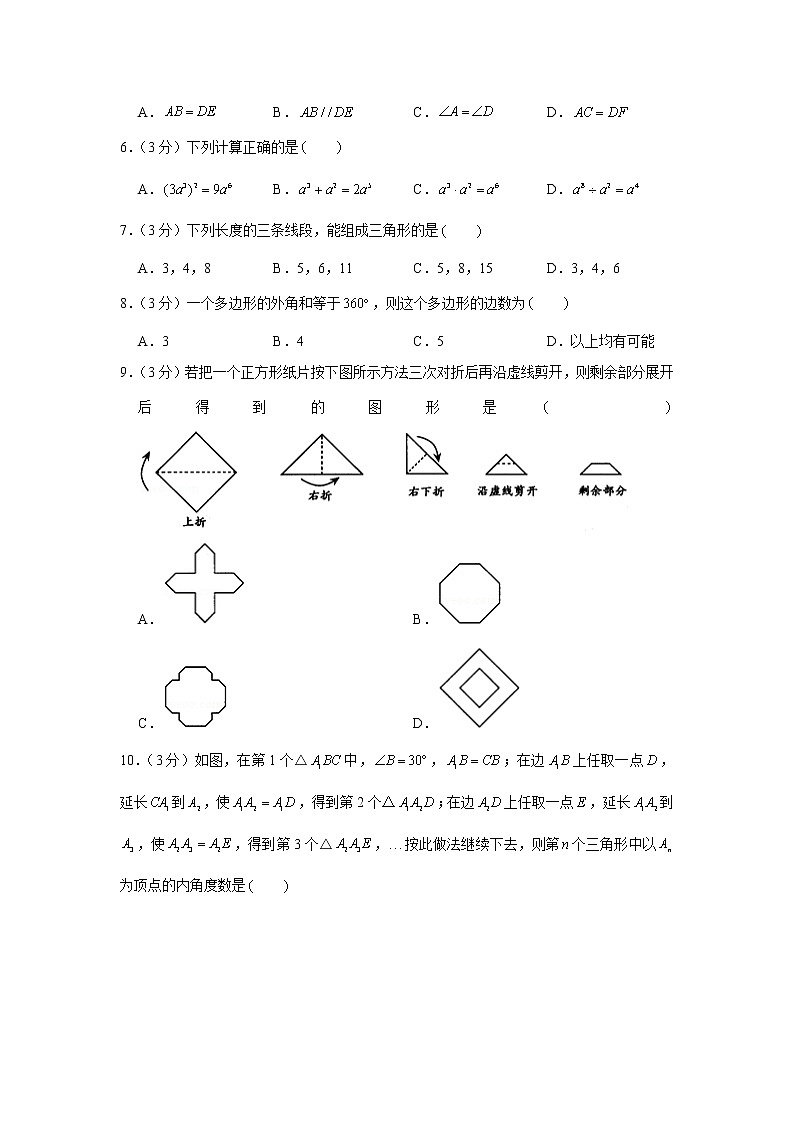
9．（3分）若把一个正方形纸片按下图所示方法三次对折后再沿虚线剪开，则剩余部分展开后得到的图形是　　

A． B． 

C． D．

10．（3分）如图，在第1个△中，，；在边上任取一点，延长到，使，得到第2个△；在边上任取一点，延长到，使，得到第3个△，按此做法继续下去，则第个三角形中以为顶点的内角度数是　　

A． B． C． D．

二、填空题（本大题共6小题，每小题3分，共18分）

11．（3分）已知点关于轴的对称点的坐标为，则点的坐标为 　　．

12．（3分）化简的结果是　　

13．（3分）如图，中，，是的中点，，，则的长为 　　．

14．（3分）若的展开式中不含有的一次项，则的值是 　　．若是一个完全平方式，则的值为 　　．

15．（3分）如图，等腰三角形的底边长为4，面积是16，腰的垂直平分线分别交，边于，点．若点为边的中点，点为线段上一动点，则的最小值为 　　．

16．（3分）如图，在中，，于点，于点，连接，，下列结论中：①；②；③；④若，则．正确的有　　（填序号）．

三、解答题（本大题共7小题，共52分）

17．（4分）分解因式：

（1）；

（2）．

18．（6分）如图，在中，．

（1）作的垂直平分线，交于点，交于点（尺规作图，不写作法，保留作图痕迹）；

（2）当，时，求的周长．

19．（6分）如图：在等边三角形中，点、分别是、延长线上的点，且．求证：．

20．（8分）（1）先化简，再求值：，其中．

（2）解方程：．

21．（8分）星期天，小明和小军在同一小区门口同时出发，沿相同路线去离该小区1800米的青少年宫参加羽毛球训练，为响应“节能环保，绿色出行”的号召，两人都步行前往．已知小明的速度是小军的速度的1.2倍，小明比小军提前6分钟到达，求两人的速度．

22．（10分）如图1，有型、型、型三种不同形状的纸板，型是边长为的正方形，型是边长为的正方形，型是长为，宽为的长方形．现用型纸板一张，型纸板一张，型纸板两张拼成如图2的大正方形．

（1）观察图2，请你用两种方法表示出图2的总面积．

方法　　；

方法　　；

请利用图2的面积表示方法，写出一个关于，的等式：　　．

（2）已知图2的总面积为49，一张型纸板和一张型纸板的面积之和为25，求的值．

（3）用一张型纸板和一张型纸板，拼成图3所示的图形，若，，求图3中阴影部分的面积．

23．（10分）如图，在等边外作射线，，点关于直线的对称点为，连接，，其中，分别交射线于点，．

（1）①依题意补全图形；

②求的度数；

（2）用等式表示线段，与之间的数量关系，并证明．

（3）若是等腰三角形，直接写出的度数．

2022-2023学年广东省广州市黄埔军校中学八年级（上）期末数学试卷

参考答案与试题解析

一、单选题（本大题共10小题，每小题3分，共30分）

1．（3分）据《央视网》2021年10月26日报道，我国成功研制出超导量子计算原型机“祖冲之二号”．截至报道时，根据已公开的最优经典算法，在处理“量子随机线路取样”问题时，全球其他最快的超级计算机用时2.3秒的计算量，“祖冲之二号”用时大约为0.00000023秒，将数字0.00000023用科学记数法表示应为　　

A． B． C． D．

【分析】科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数．

【解答】解：．

故选：．

【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，正确确定的值以及的值是解决问题的关键．

2．（3分）下列变形是因式分解的是　　

A． B． 

C． D．

【分析】根据因式分解是把一个多项式转化成几个整式乘积的形式，可得答案．

【解答】解：、是整式的乘法，故错误；

、把一个多项式转化成几个整式乘积的形式，故正确；

、没把一个多项式转化成几个整式乘积的形式，故错误；

、没把一个多项式转化成几个整式乘积的形式，故错误；

故选：．

【点评】本题考查了因式分解的意义，因式分解是把一个多项式转化成几个整式乘积的形式，注意因式分解与整式乘法的区别．

3．（3分）已知图中的两个三角形全等，则等于　　

A． B． C． D．

【分析】根据已知数据找出对应角，根据全等得出，，根据三角形内角和定理求出即可．

【解答】解：

和全等，，，

，，，

，

故选：．

【点评】本题考查了三角形内角和定理，全等三角形的性质的应用，能根据全等三角形的性质得出，是解此题的关键，注意：全等三角形的对应边相等，对应角相等．

4．（3分）如果把分式中的，都扩大到原来的5倍，那么分式的值　　

A．扩大到原来的25倍 B．扩大到原来的5倍 

C．值不变 D．缩小为原来的

【分析】根据分式的基本性质即可求出答案．

【解答】解：原式，

故选：．

【点评】本题考查分式的基本性质，解题的关键是熟练运用分式的基本性质，本题属于基础题型．

5．（3分）如图，点，，，在同一条直线上，点，在直线的两侧，，，添加下列哪个条件后，仍不能判定出　　

A． B． C． D．

【分析】先根据平行线的性质得到，再证明，然后根据全等三角形的判定方法对各选项进行判断．

【解答】解：，

，

，

，

即，

当添加，即时，可根据“”判断；

当添加时，可根据“”判断；

当添加时，可根据“”判断．

故选：．

【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法，选用哪一种方法，取决于题目中的已知条件．

6．（3分）下列计算正确的是　　

A． B． C． D．

【分析】利用合并同类项的法则，积的乘方的法则，同底数幂的乘法的法则，同底数幂的除法的法则对各项进行运算即可．

【解答】解：、，故符合题意；

、与不属于同类项，不能合并，故不符合题意；

、，故不符合题意；

、，故不符合题意；

故选：．

【点评】本题主要考查合并同类项，积的乘方，同底数幂的乘法，同底数幂的除法，解答的关键是对相应的运算法则掌握．

7．（3分）下列长度的三条线段，能组成三角形的是　　

A．3，4，8 B．5，6，11 C．5，8，15 D．3，4，6

【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．

【解答】解：根据三角形的三边关系，得，

、，不能组成三角形，不符合题意；

、，不能够组成三角形，不符合题意；

、，不能组成三角形，不符合题意；

、，能够组成三角形，符合题意．

故选：．

【点评】此题考查了三角形的三边关系．判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数．

8．（3分）一个多边形的外角和等于，则这个多边形的边数为　　

A．3 B．4 C．5 D．以上均有可能

【分析】根据多边形的外角和等于判断即可．

【解答】解：多边形的外角和等于，

这个多边形的边数不能确定．

故选：．

【点评】本题考查了多边形的外角和定理，解题的关键是明确多边形的外角和与边数无关，任何多边形的外角和都是．

9．（3分）若把一个正方形纸片按下图所示方法三次对折后再沿虚线剪开，则剩余部分展开后得到的图形是　　

A． B． 

C． D．

【分析】拿正方形纸片先沿对角线向上翻折，再向右翻折，右下翻折，剪去上面一个等腰直角三角形，展开即可得到正确答案．

【解答】解：动手操作后可得第一个图案．

故选：．

【点评】本题主要考查了剪纸问题；主要是让学生学会动手操作能力．

10．（3分）如图，在第1个△中，，；在边上任取一点，延长到，使，得到第2个△；在边上任取一点，延长到，使，得到第3个△，按此做法继续下去，则第个三角形中以为顶点的内角度数是　　

A． B． C． D．

【分析】先根据等腰三角形的性质求出的度数，再根据三角形外角的性质及等腰三角形的性质分别求出，及的度数，找出规律即可得出第个三角形中以为顶点的底角度数．

【解答】解：在中，，，

，

，是△的外角，

；

同理可得，，

第个三角形中以为顶点的底角度数是．

故选：．

【点评】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出，及的度数，找出规律是解答此题的关键．

二、填空题（本大题共6小题，每小题3分，共18分）

11．（3分）已知点关于轴的对称点的坐标为，则点的坐标为 　　．

【分析】根据关于轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点关于轴的对称点的坐标是，进而得出答案．

【解答】解：点关于轴的对称点的坐标为，

点的坐标为：．

故答案为：．

【点评】此题主要考查了关于轴对称点的性质，正确记忆关于坐标轴对称点的性质是解题关键．

12．（3分）化简的结果是　　

【分析】直接利用分式加减运算法则计算得出答案．

【解答】解：

．

故答案为：．

【点评】此题主要考查了分式的加减运算，正确掌握运算法则是解题关键．

13．（3分）如图，中，，是的中点，，，则的长为 　9　．

【分析】先根据是的中点得出，然后根据角所对的直角边等于斜边的一半得出，进而求出的长．

【解答】解：是的中点，，

．

中，，，

，

．

故答案为：9．

【点评】本题考查了三角形的中线：三角形一边的中点与此边所对顶点的连线叫做三角形的中线．也考查了含角的直角三角形的性质，求出与是解题的关键．

14．（3分）若的展开式中不含有的一次项，则的值是 　2　．若是一个完全平方式，则的值为 　　．

【分析】原式利用多项式乘多项式法则计算，根据结果不含的一次项，确定出的值即可；利用完全平方公式的结构特征确定出的值即可．

【解答】解：

，

展开式中不含有的一次项，

，

解得：；

是一个完全平方式，

，

．

故答案案为：2；．

【点评】此题考查了完全平方式，以及多项式乘多项式，熟练掌握运算法则及完全平方公式是解本题的关键．

15．（3分）如图，等腰三角形的底边长为4，面积是16，腰的垂直平分线分别交，边于，点．若点为边的中点，点为线段上一动点，则的最小值为 　8　．

【分析】连接，由于是等腰三角形，点是边的中点，故，根据三角形的面积公式求出的长，再根据是线段的垂直平分线可知，点关于直线的对称点为点，故的长为的最小值．

【解答】解：连接，

是等腰三角形，点是边的中点，

，

，

解得，

是线段的垂直平分线，

点关于直线的对称点为点，

的长为的最小值8．

故答案为：8．

【点评】本题考查的是轴对称最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．

16．（3分）如图，在中，，于点，于点，连接，，下列结论中：①；②；③；④若，则．正确的有　①②④　（填序号）．

【分析】①②只要证明即可解决问题．③如图1中，作于，于，易证，四边形是正方形，想办法证明，即可．④如图2中，延长到，使得．连接、．想办法证明是等边三角形，即可解决问题．

【解答】解：，

，

，

，

在和中，

，

，

，，故①正确，

，

取的中点，连接、．

，

，

、、、四点共圆，

，故②正确，

如图1中，作于，于，易证，四边形是正方形，

，，

，

，

，即，故③错误，

如图2中，延长到，使得．连接、．

，，，

，，

，

，

，

，

是等边三角形，

，

，

，

，

，

，

，

，

，

，

，故④正确，

故答案为：①②④．

【点评】本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、等边三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造特殊三角形解决问题，属于中考选择题中的压轴题．

三、解答题（本大题共7小题，共52分）

17．（4分）分解因式：

（1）；

（2）．

【分析】（1）先提取公因式，然后再利用平方差公式继续分解即可；

（2）先提取公因式，然后再利用完全平方公式继续分解即可．

【解答】解：（1）

；

（2）

．

【点评】本题考查了因式分解十字相乘法，提取公因式与公式法的综合运用，一定要注意如果多项式的各项有公因式，必须先提取公因式，然后再继续分解．

18．（6分）如图，在中，．

（1）作的垂直平分线，交于点，交于点（尺规作图，不写作法，保留作图痕迹）；

（2）当，时，求的周长．

【分析】（1）利用基本作图作垂直平分；

（2）根据线段垂直平分线的性质得到，然后利用等线段代换得到的周长．

【解答】解：（1）如图，为所作；

（2）垂直平分，

，

的周长．

【点评】本题考查了作图基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了线段垂直平分线的性质．

19．（6分）如图：在等边三角形中，点、分别是、延长线上的点，且．求证：．

【分析】证明，证明，则结论得证．

【解答】证明：等边三角形

，

，

，

在和中，

，

  ，

．

【点评】本题考查了等边三角形的性质及全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键．

20．（8分）（1）先化简，再求值：，其中．

（2）解方程：．

【分析】（1）先把括号内通分和除法运算化为乘法运算，再约分得到原式，然后把代入计算即可；

（2）先把方程两边乘以得到整式方程，再解整式方程，然后进行检验确定原方程的解．

【解答】解；（1）原式

，

当时，原式；

（2）去分母得，

解得，

检验：当时，，则为原方程的解，

所以原方程的解为．

【点评】本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值．也考查了解分式方程．

21．（8分）星期天，小明和小军在同一小区门口同时出发，沿相同路线去离该小区1800米的青少年宫参加羽毛球训练，为响应“节能环保，绿色出行”的号召，两人都步行前往．已知小明的速度是小军的速度的1.2倍，小明比小军提前6分钟到达，求两人的速度．

【分析】设小军的速度是米分，则小明速度是米分，由题意：沿相同路线去离该小区1800米的青少年宫参加羽毛球训练，小明比小军提前6分钟到达，列出分式方程，解方程即可．

【解答】解：设小军的速度是米分，则小明速度是米分，

依题意得：，

解得：，

经检验，是原方程的解，且符合题意，

则，

答：小军的速度是50米分，小明的速度是60米分．

【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．

22．（10分）如图1，有型、型、型三种不同形状的纸板，型是边长为的正方形，型是边长为的正方形，型是长为，宽为的长方形．现用型纸板一张，型纸板一张，型纸板两张拼成如图2的大正方形．

（1）观察图2，请你用两种方法表示出图2的总面积．

方法　　；

方法　　；

请利用图2的面积表示方法，写出一个关于，的等式：　　．

（2）已知图2的总面积为49，一张型纸板和一张型纸板的面积之和为25，求的值．

（3）用一张型纸板和一张型纸板，拼成图3所示的图形，若，，求图3中阴影部分的面积．

【分析】（1）由观察图2可得两种方法表示出图2的总面积为和，关于，的等式；

（2）由题意得，，，两个等式作差可求得此题结果；

（3）由题意得，从而可解得此题结果．

【解答】解：（1）用两种方法表示出图2的总面积为和，

关于，的等式，

故答案为：，，；

（2）由题意得，，，

；

（3）由题意得图3中阴影部分的面积为：，

当，时，

图3中阴影部分的面积为：．

【点评】此题考查了完全平方公式几何背景的应用能力，关键是能根据图形准确列式，并灵活运用完全平方公式进行变式应用．

23．（10分）如图，在等边外作射线，，点关于直线的对称点为，连接，，其中，分别交射线于点，．

（1）①依题意补全图形；

②求的度数；

（2）用等式表示线段，与之间的数量关系，并证明．

（3）若是等腰三角形，直接写出的度数．

【分析】（1）①根据题意画出图形即可；

②点关于直线的对称点为，得到，设，则，用的代数式表示即可解决问题．

（2）结论：．如图1中，连接，在上取一点，使得，连接．证明，可得结论．

（3）分二种情形：①如图中，当时．②如图中，当时，利用等腰三角形的性质求解即可．

【解答】解：（1）①图形如图所示：

②连接，，关于对称，

，

可以假设，则，

，

，

，

．

．

（2）结论：．

理由：如图1中，连接，在上取一点，使得，连接．

，关于对称，

，，

，

，，

，

是等边三角形，

，，

是等边三角形，

，，

，

在和中，

，

，

，

，

．

（3）①如图中，当时，．

②如图中，当时，．

综上所述的值为：，．

【点评】本题是几何变换综合题，考查了作图轴对称变换，全等三角形的判定和性质，等边三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．