河南省周口市川汇区2022-2023学年八年级上学期期末数学试题

河南省周口市川汇区2022-2023学年八年级上学期期末数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．用三根长分别为的小木棒首尾相接拼成一个三角形，则a可能是（    ）

A．1 B．2 C．3 D．4

【答案】D

【分析】根据三角形的三边关系进行计算即可得．

【详解】解：∵三根长分别为的小木棒首尾相接拼成一个三角形，

∴，

，

故选：D．

【点睛】本题考查了三角形的三边关系，解题的关键是掌握三角形的三边关系．

2．如图，在四边形ABCD中，对角线AC平分，下列条件中不能保证的是（    ）

A． B． C． D．

【答案】C

【分析】按照全等三角形的判定方法逐一判断即可．

【详解】∵AC平分

∴，

A.对于，，，利用可以证明；

B.对于，，，利用可以证明；

C.对于，，，不能证明；

D.对于，，利用可以证明；

故选C．

【点睛】本题考查全等三角形的判定定理，熟练掌握三角形全等的条件是解题的关键．

3．在平面直角坐标系中，点P与点A关于x轴对称，点P与点B关于y轴对称．已知点，则点A的坐标是（    ）

A． B． C． D．

【答案】B

【分析】关于x轴对称，横坐标不变，纵坐标互为相反数；关于y轴对称，横坐标不变，纵坐标互为相反数．

【详解】∵点P与点关于y轴对称，

∴点坐标为

又∵点P与点A关于x轴对称，

∴点A的坐标是

故选B．

【点睛】本题考查关于x轴、y轴对称点的坐标规律，关键是熟练掌握点的变化规律．

4．下列运算正确的是（    ）

A． B． C． D．

【答案】B

【分析】根据合并同类项，积的乘方，同底数幂的除法和单项式乘以单项式法则依次运算判断．

【详解】A．不能合并，故错误；

B．，故正确；

C．，故错误；

D．，故错误．

故选B．

【点睛】本题考查了合并同类项，积的乘方，同底数幂的除法和单项式乘以单项式，熟练掌握各自的运算法则是解题的关键．

5．方程的实数根是（    ）

A．1 B． C．2 D．

【答案】D

【分析】运用平方差公式计算，然后解方程即可求解．

【详解】解：

即

解得：

故选D．

【点睛】本题考查解方程，运用平方差公式进行计算是解题的关键．

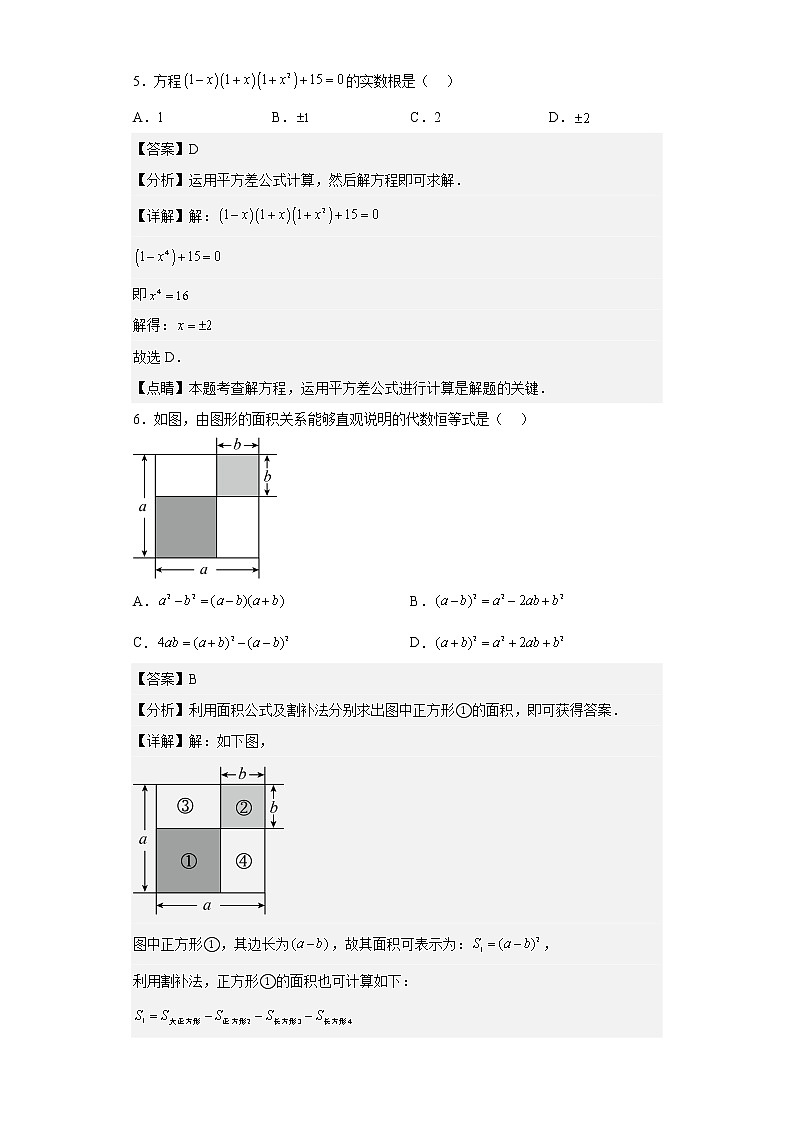
6．如图，由图形的面积关系能够直观说明的代数恒等式是（    ）

A． B．

C． D．

【答案】B

【分析】利用面积公式及割补法分别求出图中正方形①的面积，即可获得答案．

【详解】解：如下图，

图中正方形①，其边长为，故其面积可表示为：，

利用割补法，正方形①的面积也可计算如下：

，

即有．

故选：B．

【点睛】本题主要考查了完全平方公式与几何图形，理解并掌握完全平方公式是解题关键．

7．如图，点D，E分别在的AB，BC边上，将沿DE对折，使点B与点C重合，DE为折痕，若，则的值是（    ）

A． B． C． D．

【答案】C

【分析】由折叠的性质得出，设，由三角形的外角的性质求出，再由可得，则可得．最后列方程求解即可．

【详解】解：∵将沿折叠，使点B与点C重合，

∴，

∴，

设，

∴，

∵，

∴，

∴，

∵

∴

解得：，

∴，

故选：C．

【点睛】本题考查了折叠的性质，等腰三角形的性质及三角形的外角性质，利用折叠的性质及三角形的外角性质，理解等腰三角形的性质解题的关键．

8．要使分式有意义，字母x需要满足（    ）

A． B． C． D．且

【答案】D

【分析】要使分式有意义，分式的分母不为0，列不等式求解即可．

【详解】解：要使分式有意义，

，

即，

解得且，

故选：D．

【点睛】本题主要考查分式有意义；熟记分式有意义的条件是解题的关键．

9．据报道：芯片被誉为现代工业的掌上明珠，芯片制造的核心是光刻技术，我国的光刻技术水平已突破到．已知，则用科学记数法表示是（    ）

A． B． C． D．

【答案】C

【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【详解】解：∵，

∴28nm=2.8×10-8m．

故选：C．

【点睛】本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

10．如图，在中，，点D为边的中点，点P在边上，，则的最小值等于（    ）

A．5 B．6 C．7 D．8

【答案】B

【分析】作点D关于的对称点E，连接，，，根据对称性可知：，，当B，P，E在同一直线上时，，再判断是等边三角形，根据三角函数求出，即可求出的最小值．

【详解】如图所示，作点D关于的对称点E，连接，，，

根据对称性可知：，，

∴，

∴当B，P，E在同一直线上时，

，

∵，点D关于的对称点E，，

∴

∴，

∴是等边三角形，

∴，

又∵D为上的中点，

∴，

，

，

∴，

∵，，

∴，

∴，

∴，

即的最小值为6，

故选：B．

【点睛】本题考查轴对称的最短路线问题，等边三角形的性质，解题的关键是利用轴对称变换来解决，作点关于某直线的对称点．

二、填空题

11．的面积为，边长为，则高为_________．

【答案】

【分析】根据三角形的面积公式，即可求解．

【详解】解：∵的面积为，边长为，

∴高为．

故答案为：

【点睛】本题主要考查了列代数式，熟练掌握三角形的面积公式是解题的关键．

12．观察算式找规律：①；②；③；④…．第n个式子是_____________．

【答案】

【分析】观察算式的左边，偶数乘以这个数加2，再加上1，右边为从3开始的连续的奇数的平方，据此即可求解．

【详解】解：①；

②；

③；

④

…，

第n个式子是：

故答案为：．

【点睛】本题考查了数字类规律，找到规律是解题的关键．

13．若等式恒成立，则_________．

【答案】4

【分析】利用多项式乘法将已知等式右边展开，然后合并同类项，与等式左边进行比较即可求解．

【详解】解：∵，

∴，

∴，，

∴，，

∴，

故答案为：4．

【点睛】此题主要考查了多项式乘以多项式，正确去括号得出是解题关键．

14．已知是分式方程的解，则_________．

【答案】

【分析】将代入方程求解即可．

【详解】解：将代入方程

得，，

解得，

经检验，是该分式方程的解，

故答案为．

【点睛】本题主要考查分式方程的解，分式方程是方程中的一种，且分母里含有未知数的(有理)方程叫做分式方程，等号两边至少有一个分母含有未知数．

15．如图，线段于点C，，则的面积之和等于_________．

【答案】14

【分析】由得，设，则，，由勾股定理求出x的值，根据直角三角形的面积求法，即可计算出面积和．

【详解】∵，

∴，

又∵，

∴，

则，

设，

则，，

在中，，

，

解得，

则

故答案为：14

【点睛】本题考查的是相似三角形的性质与判定，勾股定理，直角三角形的面积，解题的关键是由相似三角形得出三者间的数量关系．

三、解答题

16．（1）运用乘法公式计算：`；

（2）分解因式：；

【答案】（1）；（2）

【分析】（1）先分组，然后运用完全平方公式进行解题；

（2）先运用多项式的乘法进行解题，然后因式分解即可．

【详解】（1）原式

（2）原式．

【点睛】本题考查整式乘法公式和因式分解，掌握完全平方公式是解题的关键．

17．先化简，再求值：，其中x的值从，，，中选取．

【答案】，

【分析】根据分式的混合运算化简，然后根据分式有意义的条件取舍的值，代入化简后的式子即可求解．

【详解】解：原式

∵x不能取，0，1，

∴．

∴原式．

【点睛】本题考查了分式的化简求值，分式有意义的条件，掌握分式的混合运算是解题的关键．

18．解分式方程：

(1)．

(2)

【答案】(1)

(2)原分式方程无解

【分析】（1）方程两边同时乘以，把分式方程化为整式方程，解整式方程检验后，即可得出分式方程的解；

（2）方程两边同时乘以，把分式方程化为整式方程，解整式方程检验后，即可得出分式方程的解．

【详解】（1）解：方程两边乘，得．

解得．

检验：当时，．

所以，原分式方程的解为．

（2）方程两边乘，得．

解得．

检验：当时，，因此不是原分式方程的解．

所以，原分式方程无解．

【点睛】本题考查了解分式方程，去分母把分式方程化为整式方程是解决问题的关键．

19．如图，在中，点D在边BC的延长线上，射线CE在的内部．给出下列信息：①；②CE平分：③．请选择其中的两条信息作为条件，余下的一条信息作为结论组成一个命题．试判断这个命题是否正确，并说明理由．

【答案】见解析

【分析】选择①②作为条件，③作为结论；由平行线的性质可以得到，由角平分线可以得到，等量代换可证，进而证明结论．

【详解】选择①②作为条件，③作为结论．

∵，

∴．

∵CE平分，

∴．

∴．

∴．

【点睛】本题考查等腰三角形的判定，熟练掌握等腰三角形的判定是解题的关键．

20．某中学为了让学生体验农耕劳动，开辟了一处耕种园，需要采购一批蜜薯秧苗开展种植活动．据了解，市场上每捆蜜薯秧苗的价格是农科基地的1.25倍，用320元在市场上购买的蜜薯秧苗比在农科基地购买的少4捆．求农科基地每捆蜜薯秧苗的价格．

【答案】农科基地每捆蜜薯秧苗的价格是16元

【分析】设农科基地每捆蜜薯秧苗的价格为x元，根据用320元在市场上购买的蜜薯秧苗比在农科基地购买的少4捆列分式方程解题即可．

【详解】设农科基地每捆蜜薯秧苗的价格为x元，则市场上每捆蜜薯秧苗的价格为元．

根据购买捆数关系，得

方程两边乘，得，

解得．

检验：当时，．

所以，是原分式方程的解．

答：农科基地每捆蜜薯秧苗的价格是16元．

【点睛】本题考查分式方程的应用，解题时注意分式方程要验根．

21．如图，已知锐角．

(1)尺规作图．作AC边的垂直平分线交BC于点D；（不写作法，保留作图痕迹）

(2)若与有什么关系?并说明理由．

【答案】(1)见解析

(2)，理由见解析

【分析】（1）分别以点A、C为圆心，以大于为半径画弧，在的两边相交于两点，然后过两交点作直线即可；

（2）如图：连接AD．根据垂直平分线的性质可得，进而得到；然后再说明可得，最后再根据三角形外角的性质即可解答．

【详解】（1）解：如图：

（2）解：．理由如下：

连接AD．

∵点D在AC的垂直平分线上，

∴．

∴．

∵，

∴．

∴．

∵，

∴．

【点睛】本题主要考查了线段的垂直平分线、等腰三角形的判定与性质、三角形的外角等知识点，正确作出垂直平分线是解答本题的关键．

22．操作实验．一张大小为1个单位面积的纸条，按照如下方法将它裁剪，第1次剪去纸条面积的，第2次剪去纸条剩余面积的，第3次剪去纸条剩余面积的，…，第n次剪去纸条剩余面积的．

(1)完成下表表格内容：

(2)由于减去的纸条面积与剩余的纸条面积之和等于面积总量，所以得关系式： ___________；

(3)计算，并逆用计算结果证明（2）中的等式．

【答案】(1)见解析

(2)

(3)

【分析】（1）根据题意，补全表格，即可求解；

（2）根据减去的纸条面积与剩余的纸条面积之和等于面积总量，即可求解；

（3）先计算，再代入（2）中式子，即可求解．

【详解】（1）解：根据题意，补全表格如下：

（2）解：根据题意得：第n次剪后剩余的面积为，

∴；

故答案为：

（3）解：，

【点睛】本题主要考查了数字类规律题，明确题意，准确得到规律是解题的关键．

23．综合与实践

在数学实验课上，老师让学生以“折叠筝形”为主题开展数学实践探究活动．

定义：两组邻边分别相等的四边形叫做“筝形”．

(1)概念理解

如图1，将一张纸对折压平，以折痕为边折出一个三角形，然后把纸展平，折痕为四边形．判断四边形的形状：_______________筝形（填“是”或“不是”）

(2)性质探究

如图2，已知四边形纸片是筝形，请用测量、折叠等方法猜想筝形的角、对角线有什么几何特征，然后写出一条性质并进行证明．

(3)拓展应用

如图3，是锐角的高，将沿AB边翻折后得到，将沿AC边翻折后得到，延长EB，FC交于点G．

①请写出图3中的“筝形”：____________；（写出一个即可）

②若，当是等腰三角形时，请直接写出的度数．

【答案】(1)是

(2)在筝形中较长的对角线平分较短的对角线所对的两个角，理由见解析

(3)①四边形；②的度数为或或

【分析】（1）根据题意得，，即可得四边形是筝形；

（2）连接，，根据四边形是筝形得，，利用SSS证明，得，，即可得平分，；

（3）①根据沿AB边翻折后得到得，可得，，即可得；②根据沿AC边翻折后得到得，可得，，即可得四边形是筝形，则，，根据得，，根据在筝形中较长的对角线平分较短的对角线所对的两个角得，根据四边形内角和为，得，当是等腰三角形时，有三种情况：①当时，，可得，根据平角得，根据是锐角的高得，即可得；②当时，，则，根据是锐角的高得，即可得；③当时，，即可得，根据是锐角的高得，即可得．

【详解】（1）解：∵四边形为对折后折出的三角形。

∴，，

∴四边形是筝形，

故答案为：是．

（2）性质：在筝形中较长的对角线平分较短的对角线所对的两个角，证明如下：

证明：如图所示，连接，，

∵四边形是筝形，

∴，，

在和中，

∴（SSS），

∴，，

∴平分，．

（3）解：①∵沿AB边翻折后得到，

∴，

∴，，

∴四边形是筝形，

故答案为：四边形；

②∵沿AC边翻折后得到，

∴，

∴，，

∴四边形是筝形，

∴，，

∵，

∴，，

∵在筝形中较长的对角线平分较短的对角线所对的两个角，

∴，

∵四边形内角和为，，

∴，

当是等腰三角形时，有三种情况：

①当时，，

∴，

∴，

∴，

∵是锐角的高，

∴，

∴；

②当时，

∴，

∴，

∵是锐角的高，

∴，

∴；

③当时，

∴，

∴，

∵是锐角的高，

∴，

∴；

综上，的度数为或或．

【点睛】本题考查了四边形的综合题，解题的关键是理解题意，掌握全等三角形的判定与性质，折叠的性质．