初中数学冀教版九年级下册29.5 正多边形与圆公开课ppt课件

这是一份初中数学冀教版九年级下册29.5 正多边形与圆公开课ppt课件，文件包含295正多边形与圆课件ppt、295正多边形和圆教案doc等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

1.了解正多边形和圆的有关概念.2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系. (重点)3.会应用正多边形和圆的有关知识解决实际问题.（难点）
问题：观看大屏幕上这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
问题1 什么叫做正多边形？
各边相等,各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？
不是，因为矩形不符合各边相等；
不是，因为菱形不符合各角相等；
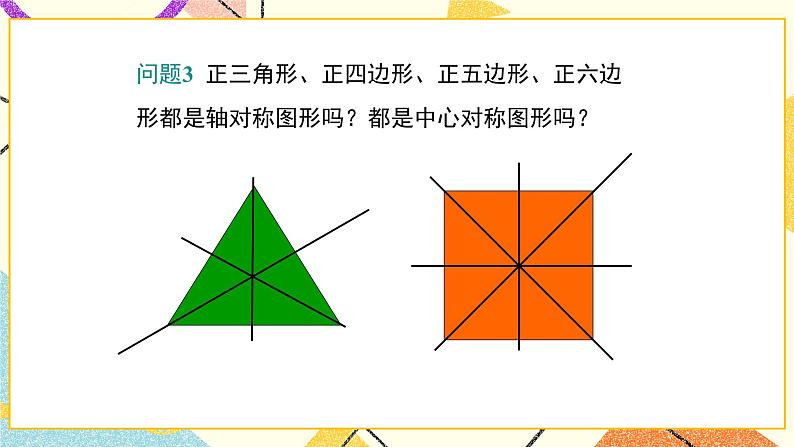
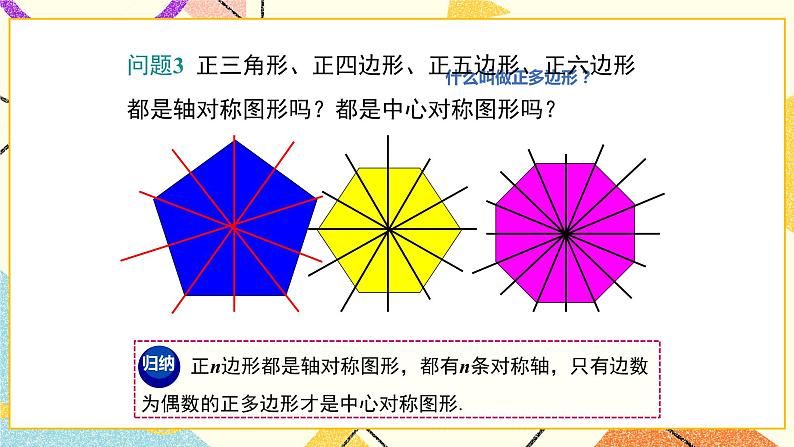
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称图形吗？
正n边形都是轴对称图形，都有n条对称轴，只有边数为偶数的正多边形才是中心对称图形.
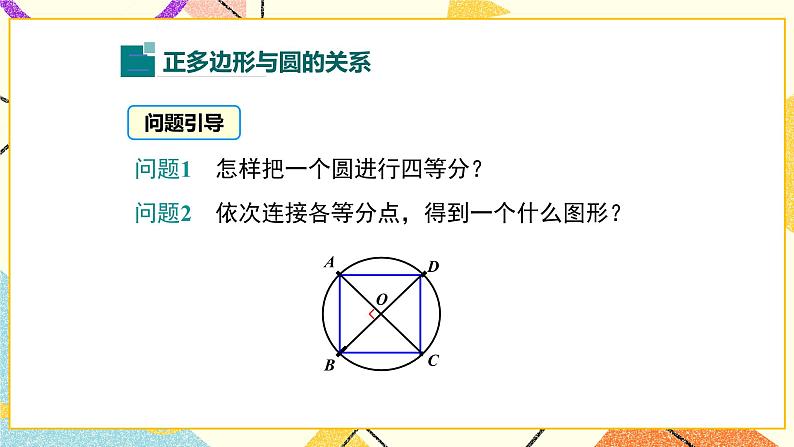
问题1 怎样把一个圆进行四等分？
问题2 依次连接各等分点，得到一个什么图形？
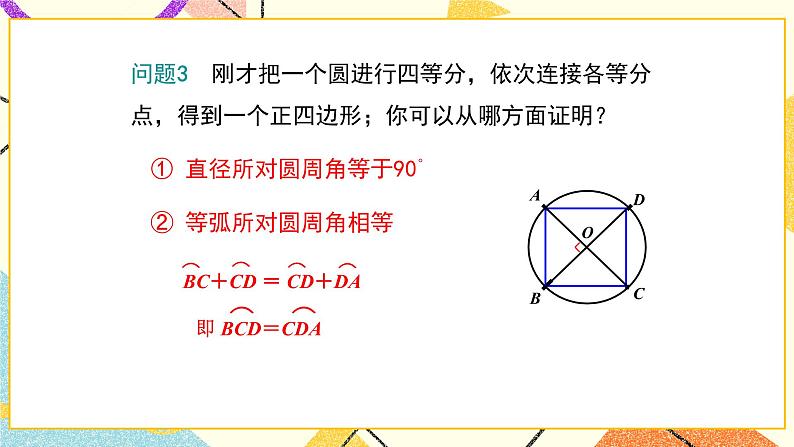
问题3 刚才把一个圆进行四等分，依次连接各等分点，得到一个正四边形；你可以从哪方面证明？
① 直径所对圆周角等于90°
② 等弧所对圆周角相等
③ ∠A ∠E
把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .(1)填空:
(2)这个五边形ABCDE是正五边形吗？简单说说理由.
像上面这样，只要把一个圆分成相等的一些弧，就可以作出这个圆的正多边形，这个圆就是这个正多形的外接圆，这个正多边形也称为这个圆的内接正多边形.
正多边形的外角=中心角
如图，已知半径为4的圆内接正六边形ABCDEF： ①它的中心角等于 度 ； ② OC BC (填＞、＜或＝）； ③△OBC是 三角形； ④圆内接正六边形的面积是 △OBC面积的 倍. ⑤圆内接正n边形面积公式:________________________.
例1：如图所示，正五边形ABCDE内接于⊙O，则∠ADE的度数是 （ ）A．60° B．45° C． 36° D． 30°
例2：有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (精确到0.1 m2).
利用勾股定理,可得边心距
解：过点O作OM⊥BC于M.
2.作边心距，构造直角三角形.
1.连半径，得中心角；
圆内接正多边形的辅助线
2. 若正多边形的边心距与半径的比为1:2，则这个多边形的边数是 .
5. 要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径
4.如图是一枚奥运会纪念币的图案，其形状近似看作为正七边形，则一个内角为 ___度.（不取近似值）
∴点P到各边距离之和=3BD=3×6=18．
解：过P作AB的垂线，分别交AB、DE于H、K，连接BD，作CG⊥BD于G.
∴P到AF与CD的距离之和，及P到EF、BC的距离之和均为HK的长.
∵六边形ABCDEF是正六边形∴AB∥DE，AF∥CD，BC∥EF，
∵BC=CD，∠BCD=∠ABC=∠CDE=120°，
∴∠CBD=∠BDC=30°，BD∥HK，且BD=HK.
∴BD=2BG=2×BC×cs∠CBD=6.
拓广探索如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.(1)求图①中∠MON=________; 图②中∠MON= ; 图③中∠MON= ;(2)试探究∠MON的度数与正n边形的边数n的关系.