

广东省深圳市2022年中考数学试卷【含答案】
展开2022年深圳市中考数学
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,共30分)
1. 下列互为倒数的是( )
A. 和 B. 和 C. 和 D. 和
2. 下列图形中,主视图和左视图一样的是( )
A. B. C. D.
3. 某学校进行演讲比赛,最终有7位同学进入决赛,这七位同学的评分分别是:9.5,9.3,9.1,9.4,9.7,9.3,9.6.请问这组评分的众数是( )
A. 9.5 B. 9.4 C. 9.1 D. 9.3
4. 某公司一年的销售利润是1.5万亿元.1.5万亿用科学记数法表示( )
A. B. C. D.
5. 下列运算正确的是( )
A. B. C. D.
6. 一元一次不等式组的解集为( )
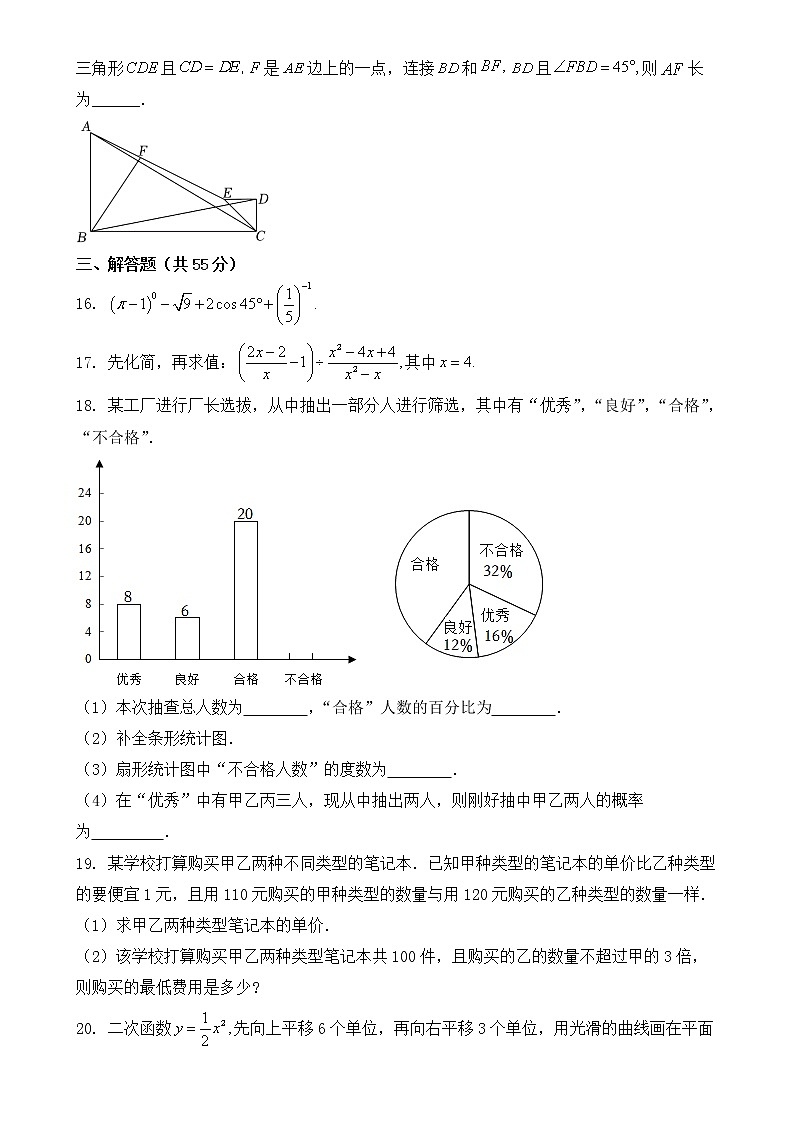
A. B.
C. D.
7. 将一副三角板如图所示放置,斜边平行,则的度数为( )
A. B. C. D.
8. 下列说法错误的是( )
A. 对角线垂直且互相平分的四边形是菱形 B. 同圆或等圆中,同弧对应的圆周角相等
C. 对角线相等的四边形是矩形 D. 对角线垂直且相等的平行四边形是正方形
9. 张三经营了一家草场,草场里面种植上等草和下等草.他卖五捆上等草的根数减去11根,就等于七捆下等草的根数;卖七捆上等草的根数减去25根,就等于五捆下等草的根数.设上等草一捆为根,下等草一捆为根,则下列方程正确的是( )
A B. C. D.
10. 如图所示,已知三角形为直角三角形,,BC为切线,为切点,则和面积之比为( )
A B. C. D.
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
11. 分解因式:=____.
12. 某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么则该工厂1200人中符合选拔条件的人数为________________.
13. 已知一元二次方程有两个相等的实数根,则的值为________________.
14. 如图,已知直角三角形中,,将绕点点旋转至的位置,且在的中点,在反比例函数上,则的值为________________.
15. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为______.
三、解答题(共55分)
16.
17. 先化简,再求值:其中
18. 某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.
(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
19. 某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜1元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.
(1)求甲乙两种类型笔记本的单价.
(2)该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?
20. 二次函数先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.
(1)的值为 ;
(2)在坐标系中画出平移后的图象并求出与的交点坐标;
(3)点在新的函数图象上,且两点均在对称轴的同一侧,若则 (填“”或“”或“”)
21. 一个玻璃球体近似半圆为直径,半圆上点处有个吊灯的中点为
(1)如图①,为一条拉线,在上,求的长度.
(2)如图②,一个玻璃镜与圆相切,为切点,为上一点,为入射光线,为反射光线,求的长度.
(3)如图③,是线段上的动点,为入射光线,为反射光线交圆于点在从运动到的过程中,求点的运动路径长.
22. (1)【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
(2)【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(3)【拓展应用】如图③,在菱形中,,为边上的三等分点,将沿翻折得到,直线交于点求的长.
参考答案
1. A.2. D.3. D.4. B.5. A.6. D.7. C.8. C.9. C10.B.
11. . 12. 900人 13. 9 14. 15. 16.
17. ,
18. 解:本次抽查的总人数为(人,“合格”人数的百分比为,故答案为:50人,;解:不合格的人数为:;补全图形如下:
【3解】解:扇形统计图中“不合格”人数的度数为,故答案为:;
解:列表如下:
| 甲 | 乙 | 丙 |
甲 |
| (乙,甲) | (丙,甲) |
乙 | (甲,乙) |
| (丙,乙) |
丙 | (甲,丙) | (乙,丙) |
|
由表知,共有6种等可能结果,其中刚好抽中甲乙两人的有2种结果,所以刚好抽中甲乙两人的概率为.
19. (1)甲类型的笔记本电脑单价为11元,乙类型的笔记本电脑单价为12元
(2)最低费用为1100元
20.【1】解:当时,,∴.
【2解】平移后的图象如图所示:
由题意得:,解得,当时,,则交点坐标为:,当时,,则交点坐标为:,综上所述:与的交点坐标分别为和.
【3】由平移后的二次函数可得:对称轴,,
∴当时,随x的增大而减小,当时,随x的增大而增大,
∴当P,Q两点均在对称轴的左侧时,若,则,
当P,Q两点均在对称轴的右侧时,若,则,
综上所述:点在新函数图象上,且P,Q两点均在对称轴同一侧,若,则或, 21. (1)2 (2) (3)
22. 证明:(1)将沿翻折到处,四边形是正方形,
,,,
,,;
(2)解:延长,交于,如图:
设,
在中,,,
解得,,
,,,
,即,,,
,,,,
,即,,
设,则,
,
,,即,
解得,的长为;
(3)(Ⅰ)当时,延长交于,过作于,如图:
设,,则,
,,,,
沿翻折得到,,,,
是的角平分线,,即①,
,,,,
在中,,②,
联立①②可解得,;
(Ⅱ)当时,延长交延长线于,过作交延长线于,如图:
同理,
,即,由得:,可解得,
,综上所述,的长为或.
2023年广东省深圳市中考适应性数学试卷(含答案): 这是一份2023年广东省深圳市中考适应性数学试卷(含答案),共23页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
2008年广东省深圳市中考数学试卷: 这是一份2008年广东省深圳市中考数学试卷,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2005年广东省深圳市中考数学试卷: 这是一份2005年广东省深圳市中考数学试卷,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。











