2023年中考数学一轮复习《平行四边形》课时练习（含答案）

2023年中考数学一轮复习

《平行四边形》课时练习

一              、选择题

1.如图，下列哪组条件不能判定四边形ABCD是平行四边形(　　)

A.AB∥CD，AB＝CD         B.AB∥CD，AD∥BC

C.OA＝OC，OB＝OD         D.AB∥CD，AD＝BC

2.在四边形ABCD中，AC，BD交于点O，且OA＝OC，OB＝OD，则下列结论不一定成立的是(    )

A.AB∥CD    B.BC∥AD      C.AB＝AD    D.BC＝AD

3.如图，▱OABC的顶点O、A、C的坐标分别是(0，0)，(2，0)，(0.5，1)，则点B坐标是(　　)

A.(1，2)      B.(0.5，2)     C.(2.5，1)    D.(2，0.5)

4.如图，▱ABCD的对角线AC，BD相交于O，EF过点O与AD，BC分别相交于E，F，若AB＝4，BC＝5，OE＝1.5，那么四边形EFCD的周长为(     )

A.16          B.14             C.12           D.10

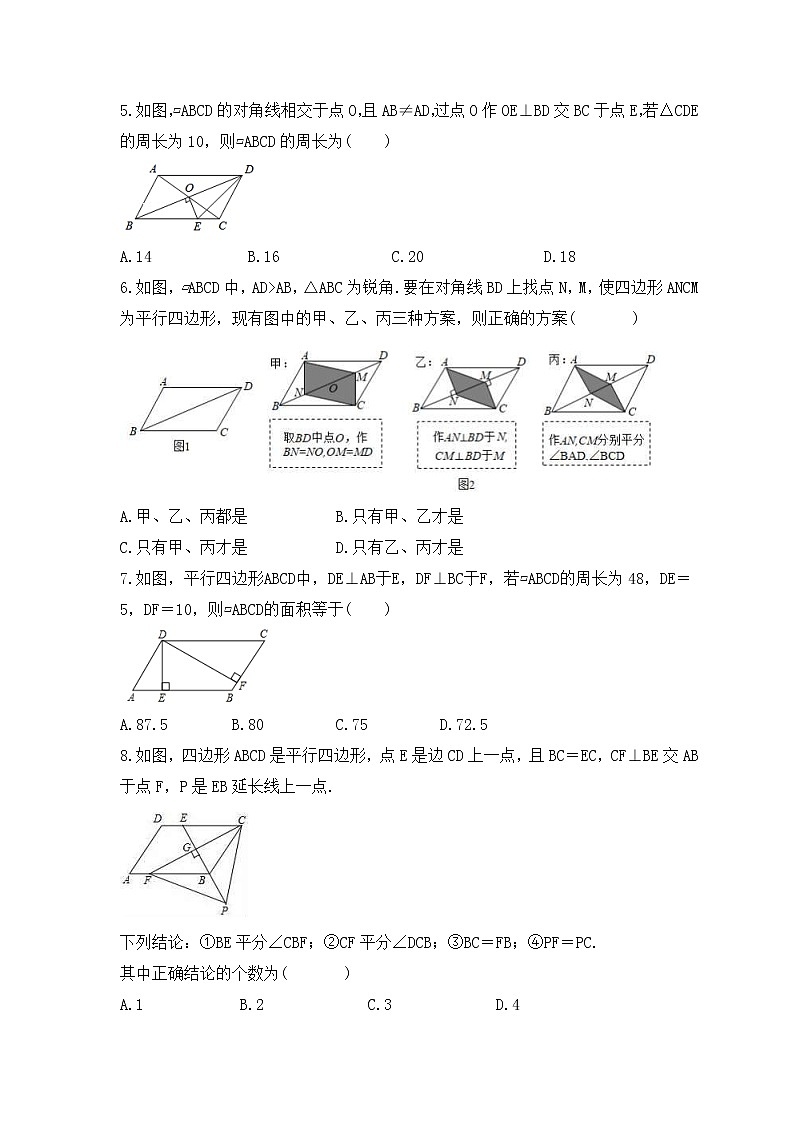
5.如图，▱ABCD的对角线相交于点O，且AB≠AD，过点O作OE⊥BD交BC于点E，若△CDE的周长为10，则▱ABCD的周长为(　　)

A.14                          B.16                            C.20                             D.18

6.如图，▱ABCD中，AD>AB，△ABC为锐角.要在对角线BD上找点N，M，使四边形ANCM为平行四边形，现有图中的甲、乙、丙三种方案，则正确的方案(    )

A.甲、乙、丙都是           B.只有甲、乙才是

C.只有甲、丙才是           D.只有乙、丙才是

7.如图，平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，若▱ABCD的周长为48，DE＝5，DF＝10，则▱ABCD的面积等于(    )

A.87.5                      B.80                       C.75                       D.72.5

8.如图，四边形ABCD是平行四边形，点E是边CD上一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点.

下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝PC.

其中正确结论的个数为(     )

A.1           B.2            C.3            D.4

二              、填空题

9.如图，在平行四边形ABCD中，BE平分∠ABC，交AD于点E，AB＝3cm，ED＝1.5cm，则平行四边形ABCD的周长是        .

10.如图，▱ABCD中，∠ADC＝119°，BE⊥DC于点E，DF⊥BC于点F，BE与DF交于点H，则∠BHF＝　   .

11.如图，▱ABCD中，AC＝8，BD＝6，AD＝a，则a的取值范围是　 　    .

12.在四边形ABCD中，BD是对角线，∠ABD＝∠CDB，要使四边形ABCD是平行四边形只须添加一个条件，这个条件可以是　　(只需写出一种情况).

13.如图，在平行四边形ABCD中，AB＝4，BC＝5，∠ABC＝60°，平行四边形ABCD的对角线AC、BD交于点O，过点O作OE⊥AD，则OE＝　　       .

14.如图，△ABC中，如果AB＝30，BC＝24，AC＝27，DN∥GM∥AB，EG∥DF∥AC，则图中阴影部分的三个三角形周长之和为________.

三              、解答题

15.如图，在平行四边形ABCD的边AB，CD上截取AF，CE，使得AF＝CE，连结EF，点M，N是线段EF上两点，且EM＝FN，连结AN，CM.

(1)求证：△AFN≌△CEM；

(2)若∠CMF＝107°，∠CEM＝72°，求∠NAF的度数．

16.如图，已知在▱ABCD中，对角线AC，BD交于点O，AB⊥AC，AB＝1，BC＝.

⑴求平行四边形ABCD的面积S▱ABCD；

⑵求对角线BD的长.

17.如图，四边形ABCD是平行四边形，对角线AC与BD交于点O，点E是BC边上一点，只用一把无刻度的直尺在AD边上作点F，使得DF＝BE.

(1)如图1，①请画出满足题意的点F，保留痕迹，不写作法；

②依据你的作图，证明：DF＝BE.

(2)如图2，若点E是BC边中点，请只用一把无刻度的直尺作线段FG，使得FG∥BD，分别交AD、AB于点F、点G.

18.如图1，在△ABC中，AB＝AC，∠ABC＝α，D是BC边上一点，以AD为边作△ADE，使AE＝AD，∠DAE＋∠BAC＝180°.

(1)直接写出∠ADE的度数(用含α的式子表示)；

(2)以AB，AE为边作平行四边形ABFE，

①如图2，若点F恰好落在DE上，求证：BD＝CD；

②如图3，若点F恰好落在BC上，求证：BD＝CF.

参考答案

1.D.

2.C

3.C.

4.C

5.C.

6.A

7.B

8.D.

9.答案为：15cm.

10.答案为：61°.

11.答案为：1＜a＜7.

12.答案为：AB＝CD或AD∥BC

13.答案为：.

14.答案为：81.

15.证明：(1)∵四边形ABCD是平行四边形，

∴CD∥AB，

∴∠AFN＝∠CEM.

∵FN＝EM，AF＝CE，

∴△AFN≌△CEM(SAS)．

(2)解：∵△AFN≌△CEM，

∴∠NAF＝∠ECM.

∵∠CMF＝∠CEM＋∠ECM，

∴107°＝72°＋∠ECM，

∴∠ECM＝35°，

∴∠NAF＝35°.

16.解:(1)在Rt△ABC中,AC＝2,

则S▱ABCD＝AB×AC＝2.

(2)∵四边形ABCD是平行四边形,

∴AO＝OC,BO＝OD,

∴AO＝1,

在Rt△ABO中,BO＝,

∴BD＝2.

17.解：(1)如图，连接EO并延长交AD于F，则点F即为所求；

(2)连接BF，

∵四边形ABCD是平行四边形，

∴AD∥BC，OD＝OB，

∴∠FDO＝∠EBO，∠DFO＝∠BEO，

在△DFO和△BEO中，

，

∴△DFO≌△BEO，

∴DF＝BE；

(3)如图2所示，线段FG就是所求的线段.

18.解：(1)∵在△ABC中，AB＝AC，∠ABC＝α，

∴∠BAC＝180°﹣2α，

∵∠DAE＋∠BAC＝180°，

∴∠DAE＝2α，

∵AE＝AD，

∴∠ADE＝90°﹣α；

(2)①证明：∵四边形ABFE是平行四边形，

∴AB∥EF.

∴∠EDC＝∠ABC＝α，

由(1)知，∠ADE＝90°﹣α，

∴∠ADC＝∠ADE＋∠EDC＝90°，

∴AD⊥BC.

∵AB＝AC，

∴BD＝CD；

②证明：∵AB＝AC，∠ABC＝α，

∴∠C＝∠B＝α.

∵四边形ABFE是平行四边形，

∴AE∥BF，AE＝BF.

∴∠EAC＝∠C＝α，