

2022-2023学年广东省佛山市七年级下册数学期中专项提升模拟(AB卷)含解析
展开2022-2023学年广东省佛山市七年级下册数学期中专项提升模拟
(A卷)
一、选一选(每小题3分,共30分)
1. 的平方根是( )
A. 3 B. ±3 C. D. ±
2. 用没有等式表示:的倍与的差是负数( ).
A. B. C. D.
3. 已知a
A. B. C. D.
5. 要下面几个问题,你认为没有应做抽样是( ).
A. 某电视剧的收视率 B. “神舟七号”飞船重要零部件的产品质量
C. 一批炮弹的伤力 D. 一片森林的树木有多少棵
6. 下列说确的是( )
A. 同位角相等
B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角
D. 在同一平面内,如果a∥b,b∥c,则a∥c
7. 如图所示,下列推理没有正确的是( )
A. 若∠1=∠C,则AE∥CD
B. 若∠2=∠BAE,则AB∥DE
C. 若∠B+∠BAD=180°,则AD∥BC
D. 若∠C+∠ADC=180°,则AE∥CD
8. 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A. 景仁宫(4,2) B. 养心殿(-2,3)
C. 保和殿(1,0) D. 武英殿(-3.5,-4)
9. 如图,小明从家到学校分别有①、②、③三条路可走:①为折线段ABCDEFG,②为折线段AIG,③为折线段AJHG.三条路的长依次为a、b、c,则( )
A. a>b>c B. a=b>c C. a>c>b D. a=b<c
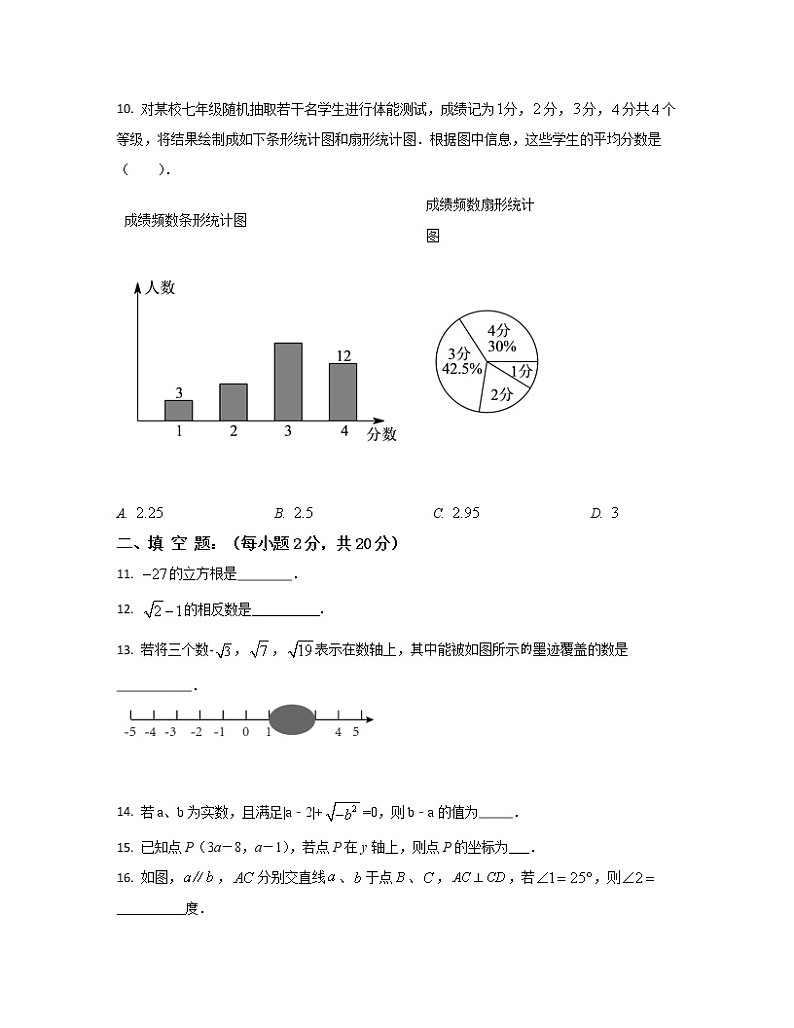
10. 对某校七年级随机抽取若干名学生进行体能测试,成绩记为分,分,分,分共个等级,将结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是( ).
成绩频数条形统计图
成绩频数扇形统计图
A. B. C. D.
二、填 空 题:(每小题2分,共20分)
11. 的立方根是________.
12. 的相反数是__________.
13. 若将三个数-,,表示在数轴上,其中能被如图所示墨迹覆盖的数是___________.
14. 若a、b为实数,且满足|a﹣2|+=0,则b﹣a的值为_____.
15. 已知点P(3a-8,a-1),若点P在y轴上,则点P的坐标为___.
16. 如图,,分别交直线、于点、,,若,则__________度.
17. 若关于的方程的解是负数,则的取值范围是__________.
18. 如果关于的没有等式组的解集为,那么的取值范围是_____________
19. 超市为了制定某个时间段收银台开放,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成频数分布直方图(图中等待时间分钟表示大于或等于分钟而小于分钟,其余类似),这个时间段内顾客等待时间低于分钟的有__________人.
20. 在平面直角坐标系中,点的坐标为,点在坐标轴上,,则点的坐标为__________.
第Ⅱ卷
三、解 答 题(共50分)
21. 计算:.
22. 解没有等式(组).
()求没有等式的正整数解.
().
23. 按要求画图:
()作交于.
()连接,作交的延长线于.
()作于.
24. 看图填空:
已知:如图,E为DF上的点,B为AC上的点,∠1 =∠2,∠C =∠D.求证:AC∥DF
证明:
∵∠1 =∠2( )
∠1 =∠3,∠2 =∠4( )
∴∠3 =∠4( )
∴_______∥_______( )
∴∠C=∠ABD( )
又∵∠C =∠D( )
∴ ∠D=∠ABD( )
∴AC∥DF( )
25. 某商场去年前五个月额共计万元.下表表示该商场去年前五个月的月额(统计信息没有全).图①表示该商场服装部各月额占商场当月额的百分比情况统计图.
商场月额统计表
单位:万元
月份
月
月
月
月
月
商场月额
服装部各月额占市场
当月额百分比统计图
月份服装部各卖区额
占月份服装部额的百分比统计图
()商场月份的额是__________万元.
()服装部月份额是__________万元.
小明同学观察图①后认为,服装部月份的额比服装部月份的额减少了,你同意他的看法吗?请说明理由.
答:__________.
()在该商场服装部,下设、、、、五个卖区,图②表示在月份,服装部各卖区额占月份服装部额的百分比情况统计图.则__________卖区的额,额的卖区占月份商场额的百分比是__________.
26. 已知:△ABC的三个顶点坐标A(﹣2,0),B(5,0),C(4,3),在平面直角坐标系中画出△ABC,并求△ABC的面积.
27. 列没有等式解应用题:在奥运知识竞赛有 道选一选,每道题的四个选项中,有且只有一个答案正确,选对得 分,没有选或错选扣 分,如果得分没有低于 分才能得奖,那么要得奖至少应答对多少道题?
28. 已知:如图,,,.求证:.
29. 在平面直角坐标系中,的三个顶点位置如图所示,点的坐标是,现将平移,使点移动到点,且点,分别是,的对应点.
()请画出平移后的(没有写画法).
并直接写出点,的坐标:( ),( ).
()若三角形内部有一点,则对应点的坐标是( ).
()如果坐标平面内有一点,使得以,,,为顶点的四边形为平行四边形,请直接写出点的坐标.
四、附加题(本大题共20分,第30小题6分,第31、32小题各7分)
30. 如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向依次没有断地移动,每次移动一个单位,得到点,,,,则点的坐标为__________,点的坐标为__________,点(是自然数)的坐标为__________.
31. 作图题(没有写作法)
()如图,一个牧童从点出发,赶着羊群去河边喝水,则应当怎样选择饮水路线,才能使羊群走的路程最短?请在图中画出最短路线.
()如图,直线是一条河,,是两个村庄,欲在上的某处修建一个水泵站,向,两地供水,要使所需管道的长度最短,在图中标出点.(保留作图过程)
()如图,在一条河的两岸有,两个村庄,现在要在河上建一座小桥,桥的方向与河岸方向垂直,桥在图中用一条线段表示.试问:桥建在何处,才能使到的路程最短呢?请在图中画出桥的位置.(保留作图过程)
32. 某工厂有甲种原料千克,乙种原料千克,现计划用这两种原料生产,两种型号的产品用件.已知每件型号产品需要甲种原料千克,乙种原料千克;每件型号产品需要甲种原料千克,乙种原料千克.请解答下列问题:
()该工厂有哪几种生产?
()在这批产品全部售出的条件下,若件型号产品获利元,件型号产品获利元,()中哪种获利?利润是多少?
2022-2023学年广东省佛山市七年级下册数学期中专项提升模拟
(A卷)
一、选一选(每小题3分,共30分)
1. 的平方根是( )
A. 3 B. ±3 C. D. ±
【正确答案】D
【分析】先计算的值为3,再利用平方根的定义即可得到结果.
【详解】解:∵=3,
∴的平方根是±.
故选:D.
此题考查了平方根,以及算术平方根,解决本题的关键是先求得的值.
2. 用没有等式表示:的倍与的差是负数( ).
A. B. C. D.
【正确答案】B
【详解】x的2倍表示为:2x,
与4的差表示为2x−4,
由题意得:2x−4<0,
故选B.
3. 已知a
【分析】根据没有等式的性质即可判断.
【详解】∵a
此题主要考查没有等式,解题的关键是熟知没有等式的性质.
4. 下列四个数中,无理数是( ).
A. B. C. D.
【正确答案】C
【详解】A. 是无限循环小数是有理数,故本选项错误;
B. 是无理数,故本选项错误;
C. 是无理数,故本选项正确;
D. =-3,是有理数,故本选项错误;故选C.
5. 要下面几个问题,你认为没有应做抽样的是( ).
A. 某电视剧的收视率 B. “神舟七号”飞船重要零部件的产品质量
C. 一批炮弹的伤力 D. 一片森林的树木有多少棵
【正确答案】C
【详解】A.某电视剧的收视率,的范围较大,故可使用抽样的方式;
B. “神舟七号”飞船重要零部件的产品质量,的范围较小,故可使用普查的方式;
C.一批炮弹的伤力,具有一定的破坏性,故可使用抽样的方式;
D. 一片森林的树木有多少棵,的范围较大,故可使用抽样的方式.
故选C.
6. 下列说确的是( )
A. 同位角相等
B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角
D. 在同一平面内,如果a∥b,b∥c,则a∥c
【正确答案】D
【分析】根据同位角的定义、垂线的性质、对顶角的性质、平行公理依次判断.
【详解】解:A. 同位角没有一定相等,故该项没有符合题意;
B. 在同一平面内,如果a⊥b,b⊥c,则a//c,故该项没有符合题意;
C. 相等的角没有一定是对顶角,故该项没有符合题意;
D. 在同一平面内,如果a//b,b//c,则a//c,故该项符合题意;
故选:D.
此题考查了语句的判断,正确掌握同位角的定义、垂线的性质、对顶角的性质、平行公理是解题的关键.
7. 如图所示,下列推理没有正确的是( )
A. 若∠1=∠C,则AE∥CD
B. 若∠2=∠BAE,则AB∥DE
C. 若∠B+∠BAD=180°,则AD∥BC
D. 若∠C+∠ADC=180°,则AE∥CD
【正确答案】D
【详解】A. ∵∠1=∠C,∴AE ∥ CD( 同位角相等 , 两直线平行 ) ,故正确;
B. ∵∠2=∠BAE,∴AB ∥ DE( 内错角相等 , 两直线平行 ) ,故正确;
C. ∵∠B+∠BAD=180∘,∴AD ∥ BC( 同旁内角互补 , 两直线平行 ) ,故正确;
D. ∵∠C+∠ADC=180∘,∴AD ∥ BC( 同旁内角互补 , 两直线平行 ) ,故错误.
故选D.
8. 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A. 景仁宫(4,2) B. 养心殿(-2,3)
C 保和殿(1,0) D. 武英殿(-3.5,-4)
【正确答案】B
【详解】试题分析:本题考查了点的坐标问题,解题关键是找出原点的位置,然后根据平面直角坐标系的特点找出各个选项的正确坐标,即根据太和门的点的坐标为(0,-1),可得中和殿为原点(0,0),保和殿为(0,1),景仁宫(2,4),养心殿(-2,3),武英殿(-3.5,-3),所以只有B正确,故选B.
考点:点的坐标
9. 如图,小明从家到学校分别有①、②、③三条路可走:①为折线段ABCDEFG,②为折线段AIG,③为折线段AJHG.三条路的长依次为a、b、c,则( )
A. a>b>c B. a=b>c C. a>c>b D. a=b<c
【正确答案】B
【详解】观察图形,可知:①②相等,③最短,
a、b、c的大小关系是:a=b>c.故选B.
本题考查线段长短的度量、比较, 根据平移的性质,两点间线段距离最短,认真观察图形,可知①②都是相当于走直角线,故①②相等,③走的是两点间的线段,最短.
10. 对某校七年级随机抽取若干名学生进行体能测试,成绩记为分,分,分,分共个等级,将结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是( ).
成绩频数条形统计图
成绩频数扇形统计图
A. B. C. D.
【正确答案】C
【详解】由题意得总人数为:(人),所以分等级的人数为:(人),2分等级的人数为:40-17-3-12=8(人),故平均分为:(分).
故本题正确答案为C.
二、填 空 题:(每小题2分,共20分)
11. 的立方根是________.
【正确答案】-3
【分析】根据立方根的定义求解即可.
【详解】解:-27的立方根是-3,
故-3.
本题考查了立方根的定义,属于基础题型,熟知立方根的概念是解题的关键.
12. 的相反数是__________.
【正确答案】
【分析】根据相反数的定义直接可得出答案
【详解】解:因-(﹣1)= 1﹣.
所以﹣1相反数是1﹣.
故1﹣
13. 若将三个数-,,表示在数轴上,其中能被如图所示的墨迹覆盖的数是___________.
【正确答案】
【分析】利用无理数的估算,估算出-,,的范围,即可确定墨迹覆盖的数.
【详解】∵-2<-<-1,2<<3,3<<4,且墨迹覆盖的范围是1-3,
∴能被墨迹覆盖的数是.
故答案是:.
本题主要考查的是无理数的估算,掌握估算方法是解题的关键.
14. 若a、b为实数,且满足|a﹣2|+=0,则b﹣a的值为_____.
【正确答案】-2
【详解】解:由题意得,a−2=0,−b²=0,
解得a=2,b=0,
所以,b−a=0−2=−2.
故答案为−2.
15. 已知点P(3a-8,a-1),若点P在y轴上,则点P的坐标为___.
【正确答案】
【分析】先根据y轴上的点的坐标的特征求得a的值,即可求得点P的坐标.
【详解】由题意得,解得,
则,
所以点P的坐标为,
故.
本题考查坐标轴上的点的坐标,解题的关键是熟练掌握坐标轴上的点的坐标的特征:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.
16. 如图,,分别交直线、于点、,,若,则__________度.
【正确答案】65
【详解】解:如图:
∵,
∴,
∵,
∴,
∵,
∴.
故答案为65
本题考查了平行线的性质,垂直的定义,是基础题,熟记性质是解题的关键.
17. 若关于的方程的解是负数,则的取值范围是__________.
【正确答案】a<3
【详解】解这个关于x的方程,得
x=a-3
根据方程的解是负数可知
a-3<0
解这个没有等式,得
a<3故答案为a<3.
点睛:本题考查了一元没有等式的解法的知识点,只要是掌握和熟练运用一元没有等式的解题方法这些知识点进行解题,即可得出答案.
18. 如果关于的没有等式组的解集为,那么的取值范围是_____________
【正确答案】a⩽3
【分析】根据“同大取大”即可得到a的取值范围;
【详解】∵关于x的没有等式组的解集为x>3,
∴3⩾a,
∴a⩽3,
故答案为a⩽3.
此题考查没有等式的解集,解题关键在于掌握其性质.
19. 超市为了制定某个时间段收银台开放,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成频数分布直方图(图中等待时间分钟表示大于或等于分钟而小于分钟,其余类似),这个时间段内顾客等待时间低于分钟的有__________人.
【正确答案】60
【详解】根据频数分布直方图得到前3组的等待时间没有少于3分钟,而它们的频数分别为10,35,15,
所以这个时间段内顾客等待时间低于3分钟的人数为(人).
故答案为60.
20. 在平面直角坐标系中,点的坐标为,点在坐标轴上,,则点的坐标为__________.
【正确答案】或或或
【详解】(1)当点B在x轴上时,
∵,
∴,
∵,
∴,
∴,
∴或.
(2)当点B在y轴上时,
∵,
∴,
∵,
∴,
∴,
∴或.故答案为或 ,或.
第Ⅱ卷
三、解 答 题(共50分)
21. 计算:.
【正确答案】
【详解】分析:分别进行二次根式的化简、三次根式的化简,继而合并可得出答案.
本题解析:.
22. 解没有等式(组).
()求没有等式的正整数解.
().
【正确答案】(),,,().
【详解】分析:(1)先求出没有等式的解集,然后根据它的解集求其正整数解.
(2)先求出没有等式组中每一个没有等式的解集,再求出它们的公共部分,则两个没有等式的解集的公共部分就是没有等式组的解集.
本题解析:
(),
,
,
,
,
.
所以正整数解:,,,.
()解:①得,
,
解②得,
,
,
∴.
点睛:本题考查了一元没有等式组的解法,关键是解一元没有等式,解一元没有等式的方法与解一元方程的方法基本相同,没有同点是系数化成1时,要注意没有等号方向的变化.
23. 按要求画图:
()作交于.
()连接,作交的延长线于.
()作于.
【正确答案】作图见解析
【详解】试题分析:(1)过点B作∠BEC=∠D即可得出答案;
(2)延长DC,作∠BFC=∠ACD即可得出答案;
(3)过点A作AG⊥CD,直接作出垂线即可.
试题解析:(1)如图所示:BE即为所求;
(2)如图所示:BF即为所求;
(3)如图所示:AG即为所求.
点睛:此题主要考查了基本作图,正确根据要求作出图形是作图的基本能力.
24. 看图填空:
已知:如图,E为DF上的点,B为AC上的点,∠1 =∠2,∠C =∠D.求证:AC∥DF
证明:
∵∠1 =∠2( )
∠1 =∠3,∠2 =∠4( )
∴∠3 =∠4( )
∴_______∥_______( )
∴∠C=∠ABD( )
又∵∠C =∠D( )
∴ ∠D=∠ABD( )
∴AC∥DF( )
【正确答案】已知;对顶角相等;等量代换;DB;EC;内错角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行
【分析】根据平行线的判定与性质,上下文求解即可.
【详解】∵∠1 =∠2(已知)
∠1=∠3,∠2=∠4(对顶角相等)
∴∠3=∠4(等量代换)
∴BD∥CE(内错角相等,两直线平行)
∴∠C=∠ABD(两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF(内错角相等,两直线平行)
故已知;对顶角相等;等量代换;BD;CE;内错角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行
此题考查了平行线的判定与性质,掌握平行线的判定与性质是解题的关键.
25. 某商场去年前五个月额共计万元.下表表示该商场去年前五个月的月额(统计信息没有全).图①表示该商场服装部各月额占商场当月额的百分比情况统计图.
商场月额统计表
单位:万元
月份
月
月
月
月
月
商场月额
服装部各月额占市场
当月额的百分比统计图
月份服装部各卖区额
占月份服装部额的百分比统计图
()商场月份的额是__________万元.
()服装部月份的额是__________万元.
小明同学观察图①后认为,服装部月份的额比服装部月份的额减少了,你同意他的看法吗?请说明理由.
答:__________.
()在该商场服装部,下设、、、、五个卖区,图②表示在月份,服装部各卖区额占月份服装部额的百分比情况统计图.则__________卖区的额,额的卖区占月份商场额的百分比是__________.
【正确答案】(1)120(2)小明说法错误(3)28%
【详解】分析:(1)由总额减去其他月份的额求出5月的额即可;
(2)用5月份的总额乘以30%即可得到结果;(3)观察图②可知B卖区额,B卖区额÷5月的额即可求解.
本题解析:
()(万元).
()(万元).
月和月额分别是万元和万元,
服装额各点当月的和,则月为(万元),
月为万元,故小明说法错误.
()卖区,卖区的额占商场月份额的百分比是百分之二十八.
点睛:本题是统计题,考查了条形统计图和折线统计图,是基础知识要熟练掌握.本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从没有同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据
26. 已知:△ABC的三个顶点坐标A(﹣2,0),B(5,0),C(4,3),在平面直角坐标系中画出△ABC,并求△ABC的面积.
【正确答案】
【分析】利用三角形的面积计算即可.
【详解】解:.
27. 列没有等式解应用题:在奥运知识竞赛有 道选一选,每道题的四个选项中,有且只有一个答案正确,选对得 分,没有选或错选扣 分,如果得分没有低于 分才能得奖,那么要得奖至少应答对多少道题?
【正确答案】至少应答对道题
【详解】分析:设得奖者选对x道题,则没有选或选错(25-x)道题,根据得分没有低于60分得奖,可得出没有等式,解出即可.
本题解析:
设做对道,则做错或没有做有道,
列式,
解得,
,
.
∵为整数,
∴至少应选对道题.
答:至少应答对道题.
点睛:本题主要考查了一元没有等式的应用,解决本题的关键是弄清题意,表示出做对题目的得分,做错题目的扣分,然后列出没有等式.
28. 已知:如图,,,.求证:.
【正确答案】证明见解析
【详解】分析:先根据平行线的判定证明EF∥AD,再由垂直的定义即可得证.
本题解析:
∵,
∴,
∵,
∴,
∴,
∵,
∴.
29. 在平面直角坐标系中,的三个顶点位置如图所示,点的坐标是,现将平移,使点移动到点,且点,分别是,的对应点.
()请画出平移后的(没有写画法).
并直接写出点,的坐标:( ),( ).
()若三角形内部有一点,则的对应点的坐标是( ).
()如果坐标平面内有一点,使得以,,,为顶点的四边形为平行四边形,请直接写出点的坐标.
【正确答案】答案见解析
【详解】分析:(1)根据网格结构找出点B、C平移后的位置,然后顺次连接即可,根据平面直角坐标系写出点B′、C′的坐标即可;(2)根据平移规律写出即可.(3)根据平面直角坐标系写出D点坐标即可.
本题解析:
()已知点坐标,是,
所以判断到是向左移个单位,
向下移个单位.
所以∵,,
∴,.
()由()问知.
()①∵四边形,知向,
向上移位,向左移位,
∴向,上移位,左移位得.
②∵四边形知向,
向下移位,向右移位,
∴向下移位,右移位得.
③∵四边形,知向下移位,右移位,
∴向下移位,右移位得.
四、附加题(本大题共20分,第30小题6分,第31、32小题各7分)
30. 如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向依次没有断地移动,每次移动一个单位,得到点,,,,则点的坐标为__________,点的坐标为__________,点(是自然数)的坐标为__________.
【正确答案】 ①. ②. ③.
【详解】分析:根据图象可得移动4次完成一个循环,且相邻两个周期中对应点的横坐标相差2、纵坐标相同;由上述提示可知A4n+1与A1相对应,横坐标相差n个2、纵坐标相同,再点A1的坐标,即可得到点A4n+1的坐标.
本题解析:根据动点的移动规律可知,移动4次完成一个循环,且相邻两个周期中对应点的横坐标相差2、纵坐标相同,
∴A4n+1与A1相对应,横坐标相差n个2、纵坐标相同,
∴,,
故A4n+1的坐标为(2n,1)(n是自然数).
故答案为 (1). (2). (3). .
31. 作图题(没有写作法)
()如图,一个牧童从点出发,赶着羊群去河边喝水,则应当怎样选择饮水路线,才能使羊群走的路程最短?请在图中画出最短路线.
()如图,直线是一条河,,是两个村庄,欲在上的某处修建一个水泵站,向,两地供水,要使所需管道的长度最短,在图中标出点.(保留作图过程)
()如图,在一条河的两岸有,两个村庄,现在要在河上建一座小桥,桥的方向与河岸方向垂直,桥在图中用一条线段表示.试问:桥建在何处,才能使到的路程最短呢?请在图中画出桥的位置.(保留作图过程)
【正确答案】作图见解析
【详解】分析:(1)把河岸看做一条直线,利用点到直线的所有连接线段中,垂直线段最短的性质即可解决问题.(2)根据两点之间线段最短解答.(3)先确定AA′=CD,且AA′∥CD,连接BA′,与河岸的交点就是点C,过点C作CD垂直河岸,交另一河岸于点D,CD就是所求的桥的位置.
本题解析:
()如图
点到直线垂线段最短.
()如图.
()
32. 某工厂有甲种原料千克,乙种原料千克,现计划用这两种原料生产,两种型号的产品用件.已知每件型号产品需要甲种原料千克,乙种原料千克;每件型号产品需要甲种原料千克,乙种原料千克.请解答下列问题:
()该工厂有哪几种生产?
()在这批产品全部售出的条件下,若件型号产品获利元,件型号产品获利元,()中哪种获利?利润是多少?
【正确答案】(1)3种(2)2400
【详解】分析:(1)设生产A型号产品x件,则生产B型号产品(80-x)件,根据原材料的数量与每件产品的用量建立没有等式组,求出其解即可;(2)设所获利润为W元,根据总利润=A型号产品的利润+B型号产品的利润建立W与x之间的函数关系式,求出其解即可;
本题解析:
()设种产品生产件,种产品生产件,
由题意可列没有等式组:,
解得,
所以工厂可以有种.
①生产型号产品件,生产型产品件;
②生产型号产品件,生产型产品件;
③生产型号产品件,生产型产品件.
()因为产品获利较高,所以当时获利为
(元).
点睛:本题考查了列一元没有等式组解实际问题运用,一元没有等式组的解法的运用,解本题的关键是读懂题意,找到符合题意的没有等关系式组,及所求量的等量关系.
2022-2023学年广东省佛山市七年级下册数学期中专项提升模拟
(B卷)
一.选一选(每小题 3 分,共 30 分)
1. 计算正确是( )
A. (﹣5)0=0 B. x3+x4=x7 C. (﹣a2b3)2=﹣a4b6 D. 2a2•a﹣1=2a
2. 如图,,,点,,在同一直线上,则的度数为
A. B. C. D.
3. 下列多项式乘法中可以用平方差公式计算是( )
A. (﹣a+b)(a﹣b) B. (x+2)(2+x) C. (+y)(y﹣) D. (x﹣2)(x+1)
4. 下列四个图形中,没有能推出∠2与∠1相等的是( )
A. B.
C. D.
5. 若 a2﹣b2=,a+b=,则 a﹣b 的值为( )
A. ﹣ B. C. 1 D. 2
6. 周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
A. 小丽在便利店时间为15分钟
B. 公园离小丽家的距离为2000米
C. 小丽从家到达公园共用时间20分钟
D. 小丽从家到便利店的平均速度为100米/分钟
7. 如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果∠1=30°,那么∠2的度数为( )
A. 30° B. 40° C. 50° D. 60°
8. 若 a=20170,b=2015×2017﹣20162,c=(﹣)2016×()2017,则下列 a,b,c 的大小关系正确的是( )
A. a<b<c B. a<c<b C. b<a<c D. c<b<a
9. 小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
A. B. C. D.
10. 如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A. 110° B. 120° C. 125° D. 135°
二.填 空 题(每小题 4 分,共 24 分)
11. 圆面积 S 与半径 r 之间的关系式 S=πr2 中自变量是____,因变量是____,常量是____.
12. 若 5n=2,4n=3,则 20n=_.
13. 如图,BC⊥AC,BC=8,AC=6,AB=10,则点 C 到线段 AB 的距离是_____.
14. 若 25x2+kxy+4y2 是一个完全平方式,则 k=_____.
15. 已知一个长方形的长为 5cm,宽为 xcm,周长为 ycm,则 y 与 x 之间的函数表达式为_________.
16. 如图,要使AD//BF,则需要添加的条件是_____________(写一个即可).
三.解 答 题(共 66 分)
17. 如图,以点 B 顶点,射线 BC 为一边,利用尺规作∠EBC,使得∠EBC=∠A.
18. 为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).
19. 计算:
(1)(3.14﹣π)0+0.254×44﹣( )﹣1 ;
(2)﹣(a2b)3+2a2b•(﹣3a2b)2
20. 先化简,再求值:[(x﹣2y)2﹣2y(2y﹣x)]÷2x,其中 x=2,y=1.
21. 已知AB⊥BC,∠1+∠2=90°,∠2=∠3.求证:BE//DF
证明:∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,且∠2=∠3,
∴ = .理由: .
∴BE∥DF.理由是: .
22. 观察下列关于自然数的等式:
(1)32﹣4×12=5 ①
(2)52﹣4×22=9 ②
(3)72﹣4×32=13 ③
… 根据上述规律解决下列问题:
(1)完成第五个等式:112﹣4× ______2= ;
(2)写出你猜想的第 n 个等式(用含 n 的式子表示),并验证其正确性.
23. 如图:已知直线AB、CD相交于点O,∠COE=90°
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE度数.
24. 已知直线l1∥l2,l3和11,l2分别交于C,D两点,点A,B分别在线l1,l2上,且位于l3的左侧,点P在直线l3上,且没有和点C,D重合.
(1)如图1,有一动点P在线段CD之间运动时,试确定∠1、∠2、∠3之间的关系,并给出证明.
(2)如图2,当动点P在射线DC上运动时,上述的结论是否成立?若没有成立,请写出∠1、∠2、∠3的关系并证明.
2022-2023学年广东省佛山市七年级下册数学期中专项提升模拟
(B卷)
一.选一选(每小题 3 分,共 30 分)
1. 计算正确的是( )
A. (﹣5)0=0 B. x3+x4=x7 C. (﹣a2b3)2=﹣a4b6 D. 2a2•a﹣1=2a
【正确答案】D
【详解】解:A.原式=1,故A错误;
B.x3与x4没有是同类项,没有能进行合并,故B错误;
C.原式=a4b6,故C错误;
D.正确.
故选D.
2. 如图,,,点,,在同一直线上,则的度数为
A. B. C. D.
【正确答案】C
【详解】解:∵=, ∠1 =15
∴∠BOC=75
又 ∵B、O、D在同一直线上,即∠BOD=
∴∠2=∠BOD-∠BOC=180-75=105°
故选C
3. 下列多项式乘法中可以用平方差公式计算的是( )
A. (﹣a+b)(a﹣b) B. (x+2)(2+x) C. (+y)(y﹣) D. (x﹣2)(x+1)
【正确答案】C
【详解】解:根据平方差公式和完全平方公式的特点,选项A和B都是完全平方式,
选项C、.所以C平方差公式,
故选:C
4. 下列四个图形中,没有能推出∠2与∠1相等的是( )
A. B.
C. D.
【正确答案】B
【分析】根据平行线的性质以及对顶角相等的性质进行判断.
【详解】解:A、∵∠1和∠2互对顶角,
∴∠1=∠2,故本选项错误;
B、∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
没有能判断∠1=∠2,故本选项正确;
C、∵a//b,
∴∠1=∠2(两直线平行,内错角相等),故本选项错误;
D、如图,
∵a∥b,
∴∠1=∠3(两直线平行,同位角相等),
∵∠2=∠3(对顶角相等),
∴∠1=∠2,故本选项错误;
故选B.
本题考查了平行线的性质,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
5. 若 a2﹣b2=,a+b=,则 a﹣b 的值为( )
A. ﹣ B. C. 1 D. 2
【正确答案】B
【详解】∵,,
∴由a2−b2=(a+b)(a−b)得到:=(a-b),
∴a-b=.
故选B.
6. 周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
A. 小丽在便利店时间为15分钟
B. 公园离小丽家的距离为2000米
C. 小丽从家到达公园共用时间20分钟
D. 小丽从家到便利店的平均速度为100米/分钟
【正确答案】A
【分析】根据题意和函数图象可以判断各个选项是否正确.
【详解】小丽在便利店时间为15-10=5(分钟),故选项A错误,
公园离小丽家的距离为2000米,故选项B正确,
小丽从家到达公园共用时间20分钟,故选项C正确,
小丽从家到便利店的平均速度为:2000÷20=100米/分钟,故选项D正确,
故选:A.
此题考查函数的图象,解题的关键是明确题意,利用数形的思想解答.
7. 如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果∠1=30°,那么∠2的度数为( )
A. 30° B. 40° C. 50° D. 60°
【正确答案】D
【详解】如图,因∠1=30°,∠1+∠3=60°,
所以∠3=30°,
因为AD//BC,
所以∠3=∠4,
所以∠4=30°,
所以∠2=180°-90°-30°=60°,
故选:D.
8. 若 a=20170,b=2015×2017﹣20162,c=(﹣)2016×()2017,则下列 a,b,c 的大小关系正确的是( )
A. a<b<c B. a<c<b C. b<a<c D. c<b<a
【正确答案】C
【详解】解:a=20170=1,b=2015×2017﹣20162=(2016﹣1)(2016+1)﹣20162=20162﹣1-20162=﹣1,c=(﹣)2016×()2017=(﹣×)2016×=,则b<a<c.故选C.
点睛:本题考查了平方差公式,幂的乘方与积的乘方,以及零指数幂,熟练掌握运算法则及公式是解答本题的关键.
9. 小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
A. B. C. D.
【正确答案】C
【详解】小明从家到学校,先匀速步行到车站,因此S随时间t的增长而增长,
等了几分钟后坐上了公交车,因此时间在增加,S没有增长,
坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,因此S又随时间t的增长而增长,
故选:C.
10. 如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A. 110° B. 120° C. 125° D. 135°
【正确答案】D
【详解】如图所示,过E作EG∥AB.∵AB∥CD,∴EG∥CD,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠BED+∠CDE=360°.
又∵DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,
∴∠FBE+∠FDE=(∠ABE+∠CDE)=(360°﹣90°)=135°,
∴∠BFD=360°﹣∠FBE﹣∠FDE﹣∠BED=360°﹣135°﹣90°=135°.
故选D.
本题主要考查了平行线性质以及角平分线的定义的运用,解题时注意:两直线平行,同旁内角互补.解决问题的关键是作平行线.
二.填 空 题(每小题 4 分,共 24 分)
11. 圆面积 S 与半径 r 之间的关系式 S=πr2 中自变量是____,因变量是____,常量是____.
【正确答案】 ①. r ②. S ③. π
【详解】解:S=πr2中,自变量为:r,因变量为:S,常量为:π.故答案为r,s,π.
12. 若 5n=2,4n=3,则 20n=_.
【正确答案】6
【详解】解:.故答案为6.
13. 如图,BC⊥AC,BC=8,AC=6,AB=10,则点 C 到线段 AB 的距离是_____.
【正确答案】4.8
【详解】如图,过点C作CD⊥AB于点D,
∵BC⊥AC,
∴S△ABC=AC·BC=AB·CD,
又∵AC=6,BC=8,AB=10,
∴CD,解得:CD=4.8,
即点C到AB的距离为4.8.
点睛:(1)点C到AB的距离是点C到AB的垂线段的长度;(2)作出CD⊥AB于点D,即可利用“直角三角形的面积既等于两直角边乘积的一半,也对应斜边与斜边上高的乘积的一半”求得CD的长.
14. 若 25x2+kxy+4y2 是一个完全平方式,则 k=_____.
【正确答案】±20
【详解】解:中间一项为加上或减去5x和2y积的2倍.故k=±20.故答案为±20.
点睛:本题是完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
15. 已知一个长方形的长为 5cm,宽为 xcm,周长为 ycm,则 y 与 x 之间的函数表达式为_________.
【正确答案】y=2x+10
【分析】根据长方形的周长公式列出算式即可.
【详解】一个长方形的长为5cm,宽为 xcm,周长为ycm,则y与x之间的函数表达式为y=2x+10.
故答案为y=2x+10.
本题考查了根据实际问题列函数关系式,用到的知识点是长方形的周长公式.
16. 如图,要使AD//BF,则需要添加的条件是_____________(写一个即可).
【正确答案】∠A+∠ABC=180°或∠D+∠DCB=180°或∠A=∠EBF或D∠=∠DCF(任意写一个即可,没有必写全)
【分析】根据同位角相等,两直线平行或同旁内角互补,两直线平行,或内错角相等,两直线平行添加条件即可.
【详解】当∠ADC=∠DCF时,由内错角相等两直线平行可以得出AD//BF;
故答案为∠ADC=∠DCF.
本题考查了平行线的判定,熟练掌握平行线的判定定理容易解出本题.
三.解 答 题(共 66 分)
17. 如图,以点 B 为顶点,射线 BC 为一边,利用尺规作∠EBC,使得∠EBC=∠A.
【正确答案】答案见解析
【分析】分两种情况:①当所作的角在∠DAC内时,②当所作的角在BC下方时,首先以A为圆心,任意长为半径画弧,交AD、AC于M、F,再以B为圆心,AM长为半径画弧,交BC于N,再以N为圆心,MF长为半径画弧,交前弧与H,过H作射线BE可得∠EBC=∠A.
【详解】解:如图所示:
①当所作的角在∠DAC内时:
②当所作的角在BC下方时:
本题主要考查了基本作图,关键是掌握作一个角等于已知角的方法,注意要分类讨论,没有要漏解.
18. 为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).
【正确答案】(1)t,Q;(2)100,6;(3)
【详解】试题分析:(1)根据变量的定义即可判断.
(2)当t=0时,此时油箱剩余油量即为油箱大小,根据表格可知,1小时共耗油6升.
(3)根据(2)即可求出Q的关系式.
试题解析:解:(1)t;Q.
(2)100;6.
(3)由(2)可知:Q=100﹣6t.
19. 计算:
(1)(3.14﹣π)0+0.254×44﹣( )﹣1 ;
(2)﹣(a2b)3+2a2b•(﹣3a2b)2
【正确答案】(1)0;(2)
【详解】试题分析:(1)原式利用零指数幂法则、积的乘方,负整数指数幂法则计算即可得到结果;
(2)原式利用幂的乘方运算法则,以及单项式乘以单项式法则计算,即可得到结果.
试题解析:解:(1)原式==1+1-2=0;
(2)原式===.
20. 先化简,再求值:[(x﹣2y)2﹣2y(2y﹣x)]÷2x,其中 x=2,y=1.
【正确答案】 ;0
【详解】试题分析:根据完全平方公式、单项式乘多项式、多项式除以单项式可以化简题目中的式子,然后将x、y的值代入化简的式子即可解答本题.
试题解析:解:原式=[x2﹣4xy+4y2﹣4y2+2xy]÷2x
=(x2﹣2xy)÷2x
=
当x=2,y=1时,原式==0.
点睛:本题考查了整式的混合运算﹣化简求值,解答本题的关键是明确整式的化简求值的计算方法.
21. 已知AB⊥BC,∠1+∠2=90°,∠2=∠3.求证:BE//DF
证明:∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,且∠2=∠3,
∴ = .理由是: .
∴BE∥DF.理由是: .
【正确答案】见解析
【详解】试题分析:根据等角的余角相等,得到根据同位角相等,两直线平行,即可判定.
试题解析:BE∥DF,
即
又
且
理由是:等角的余角相等,
∴BE∥DF,
理由是:同位角相等,两直线平行.
故答案为90;90;∠1,∠4;等角的余角相等;同位角相等,两直线平行.
22. 观察下列关于自然数的等式:
(1)32﹣4×12=5 ①
(2)52﹣4×22=9 ②
(3)72﹣4×32=13 ③
… 根据上述规律解决下列问题:
(1)完成第五个等式:112﹣4× ______2= ;
(2)写出你猜想的第 n 个等式(用含 n 的式子表示),并验证其正确性.
【正确答案】(1)5,21;(2),证明见解析
【详解】试题分析:(1)根据前三个找出规律,写出第五个等式;
(2)用字母表示变化规律,根据完全平方公式计算,即可证明.
试题解析:解:(1)112﹣4×52=21.故答案为5;21;
(2)第n个等式为:(2n+1)2﹣4n2=4n+1.证明如下:
(2n+1)2﹣4n2=4n2+4n+1﹣4n2=4n+1.
点睛:本题考查的是整式的混合运算、数字的变化,掌握整式的混合运算法则、正确找出数字的变化规律是解题的关键.
23. 如图:已知直线AB、CD相交于点O,∠COE=90°
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数.
【正确答案】(1)54°;(2)120°
【详解】试题分析:(1)根据平角的定义求解即可;
(2)根据平角的定义可求∠BOD,根据对顶角的定义可求∠AOC,根据角的和差关系可求∠AOE的度数.
试题解析:解:(1)∵∠AOC=36°,∠COE=90°,∴∠BOE=180°﹣∠AOC﹣∠COE=54°;
(2)∵∠BOD:∠BOC=1:5,∴∠BOD=180°×=30°,∴∠AOC=30°,∴∠AOE=30°+90°=120°.
24. 已知直线l1∥l2,l3和11,l2分别交于C,D两点,点A,B分别在线l1,l2上,且位于l3的左侧,点P在直线l3上,且没有和点C,D重合.
(1)如图1,有一动点P在线段CD之间运动时,试确定∠1、∠2、∠3之间的关系,并给出证明.
(2)如图2,当动点P在射线DC上运动时,上述的结论是否成立?若没有成立,请写出∠1、∠2、∠3的关系并证明.
【正确答案】(1)∠2=∠1+∠3;(2)没有成立,应为∠3=∠1+∠2,证明见解析.
【详解】试题分析:(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,故可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)设PB与l1交于点F,根据l1∥l2可知∠3=∠PFC.在△APF中,根据∠PFC是△APF的一个外角即可得出结论.
试题解析:解:(1)∠2=∠1+∠3.证明如下:
如图①,过点P作PE∥l1.∵l1∥l2,∴PE∥l2,∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,∴∠2=∠1+∠3;
(2)上述结论没有成立,新的结论:∠3=∠1+∠2.证明如下:
如图②,设PB与l1交于点F.∵l1∥l2,∴∠3=∠PFC.
在△APF中,∵∠PFC是△APF的一个外角,∴∠PFC=∠1+∠2,即∠3=∠1+∠2.
点睛:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
2022-2023学年广东省深圳市七年级下册数学期中专项提升模拟(AB卷)含解析: 这是一份2022-2023学年广东省深圳市七年级下册数学期中专项提升模拟(AB卷)含解析,共39页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年上海市浦东新区七年级下册数学期中专项提升模拟(AB卷)含解析: 这是一份2022-2023学年上海市浦东新区七年级下册数学期中专项提升模拟(AB卷)含解析,共38页。试卷主要包含了选一选,填 空 题,简答题,解 答 题等内容,欢迎下载使用。
2022-2023学年福建省区域七年级下册数学期中专项提升模拟(AB卷)含解析: 这是一份2022-2023学年福建省区域七年级下册数学期中专项提升模拟(AB卷)含解析,共39页。试卷主要包含了选一选.,填 空 题.,解 答 题等内容,欢迎下载使用。












