2023年河北省中考数学复习全方位第25讲 点与圆直线与圆的位置关系 课件

这是一份2023年河北省中考数学复习全方位第25讲 点与圆直线与圆的位置关系 课件，共57页。PPT课件主要包含了真题演练，3x≥18，考点梳理，点在圆上，点在圆内，点在圆外，d＜r，题型突破等内容，欢迎下载使用。

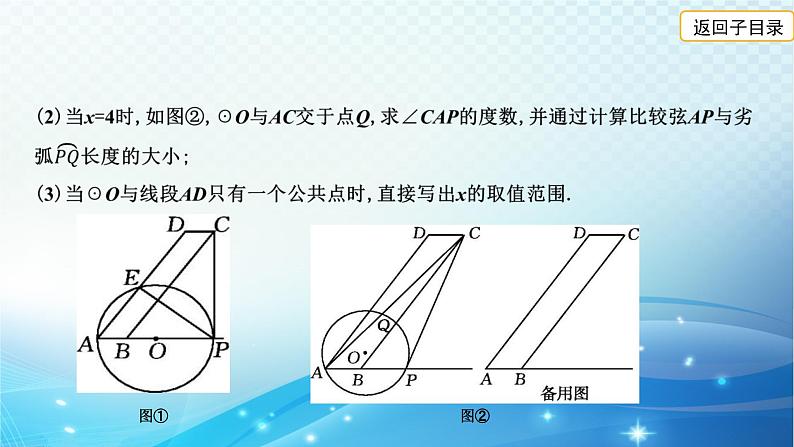
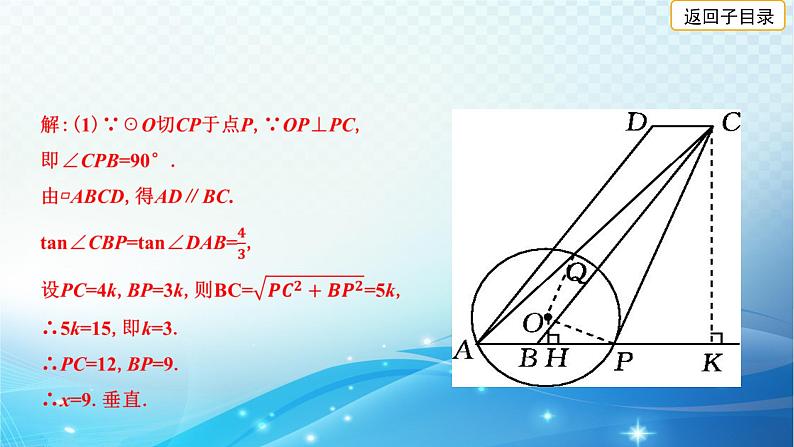
(2)如图,连接OP,OQ,作CK⊥AB于点K,OH⊥AP于点H,同(1)法得CK=12.
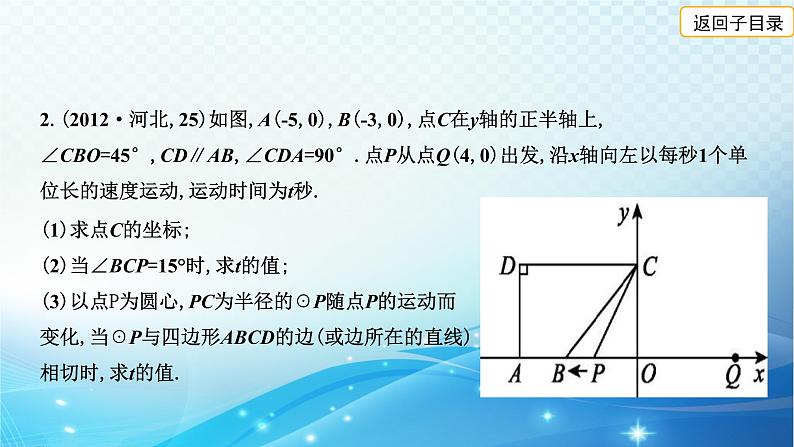
2.(2012·河北,25)如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长的速度运动,运动时间为t秒.
(1)求点C的坐标;(2)当∠BCP=15°时,求t的值;(3)以点P为圆心,PC为半径的☉P随点P的运动而变化,当☉P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
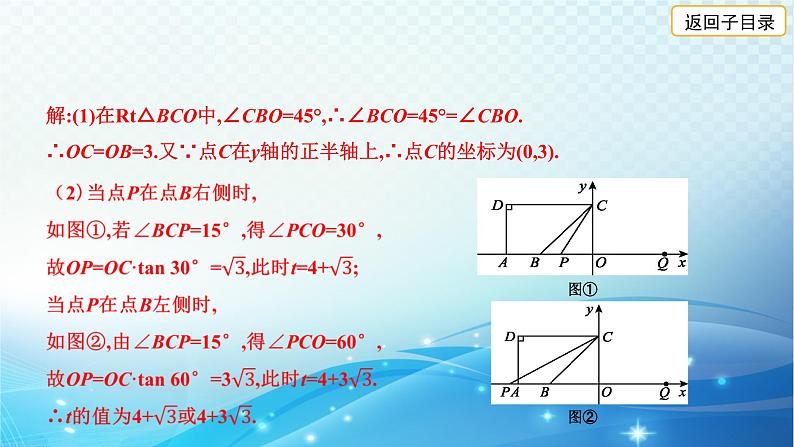
解:(1)在Rt△BCO中,∠CBO=45°,∴∠BCO=45°=∠CBO.∴OC=OB=3.又∵点C在y轴的正半轴上,∴点C的坐标为(0,3).
(3)由题意知,若☉P与四边形ABCD的边相切,有以下三种情况:①当☉P与BC相切于点C时,有∠BCP=90°,从而∠OCP=45°,得到OP=3,此时t=1;②当☉P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4;③当☉P与AD相切时,由题意,得∠DAO=90°,故点A为切点,如图③所示, PC2=PA2=(9-t)2,PO2=(t-4)2,于是(9-t)2=(t-4)2+32,解得t=5.6.∴t的值为1或4或5.6.
(3)设点M为Rt△APO的外心,则M为OA的中点,∴OM=4.∵当点M在扇形的内部时,OM(3)10°或170°.
6.(2020·河北,14)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC,如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑得不周全,∠A还应有另一个不同的值.”下列判断正确的是（ ）
A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值
7.(2016·河北,9)如图为4×4的网格图,A,B,C,D,O均在格点上,点O是(　　)
A.△ACD的外心B.△ABC的外心 C.△ACD的内心 D.△ABC的内心
8.(2015·河北,6)如图,AC,BE是☉O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是 (　　)
A.△ABE B.△ACF C.△ABD D.△ADE
(1)点在圆外⇔④　　　　; (2)点在圆上⇔d=r;(3)点在圆内⇔⑤　　　　. 
1.点和圆的位置关系有三种,分别是①　　　　 、②　　　　 和③　　　 　. 
2.设圆的半径为r,圆所在平面上任一点到圆心的距离为d,如图,则:
设圆的半径为r,圆心到直线的距离为d.
1.性质:圆的切线⑧　　　　于过切点的半径.2.判定(1)经过半径的外端并且⑨　　　　于这条半径的直线是圆的切线. (2)圆心到直线的距离⑩　　　　半径,则直线是圆的切线. (3)和圆只有⑪　　　　公共点的直线是圆的切线.
3.切线长定理(1)定义:经过圆外一点作圆的一条切线,这一点和切点之间线段的长叫做这点到圆的切线长.(2)定理:从圆外一点可以引圆的两条切线,它们的切线长 　　　　,这一点和圆心的连线 　　　　两条切线的夹角.如图,已知PA,PB与☉O分别相切于A,B,则PA=PB,PO平分∠APB. 
1.外接圆(1)定义:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,如图所示,外接圆的圆心是三角形三条边的垂直平分线的交点,外接圆的圆心叫做这个三角形的外心.
(2)性质:三角形的外心到三角形三个顶点的距离相等.
2.内切圆(1)定义:与三角形各边都相切的圆叫做三角形的内切圆,如图所示,内切圆的圆心是三角形三条角平分线的交点,内切圆的圆心叫做三角形的内心. (2)性质:三角形内切圆的圆心到三角形三边的距离相等.
A.当a=-1时,点B在☉A上 B.当a<1时,点B在☉A内C.当a<-1时,点B在☉A外 D.当-1(2021·河北模拟)在平面直角坐标系内,点A的坐标为(1,0),点B的坐标为(a,0),☉A的半径为2.下列说法中不正确的是(　　)
2. (2021·保定模拟) 如图,在△ABC中,AB=3,AC=4,BC=5,点D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是 (　　)
A.相切　 　B.相交 　　C.相离　 　D.无法确定
3.(2021·原创题)如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作☉P.当☉P与正方形ABCD的边相切时,BP的长为 (　　)
5.(2021·保定一模)如图,在平行四边形ABCD中,AB=10,AD=m,∠D=60°,以AB为直径作☉O.
(1)求圆心O到BC的距离;(2)求圆心O到CD的距离(用含m的代数式来表示);(3)当m取何值时,CD与☉O相切;(4)当m取何值时,CD与圆有两个交点.
1. (2021·河北三市联考)如图PA,PB分别与☉O相切于点A,B,点C为☉O上一点,∠P=66°,则∠C= (　　)
A.57° B.60° C.63° D.66°
2. (2021·河北中考压轴卷)如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点A为60°角与直尺交点,点B为光盘与直尺唯一交点,若AB=3,则光盘的直径是 (　　)
3. (2021·邯郸质量检测)如图,☉O的直径AB=4,BC切☉O于点B,OC平行于弦AD,OC=5,则AD的长为 (　　)
4. (2021·河北预测)如图,有两个同心圆,PA切小圆于点A,PB切大圆于点B,若PA=3 cm,PB=2 cm,那么两个圆所围成的圆环的面积为(　　)
A.1 cm2 B.5 cm2 C.π cm2 D.5π cm2
5. (2021·河北预测)如图,在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC为直径作☉O交AB于点D.
(1)求线段AD的长度;(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与☉O相切?请说明理由
(2)当点E是AC的中点时,ED与☉O相切.理由如下:如图,连接OD.∵DE是Rt△ADC的中线,∴ED=EC,∴∠EDC=∠ECD.∵OC=OD,∴∠ODC=∠OCD,∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°,　∴ED⊥OD.∴ED与☉O相切.
(1)求证:直线BF是☉O的切线;(2)若OB=2,求BD的长.
1.(2021·河北模拟)如图所示,在△ABC中,∠BIC=125°,点I是内心,点O是外心,则∠BOC等于(　　)
A.130° B.135° C.140° D.145°
2.(2021·河北模拟)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的大小为(　　)
A.64° B.120° C.122° D.128°
4. (2021·邯郸模拟)已知点O是△ABC的外心,连接AO并延长交BC于点D.若∠B=40°,∠BAD=22°,则∠C的度数为 (　　)
A.52° B.58° C.62° D.68°
6.(2021·河北预测)如图,以△ABC的边AC为直径的☉O恰为△ABC的外接圆,∠ABC的平分线交☉O于点D,过点D作DE∥AC交BC的延长线于点E.
解:(1)证明:如图,连接OD.∵AC是☉O的直径,∴∠ABC=90°.∵BD平分∠ABC,∴∠ABD=45°.∴∠AOD=90°.∵DE∥AC,∴∠ODE=∠AOD=90°,即OD⊥DE.∴DE是☉O的切线.