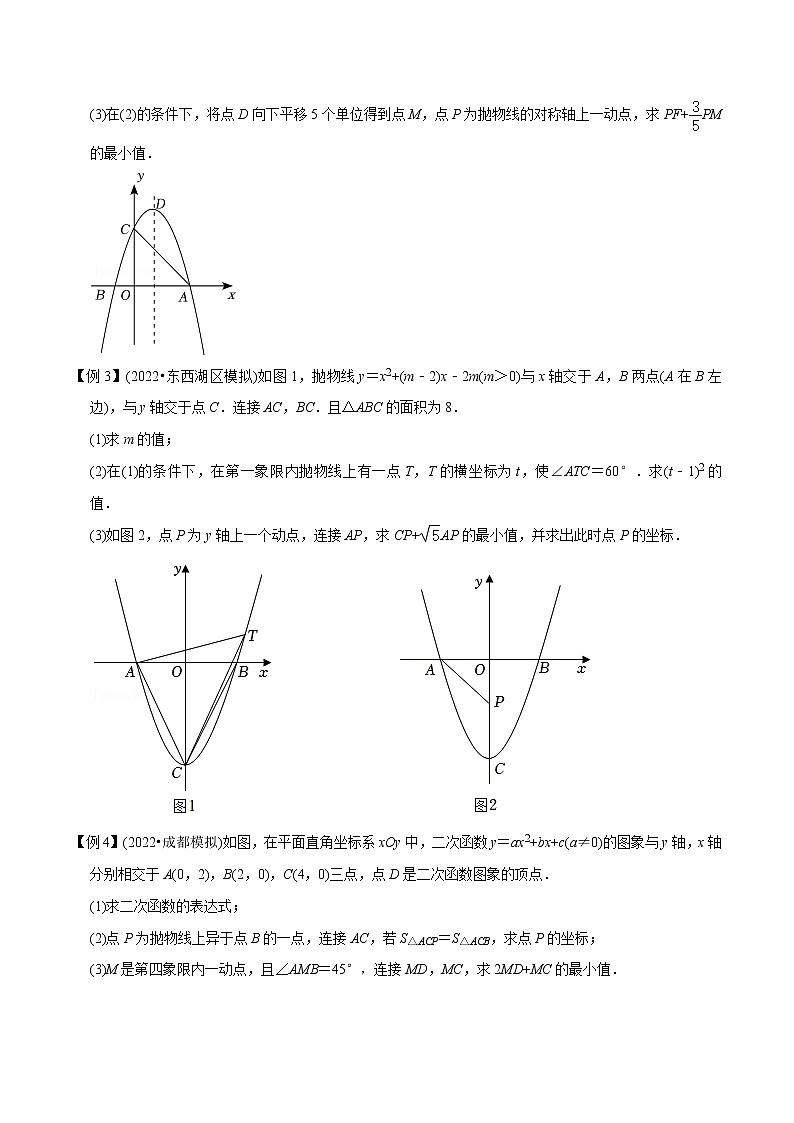
专题13二次函数与胡不归型最值问题-挑战2023年中考数学压轴题之学霸秘笈大揭秘（学生版）

挑战2023年中考数学压轴题之学霸秘笈大揭秘(全国通用)

              专题13二次函数与胡不归型最值问题

胡不归问题：

模型分析：“PA＋k·PB”型的最值问题，当k＝1时通常为轴对称之最短路径问题，而当k＞0时，若以常规的轴对称的方式解决，则无法进行，因此必须转换思路．

如图，直线BM，BN交于点B，P为BM上的动点，点A在射线BM，BN同侧，已知sin∠MBN＝k．

过点A作AC⊥BN于点C，交BM于点P，此时PA＋k·PB取最小值，最小值即为AC的长．

证明  如图，在BM上任取一点Q，连结AQ，作QD⊥BN于点D．

由sin∠MBN＝k，可得QD＝ k·QB．

所以QA＋k·QB＝QA＋QD≥AC，即得证．

【例1】(2022•济南)抛物线y＝ax2+x﹣6与x轴交于A(t，0)，B(8，0)两点，与y轴交于点C，直线y＝kx﹣6经过点B．点P在抛物线上，设点P的横坐标为m．

(1)求抛物线的表达式和t，k的值；

(2)如图1，连接AC，AP，PC，若△APC是以CP为斜边的直角三角形，求点P的坐标；

(3)如图2，若点P在直线BC上方的抛物线上，过点P作PQ⊥BC，垂足为Q，求CQ+PQ的最大值．

【例2】(2022•宜宾)如图，抛物线y＝ax2+bx+c与x轴交于A(3，0)、B(﹣1，0)两点，与y轴交于点C(0，3)，其顶点为点D，连结AC．

(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标；

(2)在抛物线的对称轴上取一点E，点F为抛物线上一动点，使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形，求点F的坐标；

(3)在(2)的条件下，将点D向下平移5个单位得到点M，点P为抛物线的对称轴上一动点，求PF+PM的最小值．

【例3】(2022•东西湖区模拟)如图1，抛物线y＝x2+(m﹣2)x﹣2m(m＞0)与x轴交于A，B两点(A在B左边)，与y轴交于点C．连接AC，BC．且△ABC的面积为8．

(1)求m的值；

(2)在(1)的条件下，在第一象限内抛物线上有一点T，T的横坐标为t，使∠ATC＝60°．求(t﹣1)2的值．

(3)如图2，点P为y轴上一个动点，连接AP，求CP+AP的最小值，并求出此时点P的坐标．

【例4】(2022•成都模拟)如图，在平面直角坐标系xOy中，二次函数y＝ax2+bx+c(a≠0)的图象与y轴，x轴分别相交于A(0，2)，B(2，0)，C(4，0)三点，点D是二次函数图象的顶点．

(1)求二次函数的表达式；

(2)点P为抛物线上异于点B的一点，连接AC，若S△ACP＝S△ACB，求点P的坐标；

(3)M是第四象限内一动点，且∠AMB＝45°，连接MD，MC，求2MD+MC的最小值．

1．(2022•河北区二模)已知抛物线y＝﹣x2+bx+c(b，c为常数)的图象与x轴交于A(1，0)，B两点(点A在点B左侧)．与y轴相交于点C，顶点为D．

(Ⅰ)当b＝2时，求抛物线的顶点坐标；

(Ⅱ)若点P是y轴上一点，连接BP，当PB＝PC，OP＝2时，求b的值；

(Ⅲ)若抛物线与x轴另一个交点B的坐标为(4，0)，对称轴交x轴于点E，点Q是线段DE上一点，点N为线段AB上一点，且AN＝2BN，连接NQ，求DQ+NQ的最小值．

2．(2021•南海区二模)如图1，抛物线y＝x2+bx+c与x轴交于A、B两点，点A、B分别位于原点左、右两侧，且AO＝2BO＝4，过A点的直线y＝kx+c交y轴于点C．

(1)求k、b、c的值；

(2)在抛物线的对称轴上是否存在一点P，使△ACP为直角三角形？若存在，直接写出所有满足条件的点的坐标；若不存在，请说明理由；

(3)如图2，点M为线段AC上一点，连接OM，求AM+OM的最小值．

3．(2021•宝安区模拟)(1)已知二次函数经过点A(﹣3，0)、B(1，0)、C(0，3)，请求该抛物线解析式；

(2)点M为抛物线上第二象限内一动点，BM交y轴于点N，当BM将四边形ABCM的面积分为1：2两部分时，求点M的坐标；

(3)点P为对称轴上D点下方一动点，点Q为直线y＝x第一象限上的动点，且DP＝OQ，求BP+BQ的最小值并求此时点P的坐标．

4．(2021•南沙区一模)已知，抛物线y＝mx2+x﹣4m与x轴交于点A(﹣4，0)和点B，与y轴交于点C．点D(n，0)为x轴上一动点，且有﹣4＜n＜0，过点D作直线l⊥x轴，且与直线AC交于点M，与抛物线交于点N，过点N作NP⊥AC于点P．点E在第三象限内，且有OE＝OD．

(1)求m的值和直线AC的解析式．

(2)若点D在运动过程中，AD+CD取得最小值时，求此时n的值．

(3)若△ADM的周长与△MNP的周长的比为5：6时，求AE+CE的最小值．

5．(2021•射阳县三模)如图，抛物线y＝ax2+bx+c经过A(﹣1，0)、B(3，0)、C(0，3)三点，对称轴与抛物线相交于点P，与直线BC相交于点M，连接AC，PB．

(1)求该抛物线的解析式；

(2)设对称轴与x轴交于点N，在对称轴上是否存在点G，使以O、N、G为顶点的三角形与△AOC相似？如果存在，请求出点G的坐标；如果不存在，请说明理由；

(3)抛物线上是否存在一点Q，使△QMB与△PMB的面积相等，若存在，求点Q的坐标；若不存在，请说明理由；

(4)点E是y轴上的动点，连接ME，求ME+CE的最小值．

6．(2021•深圳模拟)如图1，抛物线y＝﹣x2+bx+c交x轴于A、B两点，其中点A坐标为(﹣3，0)，与y轴交于点C(0，3)，点D为抛物线y＝﹣x2+bx+c的顶点．

(1)求抛物线的函数表达式；

(2)若点E在x轴上，且∠ECA＝∠CAD，求点E的坐标；

(3)如图2，点P为线段AC上方的抛物线上任一点，过点P作PH⊥x轴于点H，与AC交于点M．

①求△APC的面积最大时点P的坐标；

②在①的条件下，若点N为y轴上一动点，求HN+CN的最小值．

7．(2021•深圳模拟)已知：如图，点A(1，0)，B(3，0)，D(2，﹣1)，C是y轴上的点，且OC＝3．

(1)过点A作AM⊥BC，垂足为M，连接AD、BD，求证：四边形ADBM为正方形；

(2)若过A、B、C三点的抛物线对称轴上有一动点P，当PC﹣PB的值最大时，求出点P的坐标；

(3)设Q为线段OC上的一动点，问：AQ+QC是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

8．(2021•资阳)抛物线y＝﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，且B(﹣1，0)，C(0，3)．

(1)求抛物线的解析式；

(2)如图1，点P是抛物线上位于直线AC上方的一点，BP与AC相交于点E，当PE：BE＝1：2时，求点P的坐标；

(3)如图2，点D是抛物线的顶点，将抛物线沿CD方向平移，使点D落在点D'处，且DD'＝2CD，点M是平移后所得抛物线上位于D'左侧的一点，MN∥y轴交直线OD'于点N，连结CN．当D'N+CN的值最小时，求MN的长．

9．(2022•杜尔伯特县一模)如图，已知抛物线y＝x2+bx+c与x轴相交于A(﹣1，0)，B(m，0)两点，与y轴相交于点C(0，﹣3)，抛物线的顶点为D．

(1)求抛物线的解析式；

(2)若点E在x轴上，且∠ECB＝∠CBD，求点E的坐标．

(3)若P是直线BC下方抛物线上任意一点，过点P作PH⊥x轴于点H，与BC交于点M．

①求线段PM长度的最大值．

②在①的条件下，若F为y轴上一动点，求PH+HF+CF的最小值．

10．(2020•自贡)在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A(﹣3，0)、B(1，0)，交y轴于点N，点M为抛物线的顶点，对称轴与x轴交于点C．

(1)求抛物线的解析式；

(2)如图1，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：

①求PD+PC的最小值；

②如图2，Q点为y轴上一动点，请直接写出DQ+OQ的最小值．

11．(2022•中山市三模)如图，抛物线y＝ax2+bx﹣3与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴为直线x＝1，点A(﹣1，0)，过B的直线交y轴于点D，交抛物线于E，且．

(1)求抛物线的解析式；

(2)在抛物线第四象限的图象上找一点P，使得△BDP的面积最大，求出点P的坐标；

(3)点M是线段BE上的一点，求的最小值，并求出此时点M的坐标．

12．(2021•南山区校级三模)如图，已知抛物线y＝ax2+bx+c(a≠0)与y轴相交于点C(0，﹣2)，与x轴分别交于点B(3，0)和点A，且tan∠CAO＝1．

(1)求抛物线解析式．

(2)抛物线上是否存在一点Q，使得∠BAQ＝∠ABC，若存在，请求出点Q坐标，若不存在，请说明理由；

(3)抛物线的对称轴交x轴于点D，在y轴上是否存在一个点P，使PC+PD值最小，若存在，请求出最小值，若不存在，请说明理由．

13．(2021•津南区一模)已知抛物线y＝x2﹣2x+c交x轴于A，B两点，且点B的坐标为(3，0)，其对称轴交x轴于点C．

(Ⅰ)求该抛物线的顶点D的坐标；

(Ⅱ)设P是线段CD上的一个动点(点P不与点C，D重合)．

①过点P作y轴的垂线l交抛物线(对称轴右侧)于点Q，连接QB，QD，求△QBD面积的最大值；

②连接PB，求PD+PB的最小值．

14．(2021•防城区模拟)如图，已知抛物线y＝ax2﹣2ax﹣8a(a＞0)与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y＝﹣x+与抛物线的另一交点为D，且点D的横坐标为﹣5．

(1)求抛物线的函数表达式；

(2)若点P(x，y)在该二次函数的图象上，且S△BCD＝S△ABP，求点P的坐标；

(3)设F为线段BD上的一个动点(异于点B和D)，连接AF．是否存在点F，使得2AF+DF的值最小？若存在，分别求出2AF+DF的最小值和点F的坐标，若不存在，请说明理由．

15．(2021秋•沈北新区校级月考)如图，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2﹣2x+c与x轴交于点A(1，0)，点B(﹣3，0)，与y轴交于点C，连接BC，点P在第二象限的抛物线上，连接PC、PO，线段PO交线段BC于点E．

(1)求抛物线的表达式；

(2)若△PCE的面积为S1，△OCE的面积为S2，当＝时，求点P的坐标；

(3)已知点C关于抛物线对称轴的对称点为点N，连接BN，点H在x轴上，当∠HCB＝∠NBC时，

①求满足条件的所有点H的坐标；

②当点H在线段AB上时，平面内点M，且HM＝1，直接写出AM+CM的最小值．

16．(2021•香洲区校级三模)如图，抛物线y＝﹣x2﹣6x+7交x轴于A，B两点(点A在点B左侧)，交y轴于点C，直线y＝x+7经过点A、C，点M是线段AC上的一动点(不与点A，C重合)．

(1)求A，B两点的坐标；

(2)当点P，C关于抛物线的对称轴对称时，求PM+AM的最小值及此时点M的坐标；

(3)连接BC，当△AOM与△ABC相似时，求出点M的坐标．

17．(2021•涪城区校级模拟)已知：如图所示，抛物线y＝﹣x2﹣x+c与x轴交于A、B两点，与y轴的正半轴交于点C，点A在点B的左侧，且满足tan∠CAB•tan∠CBA＝1．

(1)求A、B两点的坐标；

(2)若点P是抛物线y＝﹣x2﹣x+c上一点，且△PAC的内切圆的圆心正好落在x轴上，求点P的坐标；

(3)若M为线段AO上任意一点，求MC+AM的最小值．

18．(2021•青山区模拟)已知抛物线y＝ax2﹣4ax﹣12a与x轴相交于A，B两点，与y轴交于C点，且OC＝OA．设抛物线的顶点为M，对称轴交x轴于点N．

(1)求抛物线的解析式；

(2)如图1，点E(m，n)为抛物线上的一点，且0＜m＜6，连接AE，交对称轴于点P．点F为线段BC上一动点，连接EF，当PA＝2PE时，求EF+BF的最小值．

(3)如图2，过点M作MQ⊥CM，交x轴于点Q，将线段CQ向上平移t个单位长度，使得线段CQ与抛物线有两个交点，求t的取值范围．

19．(2021•罗湖区校级模拟)已知抛物线y＝ax2+bx(a，b为常数，a≠0)与x轴的正半轴交于点A，其顶点C的坐标为(2，4)．

(Ⅰ)求抛物线的解析式；

(Ⅱ)点P是抛物线上位于直线AC上方的一个动点，求△PAC面积的最大值；

(Ⅲ)点Q是抛物线对称轴上的一个动点，连接QA，求QC+QA的最小值．

20．(2020•东胜区二模)如图，在平面直角坐标系中，二次函数y＝ax2+bx+c的图象经过点A(﹣2，0)，B(0，)，C(1，0)，其对称轴与x轴交于点E，顶点坐标为D．

(1)求二次函数的表达式；

(2)点P为抛物线的对称轴上的一个动点，且在第二象限内，若平面内存在点Q，使得以B，C，P，Q为顶点的四边形为菱形，求点Q的坐标；

(3)若M为y轴上的一个动点，连接ME，求MB+ME的最小值．